Robust estimators (Robust estimators)
I just want to apologize, I learned about robust estimators from the English-language literature, so some terms are direct from English, it may well be that in the Russian-language literature the topic of robust assessments has some kind of steady momentum.
While studying at the university, the course of statistics, which was read to us (and this was more than 15 years ago), was the most typical one: introduction through probability theory and frequently encountered distributions. More in the head since then about this semester course nothing is left. It seems to me that in the course of statistical physics, much is given much better. Much later, life confronted me with medical physics, where statistical methods are one of the main tools for analyzing data obtained, for example, using NMR tomography. This is the first time I met the term robust statistics and robust estimators. Immediately make a reservation, I will show only simple examples of the use of robust estimators and give references to literature, those interested can easily deepen and expand their knowledge using the list of references at the end of this note. Let's analyze the simplest example most often encountered in order to demonstrate a reliable estimate in any sample. Suppose student Vasya is sitting on a physical workshop and is recording the readings of a certain instrument:
')
4.5
4.1
5.2
5.5
3.9
4.3
5.7
6.0
45
47
The device does not work very accurately, plus Vasya is distracted by conversations with her practical neighbor, Lena. As a result, in the last two entries, Vasily does not put a decimal point and, voila, we have a problem.
Step one, we order our sample in ascending order and calculate the average
mean = 13.12
It is immediately evident that the average value is far from the real average due to the last two outliers (outliers) that are in the sample. The easiest way to estimate the average of ignoring emissions is the median
median = 5.35
Thus, the simplest robust estimator is the median; indeed, we can see that up to 50% of the data can be “polluted” by various kinds of emissions, but the median estimate will not change. In this simple example, you can enter several concepts at once: what is robustness in statistics (stability of estimates with respect to emissions in the data), how used estimator is robust (how much data can be “polluted” without a significant change in the obtained estimates) [1]. Can the median score be improved? Of course, you can enter a more reliable estimator known as absolute deviation from the median (median absolute deviation or MAD)
MAD = median (| xi-median [xj] |)
in the case of a normal distribution, a numerical factor is introduced in front of the MAD, allowing the estimate to be kept unchanged. As it is easy to see the stability of the MAD is also 50%.
Robust estimators have found tremendous practical application in linear regressions. In the case of a linear relationship (x, y), it is often necessary to obtain well-defined estimates of such a relationship (often in the case of multivariate regression)
y = Bx + E ,
where B can already be a matrix of coefficients, E is some noise spoiling our measurements, and x is a set of parameters (vector), which we actually want to estimate using measured values of y (vector). The easiest and well-known way to do this is the least squares method (OLS) [2]. In principle, it is very easy to make sure that the OLS is not a robust estimator and its robust reliability is 0%, since even one outlier can significantly change the estimate. One of the most mathematical beautiful tricks to improve the score is called least trimmed squares or the method of “trimmed” squares (MUK). His idea is to trivially modify the original OLS, in which the number of evaluations used is trimmed, ie:
original MNC
MUK
where r_i are already ordered estimation errors (y - O (x)) , i.e. r_1 <r_2 <... <r_N . Again, it is easy to verify that the minimum truncating factor that allows a reliable estimate of h = N / 2 + p ( p is the number of independent variables plus one), i.e. Reliability robust estimates again can be almost 50%. Actually, with the MUK, everything is quite simple, except for one nontrivial question related to the choice of h . The first sighting method of choice can be characterized as “by eye”. If the sample where we are regressing is not very large, then the number of outliers can be estimated and the trimming factor should be chosen by trying several close values, especially if the estimate does not change with decreasing / increasing. However, there are more stringent selection criteria [3,4], which, unfortunately, lead to a noticeable increase in the counting time even in the case of linear regressions.
We will enumerate other known estimators, which are often used in the literature [1]:
1) least median squares (median squares method)
2) M-, R-, S-, Q- estimators, estimators based on some evaluation function (for example, the OLS can also be called the M-estimator), and
various variations of error estimates (moments, cutting hyperplanes, etc.).
3) Estimators for nonlinear regressions [5]
Point two on this list is somewhat inaccurate, because for convenience, many estimators that are quite different in nature are collected in one heap.
As a simple but very interesting application of robust estimates, we give a robust estimate of the diffusion tensor in NMR tomography [6]. In NMR tomography, one of the interesting applications is diffusion measurements on water molecules that are subject to Brownian motion in the brain. However, due to various restrictions (movement along neurofibers, in dendrides, inside and outside cells, etc.) have different diffusion parameters. By measuring in six different directions (the diffusion tensor is positively defined, that is, we need to know only 6 of its elements), we can recover the tensor itself, through the well-known model of the signal decay. Spatial directions are encoded by gradient coils in a pulse sequence. We can imagine a diffusion tensor as an ellipsoid, get an image of the neural threads in the brain (see for example diffusion MRI in the wiki
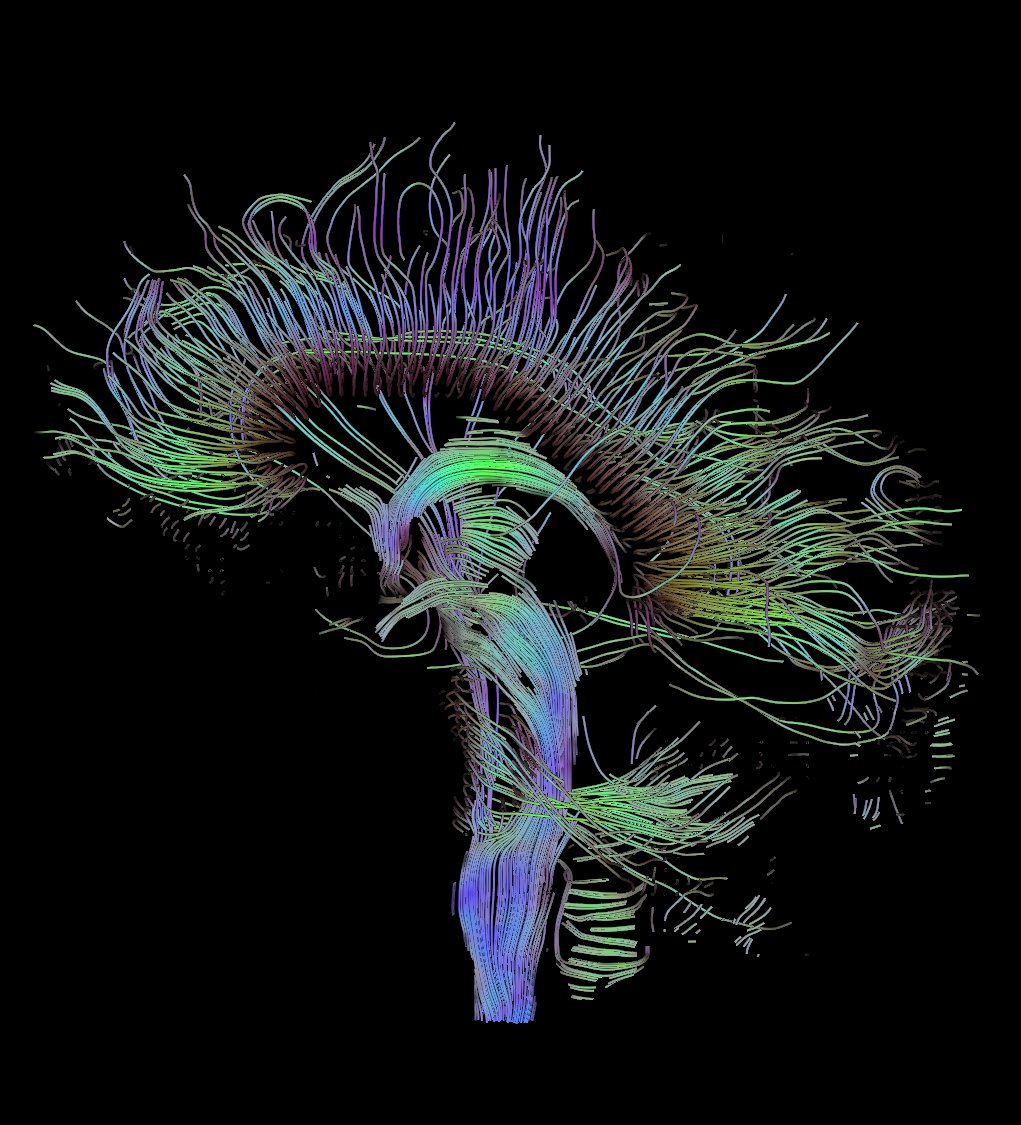
). The threads are ordered tensors, which are approximated by a certain curve (through the well-known Runge-Kutta method). This approach is called streamline [7].
However, measurements of this kind are richest in various kinds of artifacts (compared to other types of images) because of the heartbeat, the respiratory movement of the chest, the movement of the head during measurements, different ticks, table shake due to often switching magnetic gradients, etc. . Thus, the restored diffusion tensor can have noticeable deviations from the real values and, as a result, the wrong direction in the case of its pronounced anisotropy. It does not allow to use the obtained tracks of nerve fibers as a reliable source of information about the structure of nerve connections or to plan surgeries. In fact, the approach based on the diffusion tensor is not used to restore the image of nerve fibers, so most patients can not worry yet.
The mathematical theory of robust estimators is quite interesting, since in many cases, it is based on already known approaches (this means that most of the strict and dry theory is already known), but it has additional properties that allow to significantly complement and improve the estimated results. If we return to the OLS already mentioned, the introduction of weighting factors allows us to obtain robust estimates in the case of linear regression. The next step is to change the weight factors by introducing iterations in the estimates, in the end we get the well-known iteratively reweighted least squares approach [2].
Hopefully, readers unfamiliar with robust statistics have gained some insight into robust estimators, and acquaintances have seen interesting applications of their knowledge.
Literature
1. Rousseeuw PJ, Leroy AM, Robust regression and outlier detection. Wiley, 2003.
2. Bjoerck A, Numerical methods for least squares problems. SIAM, 1996.
3. Agullo, J. New algorithm for computing the least trimmed squares regression estimator. Computational statistics & data analysis 36 (2001) 425-439.
4. Hofmann M, Gatu C, Kontoghiorghes EJ. Analogue trimmed squares algorithm for a range of coverage values. Journal of computational and graphical statistics 19 (2010) 191-204.
5. Motulsky HJ, Brown RE. Nonlinear Regression Detecting outliers when fitting out. BMC Bioinfromatics 7 (2006) 123.
6. Change LC, Jones DK, Pierpaoli C. RESTORE: Robust estimation of tensors by oulier rejection. Magnetic Resonance in Medicine 53 (2005) 1088-1085.
7. Jones DK, Diffusion MRI: Theory, Methods and Applications. Oxford University Press, 2010.
While studying at the university, the course of statistics, which was read to us (and this was more than 15 years ago), was the most typical one: introduction through probability theory and frequently encountered distributions. More in the head since then about this semester course nothing is left. It seems to me that in the course of statistical physics, much is given much better. Much later, life confronted me with medical physics, where statistical methods are one of the main tools for analyzing data obtained, for example, using NMR tomography. This is the first time I met the term robust statistics and robust estimators. Immediately make a reservation, I will show only simple examples of the use of robust estimators and give references to literature, those interested can easily deepen and expand their knowledge using the list of references at the end of this note. Let's analyze the simplest example most often encountered in order to demonstrate a reliable estimate in any sample. Suppose student Vasya is sitting on a physical workshop and is recording the readings of a certain instrument:
')
4.5
4.1
5.2
5.5
3.9
4.3
5.7
6.0
45
47
The device does not work very accurately, plus Vasya is distracted by conversations with her practical neighbor, Lena. As a result, in the last two entries, Vasily does not put a decimal point and, voila, we have a problem.
Step one, we order our sample in ascending order and calculate the average
mean = 13.12
It is immediately evident that the average value is far from the real average due to the last two outliers (outliers) that are in the sample. The easiest way to estimate the average of ignoring emissions is the median
median = 5.35
Thus, the simplest robust estimator is the median; indeed, we can see that up to 50% of the data can be “polluted” by various kinds of emissions, but the median estimate will not change. In this simple example, you can enter several concepts at once: what is robustness in statistics (stability of estimates with respect to emissions in the data), how used estimator is robust (how much data can be “polluted” without a significant change in the obtained estimates) [1]. Can the median score be improved? Of course, you can enter a more reliable estimator known as absolute deviation from the median (median absolute deviation or MAD)
MAD = median (| xi-median [xj] |)
in the case of a normal distribution, a numerical factor is introduced in front of the MAD, allowing the estimate to be kept unchanged. As it is easy to see the stability of the MAD is also 50%.
Robust estimators have found tremendous practical application in linear regressions. In the case of a linear relationship (x, y), it is often necessary to obtain well-defined estimates of such a relationship (often in the case of multivariate regression)
y = Bx + E ,
where B can already be a matrix of coefficients, E is some noise spoiling our measurements, and x is a set of parameters (vector), which we actually want to estimate using measured values of y (vector). The easiest and well-known way to do this is the least squares method (OLS) [2]. In principle, it is very easy to make sure that the OLS is not a robust estimator and its robust reliability is 0%, since even one outlier can significantly change the estimate. One of the most mathematical beautiful tricks to improve the score is called least trimmed squares or the method of “trimmed” squares (MUK). His idea is to trivially modify the original OLS, in which the number of evaluations used is trimmed, ie:
original MNC
min \sum_{i=1}^N r_i^2, MUK
min \sum_{i=1}^h {r_i^2}_{1:N}, where r_i are already ordered estimation errors (y - O (x)) , i.e. r_1 <r_2 <... <r_N . Again, it is easy to verify that the minimum truncating factor that allows a reliable estimate of h = N / 2 + p ( p is the number of independent variables plus one), i.e. Reliability robust estimates again can be almost 50%. Actually, with the MUK, everything is quite simple, except for one nontrivial question related to the choice of h . The first sighting method of choice can be characterized as “by eye”. If the sample where we are regressing is not very large, then the number of outliers can be estimated and the trimming factor should be chosen by trying several close values, especially if the estimate does not change with decreasing / increasing. However, there are more stringent selection criteria [3,4], which, unfortunately, lead to a noticeable increase in the counting time even in the case of linear regressions.
We will enumerate other known estimators, which are often used in the literature [1]:
1) least median squares (median squares method)
min median r_i^2 2) M-, R-, S-, Q- estimators, estimators based on some evaluation function (for example, the OLS can also be called the M-estimator), and
various variations of error estimates (moments, cutting hyperplanes, etc.).
3) Estimators for nonlinear regressions [5]
Point two on this list is somewhat inaccurate, because for convenience, many estimators that are quite different in nature are collected in one heap.
As a simple but very interesting application of robust estimates, we give a robust estimate of the diffusion tensor in NMR tomography [6]. In NMR tomography, one of the interesting applications is diffusion measurements on water molecules that are subject to Brownian motion in the brain. However, due to various restrictions (movement along neurofibers, in dendrides, inside and outside cells, etc.) have different diffusion parameters. By measuring in six different directions (the diffusion tensor is positively defined, that is, we need to know only 6 of its elements), we can recover the tensor itself, through the well-known model of the signal decay. Spatial directions are encoded by gradient coils in a pulse sequence. We can imagine a diffusion tensor as an ellipsoid, get an image of the neural threads in the brain (see for example diffusion MRI in the wiki

). The threads are ordered tensors, which are approximated by a certain curve (through the well-known Runge-Kutta method). This approach is called streamline [7].
However, measurements of this kind are richest in various kinds of artifacts (compared to other types of images) because of the heartbeat, the respiratory movement of the chest, the movement of the head during measurements, different ticks, table shake due to often switching magnetic gradients, etc. . Thus, the restored diffusion tensor can have noticeable deviations from the real values and, as a result, the wrong direction in the case of its pronounced anisotropy. It does not allow to use the obtained tracks of nerve fibers as a reliable source of information about the structure of nerve connections or to plan surgeries. In fact, the approach based on the diffusion tensor is not used to restore the image of nerve fibers, so most patients can not worry yet.
The mathematical theory of robust estimators is quite interesting, since in many cases, it is based on already known approaches (this means that most of the strict and dry theory is already known), but it has additional properties that allow to significantly complement and improve the estimated results. If we return to the OLS already mentioned, the introduction of weighting factors allows us to obtain robust estimates in the case of linear regression. The next step is to change the weight factors by introducing iterations in the estimates, in the end we get the well-known iteratively reweighted least squares approach [2].
Hopefully, readers unfamiliar with robust statistics have gained some insight into robust estimators, and acquaintances have seen interesting applications of their knowledge.
Literature
1. Rousseeuw PJ, Leroy AM, Robust regression and outlier detection. Wiley, 2003.
2. Bjoerck A, Numerical methods for least squares problems. SIAM, 1996.
3. Agullo, J. New algorithm for computing the least trimmed squares regression estimator. Computational statistics & data analysis 36 (2001) 425-439.
4. Hofmann M, Gatu C, Kontoghiorghes EJ. Analogue trimmed squares algorithm for a range of coverage values. Journal of computational and graphical statistics 19 (2010) 191-204.
5. Motulsky HJ, Brown RE. Nonlinear Regression Detecting outliers when fitting out. BMC Bioinfromatics 7 (2006) 123.
6. Change LC, Jones DK, Pierpaoli C. RESTORE: Robust estimation of tensors by oulier rejection. Magnetic Resonance in Medicine 53 (2005) 1088-1085.
7. Jones DK, Diffusion MRI: Theory, Methods and Applications. Oxford University Press, 2010.
Source: https://habr.com/ru/post/174705/
All Articles