RE: Is time travel possible?
Yesterday on Habré appeared a stunning post illiteracy " Is it possible to travel in time ." In response to my remark about being unfamiliar with basic scientific ideas about space and time, the author attached me like this:
I have not seen such a level of militant ignorance for a long time, and it’s doubly strange to see him on Habré.
Since I, unlike the author, are a scientist , I will try in response to tell the inquisitive reader what we really know about the nature of time, causality, and time travel.
')
In classical mechanics, time is considered absolute and unchanged in the sense that when moving from one reference system to another, the time intervals do not change:
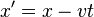



Here (x, y, z, t) are the coordinates in the old system, (x ', y', z ', t') are the coordinates in the new system. Hereinafter, it is assumed (to simplify the formulas) that one system moves relative to another parallel to the x axis with velocity v.
This is the so-called. Galilean transformations - what happens to the coordinates when changing the reference system. In the Galilean sense, the “flow of time” is one for the whole Universe, and the temporal coordinates of all objects are the same. In this case, classical mechanics does not interpret the uniqueness of the arrow of time; moreover, the very concept of the movement of time is not included in the Newton formulas in any way.
In classical mechanics, we ourselves introduce movement from the past to the future. Suppose we have a set of material points (coordinates and velocities) and acting forces. Next, we ask some interval dt and see how the system will evolve over time. No one prevents us from moving in the opposite direction and follow what happened to the system in the past.
However, “time travel” - i.e. the movement of one particular object on the scale t to the past - by Newtonian mechanics is forbidden (see above - the time flow is one for the whole Universe).
The situation became much more fun when Maxwell formulated his electrodynamics, and then Einstein, trying to solve the contradictions of electrodynamics and classical mechanics, created the theory of relativity.
In the framework of the special theory of relativity, in the transition from one inertial frame of reference to another, we already use such transformations:
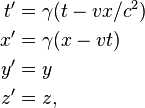 ,
,
Where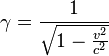 .
.
Here, as is easy to see, each frame of reference has its own time scale. In the framework of the SRT neither the spatial nor the time interval between points is saved - only the difference of their squares is saved:
ds 2 = c 2 dt 2 - dx 2 - dy 2 - dz 2 .
What is recorded here? This is a description of a special four-dimensional pseudo-Euclidean space - the so-called. Minkowski spaces - in which the distance between the points is equal to the difference of the squares of the differences of coordinates (and not the sum, as in ordinary Euclidean space).
From the point of view of the SRT, the movement of each body is a trajectory in the four-dimensional Minkowski space - the so-called. "World line".
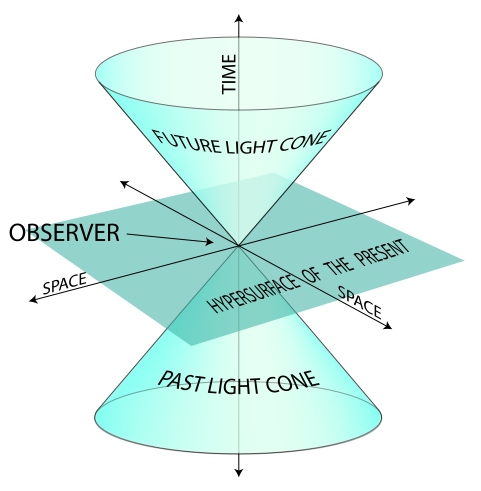
The cones in the figure are so-called. "Light cones" - the trajectories of objects moving at the speed of light.
Since now every object has its own time - and, moreover, it is free to change as you please - we, theoretically, can allow the “turns” of the world line, i.e. time travel.
(Traveling ahead in SRT is very easy - it is enough to move at a speed close to light - and this effect, albeit on a microscopic scale, has been successfully verified. Therefore, we are talking here and further about time travel in the sense of time travel back )
However, there are two big problems.
The first is that a material object can never reach the boundary of the light cone - it requires an infinite amount of energy.
The second is the curious features of the Lorentz transformations. Suppose we were able to move an object from point A to point B faster than the speed of light. Then there will necessarily be such a reference system in which the object first appears at point B, and then departs from point A. Simply put, movement is faster than light and there is movement in time in SRT, but only in a very non-trivial sense.
Indeed, how to understand this “there is such a system”? It turns out that for some observers there is a move into the past, but for a part - not. It depends solely on the speed of movement of the observer.
And, secondly, it turns out complete insanity with cause and effect. Obviously, the appearance of an object at point B is a consequence of its departure from point A. But for some observers, the effect occurs later than the cause. And for some - before. To this question we will return.
As a result, movement in a service station at a speed faster than light is prohibited. No, more precisely, not so: it is forbidden to transfer information between objects that are outside the light cone of each other. Otherwise, SRT faces intractable contradictions.
Movement initially faster than light is allowed - provided that systems moving faster than light do not exchange information. For example, the theory of inflation assumes that at the very beginning of the big bang, the family of newborn universes was moving away from each other at a speed many times higher than the light one. And there is no contradiction here - because Universes move farther apart from each other than light, light from one of them will never reach the other, and information will never be transmitted.
Let us return, however, to our sheep, i.e. to the discussion about the nature of time. Frankly, the service station has made quite a bit of understanding on this issue. What is the “internal time” of an object and how is it measured? Why is the temporal coordinate of Minkowski space so substantially opposed to spatial? Finally, what kind of a beast is such an “inertial reference system” and where can it be taken in reality?
He understood all these difficulties and Einstein, and therefore ten years later created the general theory of relativity (GTR), which finally confused everything.
So, for starters, all coordinates in GR (including the time) are simply the numbers of points on the axis. They have no more meaning, ask any.
Further, in these coordinates for each point of space-time it is necessary to determine the so-called. fundamental metric tensor g ab . What is this beast? This is a 4x4 matrix, which determines the distance between adjacent points. Suppose you are at a certain point (x 0 , x 1 , x 2 , x 3 ) and move in the direction (dx 0 , dx 1 , dx 2 , dx 3 ). Then you will go the distance:
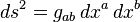
Hereinafter, over the indices repeating from above and below, summation is implied, i.e. in fact, the sum of 16 components is recorded here.
For an ordinary Euclidean space with an orthonormal basis, the matrix g is equal to unity. In the Minkowski space, g 00 = 1, g 11 = g 22 = g 33 = -1.
In the space of general relativity, the components of the metric tensor can be absolutely anything. Those. the distance between adjacent points is a (almost) arbitrary function of the coordinate difference. Well, the coordinates are completely arbitrary, remember?
If suddenly we want to move from one coordinate system to another, all tensors (including the fundamental metric one) will undergo such changes:

In general, it was the easy part :). In short, in GR, you can specify absolutely any coordinates and absolutely any point of reference, the only thing you have to do is calculate the fundamental metric tensor. The question about what “how to measure a unique time of an object” does not seem to be worth it - number the moments in time as your heart desires.
So, it seems that we have found out about space-time geometry, we now turn to objects in this space. From the distribution of the impulses and energies of the bodies we need to form a so-called. energy-momentum tensor T ab . It is exactly the same at its every point in space-time and sets the "density" of masses and energies.
Finally, we need derivatives of the fundamental tensor in all directions and derivatives (velocities) of all objects.
Now we can formulate how the geometry of space and the movement of bodies mutually influence each other.
The geometry of space changes as follows:
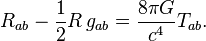
This equation is known as the Hilbert-Einstein equation. Here R ab is the so-called. Ricci tensor, expressed in terms of second partial derivatives of the fundamental metric tensor. (By the way, Gregory Perelman, in passing, proved the Poincaré theorem in his papers on just the Ricci tensor flows.)
What is written here? Knowing the energy-momentum tensor, metric tensor and derivatives of the metric tensor, we can calculate the second derivatives of the metric tensor. Thus, we determine how energy and momentum affect the geometry of space.
Now back. To determine how space geometry affects the movement of objects in it, we direct for each material point its distance ds 2 → min. Expanding this condition (for example, through the Lagrange principle), we obtain expressions for the second derivatives (“accelerations”) of objects. In particular, for massless particles (light), motion proceeds along a geodesic line expressed by the following equation:
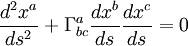
Here G a bc - the so-called. Christoffel symbols expressed in terms of the metric tensor.
There is a rather elegant analogy that describes the meaning of such a movement in understandable terms. Imagine that we pulled a sheet and at some points put heavy balls. In these places, the sheets bent and twisted - just as space is curved in the presence of energy and momentum.
Now we roll a light ball over our bed sheet. On level ground, it will move in a straight line; but, approaching massive points, it will bend its trajectory as if the heavy balls “pulled” it. This is the effect of attraction, actually caused by the curvature of the “space” in which the ball moves.
Ufff. Ok, let's summarize how objects move in terms of GR:
- we must know the current geometry of space (metric tensor) and the positions of energies and pulses in it (energy-momentum tensor);
- we also need to know the “speeds”, i.e. first partial derivatives of both;
- then we can calculate the second derivatives of both the metric tensor and world lines of objects, and, accordingly, make a modeling step.
Here, however, lies one very unpleasant moment. It is not very easy to ask about some initial state of the system: it may easily turn out that such a situation is simply unacceptable. There is no algorithm for constructing states; the sum of two admissible states may turn out to be an unacceptable state. There are exactly four exact analytical solutions to the Hilbert-Einstein equations: the Schwarzschild, Kerr, Reisner-Nordström and Kerr-Newman metrics, which describe a space with one material rotating / non-rotating charged / uncharged point.
Numerical solution of the equations is also hardly possible due to their tremendous complexity: for each point of the four-dimensional space, it is necessary to store four 16-digit matrices and solve 32 equations in each step, which is impossible with any acceptable accuracy at modern facilities.
Finished with a general theory, move on to more specific issues. Does UTO prohibit movement with time decreasing? Absolutely not. By aiming ds 2 → min, under some conditions we can get dt <0 for the optimal trajectory of motion. To try to formalize these “some conditions” is, to put it mildly, not easy; in particular, we can assume the existence of such a phenomenon as “wormholes” - special distortions of the geometry of space, allowing traveling (perhaps even safe for humans) at speeds faster than light (which is effectively a journey into the past - in a sense).
Has GRT clarified the nature of time? This is how to look. On the one hand, space, time, energy and momentum gained new meanings within the framework of the theory. On the other hand, questions to general relativity are somehow somehow not as simple and clear as to Newtonian mechanics. For example, all GR is covariant — written through tensors with subscripts (tensors with superscripts are called contravariant). Yes, I forgot to clarify - you can't just change the position of the index :), the expression changes from one coordinate system to another. So, why GRT is covariant - one of the big philosophical questions that is not something to answer - it is not very easy to realize. Because.
If you look at modern, more “advanced” theories - string ones - then they, in general, are about the same. They only operate not four-dimensional, but 10- or even 11-dimensional space (in which all but four dimensions are “collapsed” so that they have zero size for us). In this space, multidimensional surfaces are considered (branes — multidimensional membranes) along which string objects move. The object moves in such a way that its trajectory “sweeps” the minimum “area” on the surface of the brane. This is if to exaggerate. The meaning, in fact, is about the same, only the dimensions are larger.
Here you can also tell about the time in quantum mechanics - but dismiss it, it is already beyond my capabilities. There is almost nothing interesting in this place (quantum mechanics in this sense is more classical than GRT - its laws are explicitly written as time derivatives), except that the time coordinate of the object - like the spatial coordinate - obeys the uncertainty relation and cannot be determined in a pair with energy absolutely for sure.
Now it's time to return to the principle of causality. We see that GTR does not give any insight in this place. Causality does not exist. But you and I know perfectly well that it still exists, we very much see it in the world that is given to us in sensations.
GRT (and string theories) are all completely messed up. If Newtonian mechanics clearly did not allow any such travel in time, then GTR directly says: only the principle of causality hinders time travel, and nothing more. Mathematically, nothing forbids.
Hence, in order to get some scientific answer to this question, you will have to understand the meaning of the principle of causality. Alas, while in this place only the fog of war is observed.
There is one theory that comes precisely from causality as from the basis of the universe. This is the so-called. theory of causal dynamic triangulation, which builds a space of causal dependencies of events. (I again exaggerate, google / Yandex in more detail.) Alas, this theory is not particularly remarkable, it does not give any special insights - string theories still look more interesting. However, some physicists have a different opinion - see Lee Smolin, "Troubles with physics: the rise of string theory, the decline of science and what follows after this."
What is the result? In the end, I deceived all of you. I am very surprised if you have at least a little clearer how time works and whether traveling in it is possible; I myself was completely confused while writing this essay. I hope, on the other hand, that you now imagine the scale of the problem and realize that it is impossible to solve it with a swoop, having imagined any nonsense :).
If for you Wikipedia is the main stronghold of truth and knowledge, and the physical laws are unshakable - it’s time for you to work in the Inquisition. There are still so many people who disprove the theoretical inventions of 18th century physicists, not burned!
I have not seen such a level of militant ignorance for a long time, and it’s doubly strange to see him on Habré.
Since I, unlike the author, are a scientist , I will try in response to tell the inquisitive reader what we really know about the nature of time, causality, and time travel.
Time
')
In classical mechanics, time is considered absolute and unchanged in the sense that when moving from one reference system to another, the time intervals do not change:
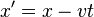



Here (x, y, z, t) are the coordinates in the old system, (x ', y', z ', t') are the coordinates in the new system. Hereinafter, it is assumed (to simplify the formulas) that one system moves relative to another parallel to the x axis with velocity v.
This is the so-called. Galilean transformations - what happens to the coordinates when changing the reference system. In the Galilean sense, the “flow of time” is one for the whole Universe, and the temporal coordinates of all objects are the same. In this case, classical mechanics does not interpret the uniqueness of the arrow of time; moreover, the very concept of the movement of time is not included in the Newton formulas in any way.
In classical mechanics, we ourselves introduce movement from the past to the future. Suppose we have a set of material points (coordinates and velocities) and acting forces. Next, we ask some interval dt and see how the system will evolve over time. No one prevents us from moving in the opposite direction and follow what happened to the system in the past.
However, “time travel” - i.e. the movement of one particular object on the scale t to the past - by Newtonian mechanics is forbidden (see above - the time flow is one for the whole Universe).
The situation became much more fun when Maxwell formulated his electrodynamics, and then Einstein, trying to solve the contradictions of electrodynamics and classical mechanics, created the theory of relativity.
In the framework of the special theory of relativity, in the transition from one inertial frame of reference to another, we already use such transformations:
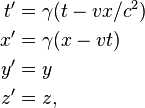 ,
,Where
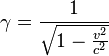 .
.Here, as is easy to see, each frame of reference has its own time scale. In the framework of the SRT neither the spatial nor the time interval between points is saved - only the difference of their squares is saved:
ds 2 = c 2 dt 2 - dx 2 - dy 2 - dz 2 .
What is recorded here? This is a description of a special four-dimensional pseudo-Euclidean space - the so-called. Minkowski spaces - in which the distance between the points is equal to the difference of the squares of the differences of coordinates (and not the sum, as in ordinary Euclidean space).
From the point of view of the SRT, the movement of each body is a trajectory in the four-dimensional Minkowski space - the so-called. "World line".

The cones in the figure are so-called. "Light cones" - the trajectories of objects moving at the speed of light.
Since now every object has its own time - and, moreover, it is free to change as you please - we, theoretically, can allow the “turns” of the world line, i.e. time travel.
(Traveling ahead in SRT is very easy - it is enough to move at a speed close to light - and this effect, albeit on a microscopic scale, has been successfully verified. Therefore, we are talking here and further about time travel in the sense of time travel back )
However, there are two big problems.
The first is that a material object can never reach the boundary of the light cone - it requires an infinite amount of energy.
The second is the curious features of the Lorentz transformations. Suppose we were able to move an object from point A to point B faster than the speed of light. Then there will necessarily be such a reference system in which the object first appears at point B, and then departs from point A. Simply put, movement is faster than light and there is movement in time in SRT, but only in a very non-trivial sense.
Indeed, how to understand this “there is such a system”? It turns out that for some observers there is a move into the past, but for a part - not. It depends solely on the speed of movement of the observer.
And, secondly, it turns out complete insanity with cause and effect. Obviously, the appearance of an object at point B is a consequence of its departure from point A. But for some observers, the effect occurs later than the cause. And for some - before. To this question we will return.
As a result, movement in a service station at a speed faster than light is prohibited. No, more precisely, not so: it is forbidden to transfer information between objects that are outside the light cone of each other. Otherwise, SRT faces intractable contradictions.
Movement initially faster than light is allowed - provided that systems moving faster than light do not exchange information. For example, the theory of inflation assumes that at the very beginning of the big bang, the family of newborn universes was moving away from each other at a speed many times higher than the light one. And there is no contradiction here - because Universes move farther apart from each other than light, light from one of them will never reach the other, and information will never be transmitted.
Let us return, however, to our sheep, i.e. to the discussion about the nature of time. Frankly, the service station has made quite a bit of understanding on this issue. What is the “internal time” of an object and how is it measured? Why is the temporal coordinate of Minkowski space so substantially opposed to spatial? Finally, what kind of a beast is such an “inertial reference system” and where can it be taken in reality?
He understood all these difficulties and Einstein, and therefore ten years later created the general theory of relativity (GTR), which finally confused everything.
So, for starters, all coordinates in GR (including the time) are simply the numbers of points on the axis. They have no more meaning, ask any.
Further, in these coordinates for each point of space-time it is necessary to determine the so-called. fundamental metric tensor g ab . What is this beast? This is a 4x4 matrix, which determines the distance between adjacent points. Suppose you are at a certain point (x 0 , x 1 , x 2 , x 3 ) and move in the direction (dx 0 , dx 1 , dx 2 , dx 3 ). Then you will go the distance:
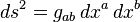
Hereinafter, over the indices repeating from above and below, summation is implied, i.e. in fact, the sum of 16 components is recorded here.
For an ordinary Euclidean space with an orthonormal basis, the matrix g is equal to unity. In the Minkowski space, g 00 = 1, g 11 = g 22 = g 33 = -1.
In the space of general relativity, the components of the metric tensor can be absolutely anything. Those. the distance between adjacent points is a (almost) arbitrary function of the coordinate difference. Well, the coordinates are completely arbitrary, remember?
If suddenly we want to move from one coordinate system to another, all tensors (including the fundamental metric one) will undergo such changes:

In general, it was the easy part :). In short, in GR, you can specify absolutely any coordinates and absolutely any point of reference, the only thing you have to do is calculate the fundamental metric tensor. The question about what “how to measure a unique time of an object” does not seem to be worth it - number the moments in time as your heart desires.
So, it seems that we have found out about space-time geometry, we now turn to objects in this space. From the distribution of the impulses and energies of the bodies we need to form a so-called. energy-momentum tensor T ab . It is exactly the same at its every point in space-time and sets the "density" of masses and energies.
Finally, we need derivatives of the fundamental tensor in all directions and derivatives (velocities) of all objects.
Now we can formulate how the geometry of space and the movement of bodies mutually influence each other.
The geometry of space changes as follows:
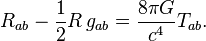
This equation is known as the Hilbert-Einstein equation. Here R ab is the so-called. Ricci tensor, expressed in terms of second partial derivatives of the fundamental metric tensor. (By the way, Gregory Perelman, in passing, proved the Poincaré theorem in his papers on just the Ricci tensor flows.)
What is written here? Knowing the energy-momentum tensor, metric tensor and derivatives of the metric tensor, we can calculate the second derivatives of the metric tensor. Thus, we determine how energy and momentum affect the geometry of space.
Now back. To determine how space geometry affects the movement of objects in it, we direct for each material point its distance ds 2 → min. Expanding this condition (for example, through the Lagrange principle), we obtain expressions for the second derivatives (“accelerations”) of objects. In particular, for massless particles (light), motion proceeds along a geodesic line expressed by the following equation:
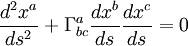
Here G a bc - the so-called. Christoffel symbols expressed in terms of the metric tensor.
There is a rather elegant analogy that describes the meaning of such a movement in understandable terms. Imagine that we pulled a sheet and at some points put heavy balls. In these places, the sheets bent and twisted - just as space is curved in the presence of energy and momentum.
Now we roll a light ball over our bed sheet. On level ground, it will move in a straight line; but, approaching massive points, it will bend its trajectory as if the heavy balls “pulled” it. This is the effect of attraction, actually caused by the curvature of the “space” in which the ball moves.
Ufff. Ok, let's summarize how objects move in terms of GR:
- we must know the current geometry of space (metric tensor) and the positions of energies and pulses in it (energy-momentum tensor);
- we also need to know the “speeds”, i.e. first partial derivatives of both;
- then we can calculate the second derivatives of both the metric tensor and world lines of objects, and, accordingly, make a modeling step.
Here, however, lies one very unpleasant moment. It is not very easy to ask about some initial state of the system: it may easily turn out that such a situation is simply unacceptable. There is no algorithm for constructing states; the sum of two admissible states may turn out to be an unacceptable state. There are exactly four exact analytical solutions to the Hilbert-Einstein equations: the Schwarzschild, Kerr, Reisner-Nordström and Kerr-Newman metrics, which describe a space with one material rotating / non-rotating charged / uncharged point.
Numerical solution of the equations is also hardly possible due to their tremendous complexity: for each point of the four-dimensional space, it is necessary to store four 16-digit matrices and solve 32 equations in each step, which is impossible with any acceptable accuracy at modern facilities.
Finished with a general theory, move on to more specific issues. Does UTO prohibit movement with time decreasing? Absolutely not. By aiming ds 2 → min, under some conditions we can get dt <0 for the optimal trajectory of motion. To try to formalize these “some conditions” is, to put it mildly, not easy; in particular, we can assume the existence of such a phenomenon as “wormholes” - special distortions of the geometry of space, allowing traveling (perhaps even safe for humans) at speeds faster than light (which is effectively a journey into the past - in a sense).
Has GRT clarified the nature of time? This is how to look. On the one hand, space, time, energy and momentum gained new meanings within the framework of the theory. On the other hand, questions to general relativity are somehow somehow not as simple and clear as to Newtonian mechanics. For example, all GR is covariant — written through tensors with subscripts (tensors with superscripts are called contravariant). Yes, I forgot to clarify - you can't just change the position of the index :), the expression changes from one coordinate system to another. So, why GRT is covariant - one of the big philosophical questions that is not something to answer - it is not very easy to realize. Because.
If you look at modern, more “advanced” theories - string ones - then they, in general, are about the same. They only operate not four-dimensional, but 10- or even 11-dimensional space (in which all but four dimensions are “collapsed” so that they have zero size for us). In this space, multidimensional surfaces are considered (branes — multidimensional membranes) along which string objects move. The object moves in such a way that its trajectory “sweeps” the minimum “area” on the surface of the brane. This is if to exaggerate. The meaning, in fact, is about the same, only the dimensions are larger.
Here you can also tell about the time in quantum mechanics - but dismiss it, it is already beyond my capabilities. There is almost nothing interesting in this place (quantum mechanics in this sense is more classical than GRT - its laws are explicitly written as time derivatives), except that the time coordinate of the object - like the spatial coordinate - obeys the uncertainty relation and cannot be determined in a pair with energy absolutely for sure.
Now it's time to return to the principle of causality. We see that GTR does not give any insight in this place. Causality does not exist. But you and I know perfectly well that it still exists, we very much see it in the world that is given to us in sensations.
GRT (and string theories) are all completely messed up. If Newtonian mechanics clearly did not allow any such travel in time, then GTR directly says: only the principle of causality hinders time travel, and nothing more. Mathematically, nothing forbids.
Hence, in order to get some scientific answer to this question, you will have to understand the meaning of the principle of causality. Alas, while in this place only the fog of war is observed.
There is one theory that comes precisely from causality as from the basis of the universe. This is the so-called. theory of causal dynamic triangulation, which builds a space of causal dependencies of events. (I again exaggerate, google / Yandex in more detail.) Alas, this theory is not particularly remarkable, it does not give any special insights - string theories still look more interesting. However, some physicists have a different opinion - see Lee Smolin, "Troubles with physics: the rise of string theory, the decline of science and what follows after this."
What is the result? In the end, I deceived all of you. I am very surprised if you have at least a little clearer how time works and whether traveling in it is possible; I myself was completely confused while writing this essay. I hope, on the other hand, that you now imagine the scale of the problem and realize that it is impossible to solve it with a swoop, having imagined any nonsense :).
Source: https://habr.com/ru/post/174123/
All Articles