Computer Poker Abstractions

Computer poker is a very nontrivial task, primarily because of the huge number of game states, which is so great that you don’t have to dream of solving this game directly. The only way to somehow teach the machine to play poker is to switch to abstraction - a reduced copy of poker, in which situations of the original game, which are similar in a strategic sense, are combined together. This article is devoted to issues of abstractions in poker.

This publication is to some extent referred to the first part and assumes that the reader is familiar with the rules of poker. I will try to adhere to the popular style of presentation, and for those interested in the details there are links to literature and discussion in the comments.

Why do we need abstraction?

In order to imbued with the scale of the problem of computer poker, I recommend to get acquainted with the report [1], where the dimensions of both limit and no limit poker disciplines are given. Even for the most “simple” Limit Texas Hold'em, there are exactly 319,365,922,522,608 game states in which you need to make a decision. At the same time, in this type of poker, there are only 6378 different non-terminal betting patterns and all the wealth of game states due to card combinations. For no-limit and pot-limit disciplines, the possibilities to bet on dozens of orders of magnitude more than for their limit counterpart - in no-limit hold'em with a stack of 500 blinds of the order of ~ 10 ⁶¹ non-terminal stories. After reading the above, the reader should begin to doubt the ability of modern computing to solve poker in its immediate presentation.
')
Methods of simplifying the original game come to the rescue, which merge the strategically close states of this game into indistinguishable states of a new game called abstraction . For poker, we can distinguish two classes of problems solved by the transition to abstraction:

• The problem of bets in unlimited and pot-limit games.
• The problem of representing the hands of players .

Bets and their presentation in an abstract game

The problem of bets is particularly relevant in pot-limit and no-limit poker disciplines, although it is sometimes necessary to reduce the number of betting patterns in limit games with a large number of players. One of the most popular methods here is the discretization of rates, when the ranges of rates are divided into intervals and all manipulations are further carried out with the rates attached to the ranges.

Consider the discretization option for unlimited poker, where the stakes are determined as follows: h - half of the bank, p - bet to the bank, d - double the bank, a - all-in. All other rates will be correlated to the closest of the above. At first glance, such an abstraction of bets is quite adequate and, indeed, the bots using it demonstrate a good level of playing with opponents who adhere to the same betting scheme (see, for example, [2]). But if the enemy suddenly makes an arbitrary bet, which is very different from the discrete one, then the inappropriate behavior of the bot is provided to us. The most obvious potential vulnerability is the opponent’s committing the minimum allowable bet, after which the bot can simply fold. In addition, bets on the boundaries between discrete ranges lead to the adoption by the bot of “overvalued” or “undervalued” decisions, which is fraught with losing money at a distance and disclosing the bot by man. Adding more discrete ranges does not save the situation, as the number of abstract game states increases and you have to reduce the quality of the abstract representation of maps.

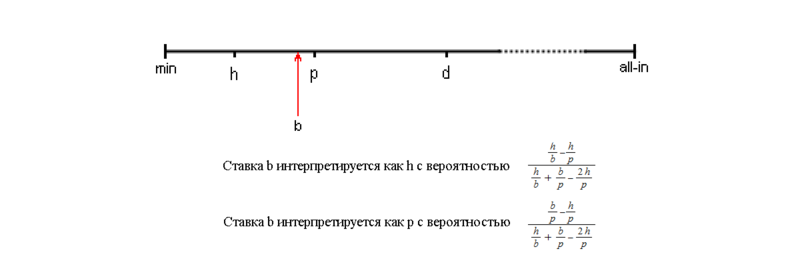
Discretization of the real bet b to the abstract bet p in the case of a “hard” broadcast or to one of the abstract rates h and p in the “soft” one.

The above scheme for transferring the stakes of a real game into an abstract one is called “hard”. There is another, “soft” way of transmitting bets, the essence of which is that the correlation of a real bet to one or another abstract is determined randomly, and the closer the real bet to the abstract, the higher the likelihood of correlation. In the presentation [3] there is information that the “soft” way of broadcasting allows the bot to be less exploited by bet sizes, but at the same time less profitable.

When building a poker agent that is focused on the game with people, the bets are often discretized by analyzing real hand games, after which each game state is assigned its own bets discretization scheme. Nevertheless, this approach is still vulnerable after the identification of the scheme for constructing an abstraction. Discretization is not the only way to represent poker bets. It is also possible that the poker agent seeks to supplement the bank with a strictly defined amount in order to bring the bank into conformity with the value laid down in the abstraction. Obviously, such a trick immediately exposes the bot and is not without serious flaws, for example, a minor excess of the pledged bank size can force the bot to discard cards.

Recently, a method has been developed to build poker betting abstractions, which introduces another gaming agent who decides what bet to make in a particular game situation. In [4-5], instead of all possible bets in each game state, players are allowed to make only three: the minimum bet (L), the maximum bet (H) or go to all-in. In this case, the decision on which of the two bets L or H needs to be made is taken by the new gaming agent. The obvious advantage of this approach is the complexity of the operation of the bot size rates, but this raises issues related to the training of the newly introduced agent, finding specific values ​​for the L and H rates, organizing the presentation of abstraction as a whole.


Different ways of presenting bets in no-limit poker.


Sometimes there are abstractions in which the number of bets on trading circles is limited or the history of previous circles is completely absent. But today, such approaches are not particularly popular, since they give rise to weak poker agents.

Card combinations in abstractions

The most difficult and most important thing when building an abstraction for poker is the presentation of card combinations. That is what determines how adequately the bot will perceive the current game situation and make strategically correct decisions.

Below is a table from the report [1], which lists the sizes of the sets of various combinations of cards in Texas Hold'em for each round of betting. The first column presents the variants of the distribution of pocket cards to both players in combination with the community cards on the board. The second column contains the same information, but for one player, i.e. for combinations of one pair of pocket cards and community cards. And, finally, the last column contains the number of nonequivalent classes of card combinations for one player. Recall that the equivalent combinations are such sets of card combinations, in which you can get any other combination from the same set by replacing suits. It is obvious that equivalent combinations contain the same strategic information.

Circle of trade	Total for two players	Total for one player	Nonequivalent for one player
Preflop	1,624,350	1,326	169
The flop	28,094,757,600	25,989,600	1,286,792
Turn	1,264,264,092,000	1,221,511,200	55,190,538
River	55,627,620,048,000	56,189,515,200	2,428,287,420

An example of an equivalent class is the combination AKx|TxJy82x on the third round of betting, where AKx are player's pocket cards, TxJy82x are cards on the board in the order of their appearance, and x and y ( x!=y , of course) can take one of four values ​​of suits {c,s,h,d} . Thus, the class AKx|TxJy82x contains 12 absolutely identical combinations {AKc|TcJs82c, AKs|TsJc82s, ...} . We agree to call the combination, recorded in the form of AKx|TxJy82x , the player's hand , although this is somewhat at odds with the generally accepted definition . Nevertheless, the term hand is perfectly suited to the definition of private information about cards, fully accessible only to one player.

Even after bringing the hands to equivalent classes there are too many of them for direct consideration, it is therefore necessary to resort to grouping these equivalent classes into new, abstract classes. Of course, now this procedure will occur with some loss of information about the original equivalent classes.

For an example of such a grouping of hands, consider preflop, since there are only 169 non-equivalent pocket pairs on it. Many interested readers are familiar with the name of a famous theorist and poker player David Sklansky, one of whose achievements is a detailed preflop strategy. The figure below shows the grouping of starting hands by their strategic value, proposed by Sklansky [6]. This division into eight classes is not the only true, but gives a good idea of ​​the principles of constructing card abstractions in poker.



Unfortunately, starting from the flop, manual analysis of card combinations is very tedious and ungrateful, so you have to resort to other methods of analyzing and splitting hands into classes. It will be a question of numerical characteristics of card combinations, which allow grouping card combinations according to selected properties.

One of the very first characteristics used was the rank of the hand (Hand Strength, HS ), which is defined as the proportion of all possible ready-made combinations for the opponent, inferior in strength to the ready-made combination for the player. For example, HS(AKx|TxJy82x)=1.0 since there is a ready-made senior flash, but HS(AxKy|TzJx82z)~0.43 , which is not surprising, since any pair of cards with the z-suit from your opponent gives him an advantage.

The first thing that strikes the analysis of HS is that this indicator says nothing about how the player’s hand behaves in subsequent trading circles, not to mention that the distribution history does not affect the value of this indicator in any way. In order to fill in the missing information, starting with the flop, two more indicators PPot (Positive Potential) and NPot (Negative Potential) are introduced. The first of these PPot indicators represents the likelihood that a player’s current hand will improve after a new card appears on the table. Improvement means that your opponent will not have new ready-made combinations that will be older than the player's ready-made combination. Similarly, Npot is the probability that a player’s hand will deteriorate with a new card on the table. A detailed description of these indicators and their calculation procedures can be found in [7-8]. For the above example, PPot(AKx|TxJy82x)=0 and NPot(AKx|TxJy82x)~0 , which is not surprising, since the opponent has to rely only on a full house if he has ready two pairs. For the second case, PPot(AxKy|TzJx82z)~0.15 and NPot(AxKy|TzJx82z)~0.22 and we see that NPot quite high due to the fact that the opponent can get the missing card with the x-suit to assemble the flash.

In [9], information is given that the square of the expected rank of the hand E[HS ² ] allows to obtain a higher-quality abstraction, since this indicator gives more advantages to the player’s strong hands and differentiates them from the hands that have a high potential ( PPot ). It is logical, because hands with the same rank, but with different potential, should be played strategically in different ways.

Three indicators {HS, PPot, NPot} make it possible to more accurately characterize a player’s hand, but their simultaneous consideration may be somewhat inconvenient, the poet often resort to calculating the effective hand strength ( EHS ), which is given by one of two formulas [7 -8]: EHS ₁ = HS×(1−NPot)+(1−HS)×PPot , or, EHS ₂ = HS+(1−HS)×PPot . The difference between the two formulas is that EHS ₂ gives a more “optimistic” prediction, which is sometimes necessary for working through a more aggressive game.

Another indicator that many have already guessed is the chance of winning the hand or the expected rank of the hand at the showdown (expected hand strength, E[HS] ). As is clear from the name of this feature, it represents the proportion of cases where the current player will get a combination older than the opponent’s possible combination after playing the game before the showdown. The advantage of this indicator lies in the fact that it already includes information on the dynamics of the hand in all subsequent trading circles up to the opening, unlike NPot and PPot , predicting only one street ahead. In the examples above, against the opponent's random hand, these figures have the following values: E[HS](AKx|TxJy82x)~0.99 and E[HS](AxKy|TzJx82z)~0.42 .

All of the above indicators have a number of common shortcomings. The first one, the most noticeable for experienced poker players, is that these figures are calculated on the assumption that any hand is in the opponent’s hands. The point is that in poker, a very small percentage of hands comes to the showdown, which means that when calculating HS , PPot , NPot or E[HS] we put our opponent all possible pocket cards that he may never have. This in turn makes the estimates of such indicators unpredictably overestimated. In order to somehow correct this deficiency, we often use hand weighting , which is possible for the opponent, depending on the game situation. In particular, such a weighting can be carried out using opponent modeling .

The second drawback lies in the fact that the use of these indicators still leads to the loss of information about the player’s hand, although this is not so obvious. First of all, it concerns the “memory” of the hand, namely the information about the sequence in which the cards appeared on the board. For example, it is obvious that HS(AKx|QJT5x)=HS(AKx|JT5Qx) , where in the first case the player on the flop already had a straight-flush combination, and in the second - no. Moreover, often hands that require different strategic decisions have similar numerical values, which can lead (and lead) to mistakes in learning the poker machine to play.

Further manipulations with numerical indicators in order to build abstractions are reduced to grouping various categories of hands into classes according to certain values ​​of these indicators. For example, if we want to have a total of five classes on each trading cycle, then we can group all hands by the following values E[HS] :
[0.0–0.2] [0.2–0.4] [0.4–0.6] [0.6–0.8] [0.8–1.0] .
Now the abstract poker game will manipulate five classes of hands, rather than the original card combinations. In order for such an abstract game to be complete, it is also necessary to calculate the transition probabilities between classes at the change of rounds of trading and set a payout matrix that lists the “profitability” of one abstract hand class relative to another.

Abstraction with the help of grouping hands into classes can be performed both manually and using automated procedures, for example, using data clustering methods. Manual creation of abstractions allows in some measure to provide an understanding of bot solutions, to facilitate debugging and adjustment of the strategy, but it is a very laborious process. Automatic grouping methods are often guided by criteria that are not always suitable for poker tasks. On the other hand, the automatic approach allows you to easily and quickly manipulate the parameters of abstractions, which allows you to quickly and optimally select the appropriate configuration.

The above example of hand-splitting into classes using five predefined intervals of values E[HS] has one drawback - hands are distributed unevenly into classes — only a couple of hands fall into some range of values E[HS] , and the rest will be overpopulated. To remedy this situation, use different techniques, from manually editing classes, calculating quantiles, splitting into nested classes, k-means and others.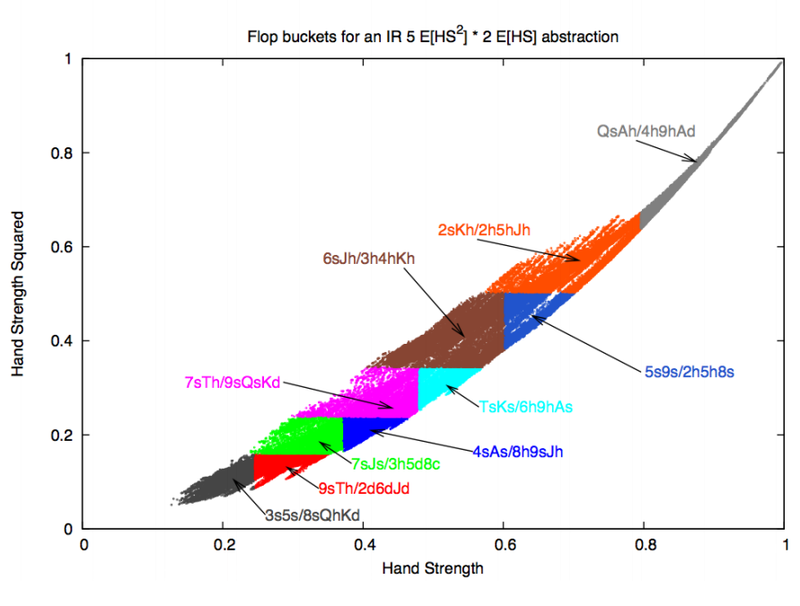


An example of grouping hands using the E[HS ² ] and E[HS] indicators on the flop, divided into nested classes.

Conclusion

In my humble opinion, modern computer poker is a game of abstractions in which that agent wins, whose abstraction turned out to be better, more accurate, and, not least, less. The size of the abstraction is mentioned not in vain, because it depends on him the time spent learning the agent to play. And whether it will be millennia, years, or a couple of hours - depends on the researcher who designs the structure of abstraction. Unfortunately, this publication can in no way pretend to a complete review of various approaches to the construction of abstractions, since there are a lot of them. Nevertheless, I think that the main points in this area are reflected and the goal to get the reader interested in the problems of computer poker has been achieved.