Sudoku solution methods

1. Basics

Most of us habrazhiteli know what sudoku . I will not talk about the rules, but immediately move on to the methods.
To solve a puzzle, no matter how complicated or simple, the cells are initially searched for obvious to fill.

1.1 "The Last Hero"

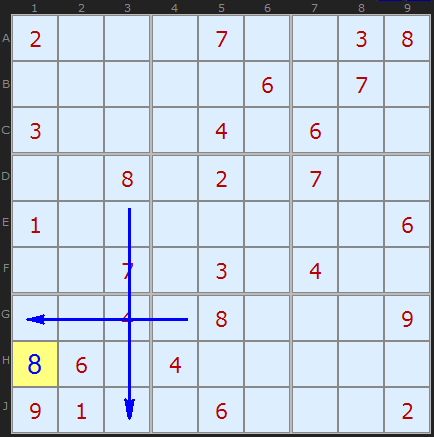
Consider the seventh square. Only four free cells mean something can be quickly filled.
" 8 " on D3 blocks the filling of H3 and J3 ; likewise " 8 " on G5 closes G1 and G2
With a clear conscience, we put " 8 " on H1

1.2 “Last Hero” in the row

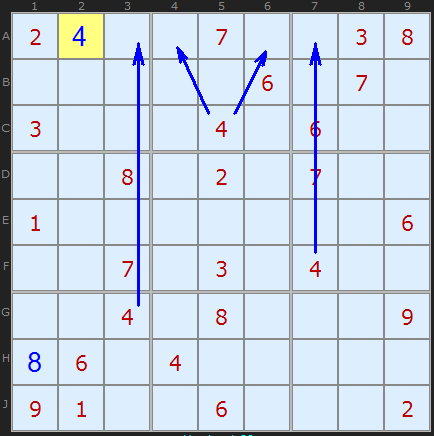
After viewing the squares on the obvious solutions, go to the columns and rows.
Consider " 4 " on the field. It is clear that it will be somewhere in row A.
We have " 4 " on G3 , which is A3 , there is " 4 " on F7 , which removes A7 . And another " 4 " in the second square prohibits its repetition on A4 and A6 .
"Last Hero" for our " 4 " is A2

1.3 “No choice”

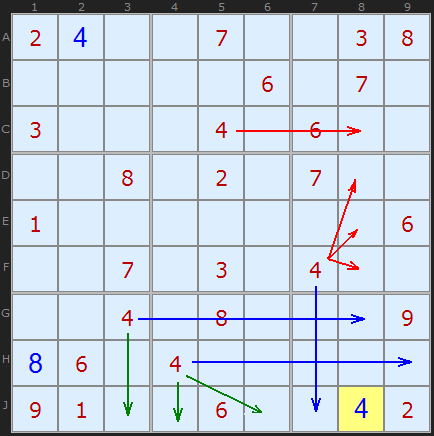
Sometimes there are several reasons for a particular location. " 4 " in J8 would be a great example.
The blue arrows indicate that this is the last possible number in the square. The red and blue arrows give us the last number in column 8 . The green arrows give the last possible number in row j .
As we see, we have no choice, except for how to put this " 4 " in place.

1.4 "And who, if not me?"

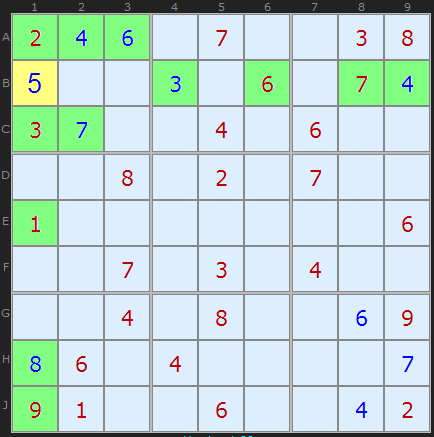
Filling numbers is easier to carry out the above methods. However, checking the number as the last possible value also gives results. The method should be used when it seems that all the numbers are, but something is missing.
" 5 " in B1 is set on the assumption that all numbers from " 1 " to " 9 ", except for " 5 ", are in the row, column and square (marked in green).
')
In the jargon is the “ Naked Loner ”. If the field is filled with possible values ​​(candidates), then in the cell such a number will be the only possible one. Developing this technique, you can search for “ Hidden loners ” - numbers that are unique to a particular row, column, or square.

2. "Naked mile"

2.1 "Naked" couples

" " Naked "pair " - a set of two candidates located in two cells belonging to one common block: row, column, square.
It is clear that the correct solutions of the puzzle will be only in these cells and only with these values, while all other candidates from the general block can be removed.

In this example, several "bare pairs".
Red in row A highlights cells A2 and A3 , both containing " 1 " and " 6 ". I don’t know exactly how they are located here, but I can calmly remove all the other " 1 " and " 6 " from row A (marked in yellow). Also, A2 and A3 belong to the common square, so remove " 1 " from C1 .

2.2 "Threesome"

“Naked triples” is a complicated version of “naked pairs”.
Any group of three cells in one block containing a total of three candidates is a “bare three” . When such a group is found, these three candidates can be removed from other cells of the block.

Combinations of candidates for the "bare three" can be:

[abc] [abc] [abc] // three numbers in three cells.
[abc] [abc] [ab] // any combination.
[abc] [ab] [ab] // any combination.
[ab] [ac] [bc]

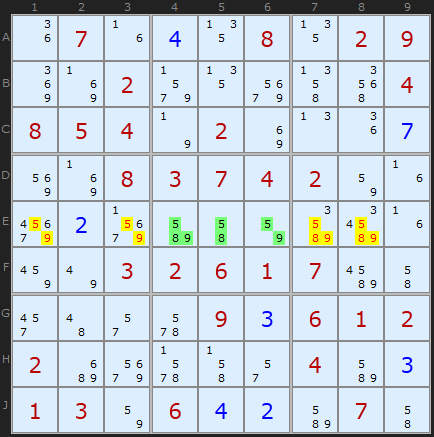
In this example, everything is pretty obvious. In the fifth square, cells E4 , E5 , E6 contain [ 5,8,9 ], [ 5,8 ], [ 5,9 ], respectively. It turns out that in general these three cells have [ 5, 8, 9 ], and only these numbers can be there. This allows us to remove them from other candidates of the block. This trick gives us the solution " 3 " for cell E7 .

2.3 “The Magnificent Four”

"The" naked "four" is a very rare phenomenon, especially in its full form, and yet gives results when detected. The logic of the solution is the same as that of the “bare triples” .


In this example, in the first square, cells A1 , B1 , B2, and C1 generally contain [ 1,5,6,8 ], therefore these numbers will occupy only these cells and no others. We remove the highlighted yellow candidates.

3. "All secret becomes clear"

3.1 Hidden pairs

A great way to uncover a field is to search for hidden pairs . This method allows you to remove unnecessary candidates from the cell and give development to more interesting strategies.

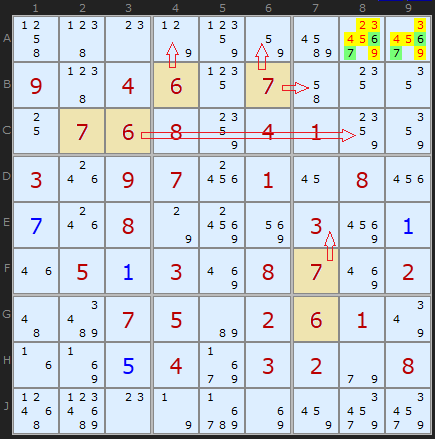
In this puzzle we see that 6 and 7 are in the first and second squares. In addition, 6 and 7 are in column 7 . Combining these conditions, we can assert that in cells A8 and A9 there will be only these values ​​and we remove all other candidates.


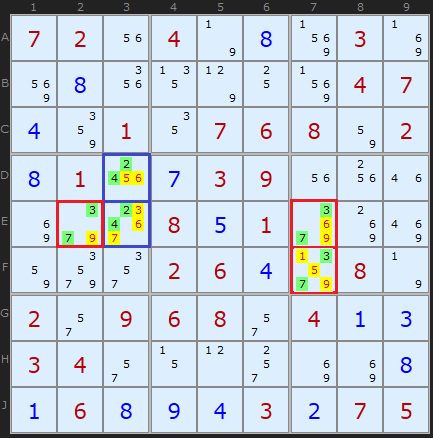
A more interesting and challenging example of hidden pairs . The pair [ 2,4 ] in D3 and E3 , which removes 3 , 5 , 6 , 7 of these cells, is highlighted in blue. Red highlighted two hidden pairs consisting of [ 3,7 ]. On the one hand, they are unique for two cells in column 7 , on the other hand, for row E. Yellow highlighted candidates are removed.

3.1 Hidden threes

We can develop hidden pairs to hidden triples or even hidden fours . The hidden triple consists of three pairs of numbers located in one block. Such as [a, b, c], [a, b, c] and [a, b, c]. However, as in the case of "bare threes" , in each of the three cells do not necessarily have to be three numbers. Only three numbers in three cells will work. For example, [ab], [ac], [bc]. Hidden triples will be masked by other candidates in the cells, so you first need to make sure that the triple is applicable to a particular block.


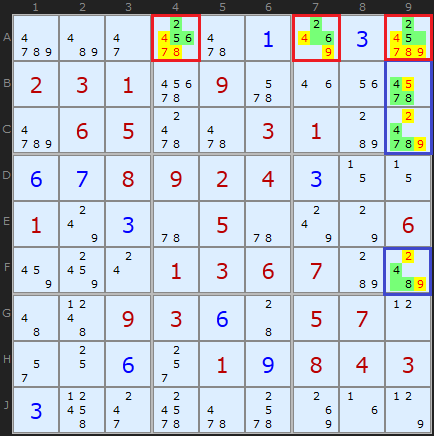
In this complex example, there are two hidden triples . The first, marked in red, in column A. Cell A4 contains [ 2,5,6 ], A7 - [ 2,6 ] and cell A9 - [ 2,5 ]. These three cells are the only ones where there can be 2, 5 or 6, therefore only they will be there. Therefore remove the extra candidates.

The second, in column 9 . [ 4,7,8 ] unique to cells B9 , C9 and F9 . Using the same logic, we remove the candidates.

3.1 Hidden Fours

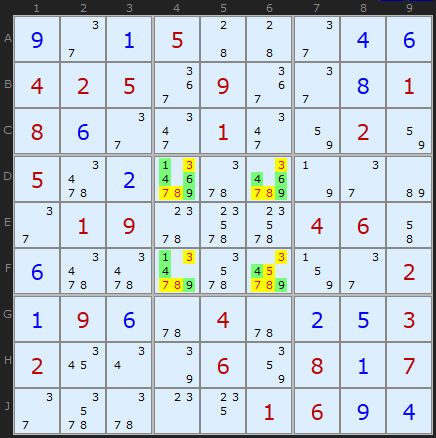
A wonderful example of hidden fours . [ 1,4,6,9 ] in the fifth square can be only in four cells D4 , D6 , F4 , F6 . Following our logic, we remove all other candidates (marked in yellow).

4. "Non-Resin"

If any of the numbers appears twice or three times in one block (row, column, square), then we can remove this number from the conjugate block. There are four types of pairing:

1. Pair or Troika in the square - if they are located in one line, then you can remove all other values ​​from the corresponding line.
2. Pair or Troika in a square - if they are located in one column, then you can remove all other values ​​from the corresponding column.
3. Pair or Troika in a row - if they are located in one square, then you can remove all other values ​​from the corresponding square.
4. Pair or Troika in the column - if they are located in the same square, then you can remove all other similar values ​​from the corresponding square.

4.1 Pointing pairs, triples

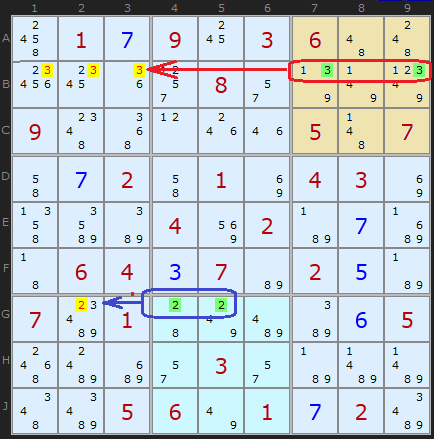
As an example, I will show this puzzle. In the third square, " 3 " is found only in B7 and B9 . Following statement # 1 , we remove candidates from B1 , B2 , B3 . Similarly, “ 2 ” from the eighth square removes the possible value from G2 .


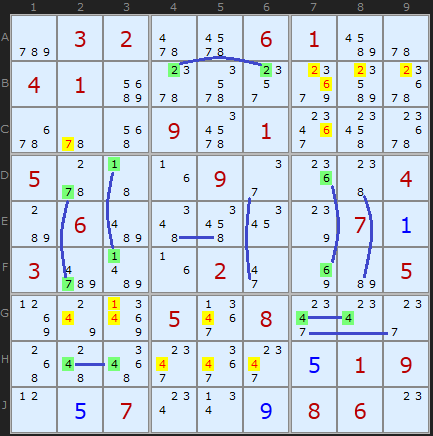
Special puzzle. Very difficult to solve, but if you look closely, you can see a few pointing pairs . It is clear that it is not always necessary to find them all in order to advance in the solution, but each such finding makes it easier for us.

4.2 Reduce unabsorbable

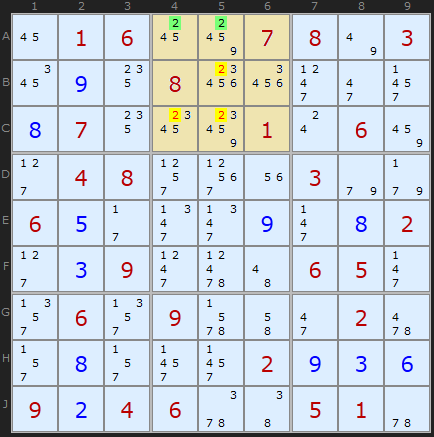
This strategy includes accurate analysis and comparison of rows and columns with the contents of the squares (rules № 3 , № 4 ).
Consider line A. " 2 " are possible only in A4 and A5 . Following the rule number 3 , remove the " 2 " of their B5 , C4 , C5 .


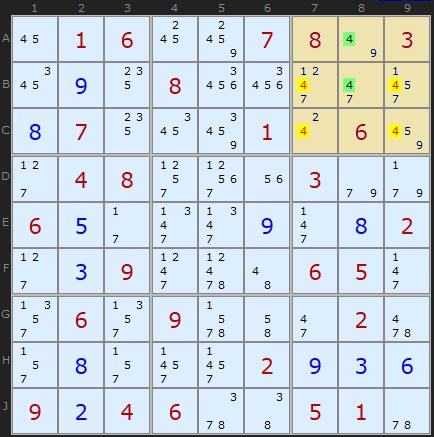
Continue to solve the puzzle. We have the only arrangement " 4 " within one square in the 8th column. According to rule number 4 , we remove unnecessary candidates and, in addition, we obtain solution “ 2 ” for C7 .

Afterword

There are hundreds of algorithms and programs for solving Sudoku. Sometimes it’s enough to hover the webcam to get the result. However, for brain training and scrolling algorithms in your head, it will be useful to sit with a pen and paper solving a sudoku.
The article cited the basic solution algorithms. Yes, yes, it is basic. The next step is to analyze advanced and complex techniques. Thanks for attention.