Quantum mechanics for all, for nothing, and let no one leave offended: part two
Hello! Quantum mechanics continues in the second part of Eliezer Yudkowski’s cycle, and today you will learn a little more about configurations, and also understand why the observation process affects the object of observation. Critics of dull humanity, of course, will also abound. In general, do not pass by!
← read the first part
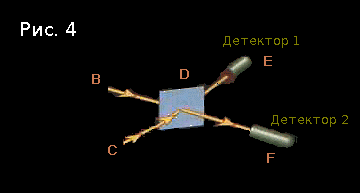
One of the key points in quantum mechanics is that configurations always describe the state of more than one particle. Look: this time we will slightly complicate the experiment from the first article, at the same time sending two photons to D - from points B and C.
')
The initial configuration is “the photon flies from B to D , and the photon flies from C to D ”. Like last time, we will assume that its amplitude is equal to (-1 + 0 i ).
In D there is a semi-silvered mirror already familiar to us, which multiplies the amplitude by 1 when a photon is reflected, and by - i - when a photon passes ( i was in the original, but this is not quite true - approx. Lane ).
Consider four cases:
Please note that completely different situations in the first and fourth cases led to the same resulting configuration! Therefore, when we consider the final configuration value “photon flies to E , and photon flies to F ”, we will get (1 + 0 i ) + (−1 + 0 i ) = 0. And this means that this will never happen . Both detectors cannot work at the same time.
One important lesson to be learned from this experiment: photons are indistinguishable . If there were even the smallest difference between the two photons, the result of the experiment would be completely different.
In the classical model of the world, where amplitudes can be considered as probabilities, everyone is free to choose the way of grouping outcomes. Let me explain: I could consider all four outcomes described above as different; could distinguish only two outcomes (“each detector arrives in a photon” and “both photons arrive in one detector”); could do something else. And nothing would have changed. Similarly, if I need to calculate the probability that odd numbers fall out on two dice, I can compose a sign of 36 possible throw results — and I can immediately divide the faces into even and odd numbers and reduce the number of outcomes to four.
Why doesn't this work in a quantum model? Because the probabilities of events nonlinearly depend on amplitudes, and the sum square, as is known, cannot be replaced by the sum of squares:
From this it follows that we can experimentally establish which configurations are different and which ones are not. In particular, these configurations are identical:
And here is the second important lesson (which I hinted in the first paragraph, and which I will talk about in detail later): the laws of quantum mechanics are not applicable to individual particles . The strategy "divide and conquer" does not work here. This is a great temptation - without much difficulty to consider the behavior of each elementary particle, and then in some way put together a coherent picture of the world from pieces of a mosaic ... But it is this approach that for so many years inhibited the development of quantum mechanics.
Immediately take the bull by the horns. When are the two configurations different?
To answer this question, we will conduct the following experiment:

At point S is the sensor. The only thing he does is transfer to another state when a photon passes through it. We assume that at the beginning of the experiment, the sensor is in the
So, the initial configuration:
What happens after the photon arrives at A ? In the previous version of this experiment - without a sensor - the possible configurations were “photon flying from A to B ” with amplitude i and “photon flying from A to C ” with amplitude −1. But since each configuration describes the complete state of the system, we must include the state of the sensor in their descriptions. So:
Now mirrors B and C come into play:
Finally, the semi-mirror D :
Remember: when we conducted this experiment without a sensor , outcomes # 1 and # 3 "neutralized" each other, because their corresponding configurations were identical. But now they are not identical - and all thanks to the sensor S. The squares of the amplitude modules of all four configurations are equal, and if you actually conducted this experiment, you would be convinced that both detectors work with the same frequency. ( If I did not mess up anything, of course. Personally, I did not conduct an experiment.)
The same will happen if we are indifferent to the state of the sensor. The laws of physics are just as indifferent to our thoughts.
The same thing happens if we do not even bother to check whether the photon flew through S. Configurations # 1 and # 3 are different - nothing else is needed.
The same will happen if we do not know at all about the existence of S.
The same will happen if an experiment is conducted in space, and S signals its state by sending a single photon in one direction, if it was in the
(But the same will not happen if S has a sufficiently large length in the configuration space. In this case, the photon's impact on S may not be enough to form a separate outcome. I just wanted to remind you that the configuration space is in fact continuous but not discretely.)
And now let's try to imagine what the person who is conducting the experiment like this thinks about if he has no idea about amplitudes and configurations.
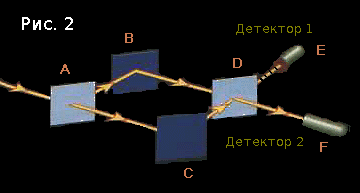
Our experimenter discovers that a) photons do not want to come to the first detector, and b) photons suddenly start to come to both detectors if one of the paths is blocked, but they are never separated. Hm
First, he believes that he is dealing with particles - after all, everything he observes is individual photons, each of which is (as he believes) in a strictly defined position at each moment in time. This is logical, albeit incorrect.
Secondly, he is convinced of the existence of a certain ... mysterious phenomenon ... which prevents the photon from appearing in the first detector. For this it is extremely important that the photon be able to appear in any of the detectors. Even if in the end he always chooses the second.
The cunning photon not only wants to be not obstructed - he also knows that the path is blocked, not even following it . What the hell is going on here?
Our experimenter decides to place the sensor between A and C in order to track which path the photon chooses each time.

And the mysterious phenomenon is blown away like a wind.
From such a paranoid and not be long.
In the twenty-first century, we already guessed that the “knowledge” of what happened to the photon is equivalent to a change in the position of the septillons of particles in our brain. If even one photon, released by the sensor in an unknown direction, is enough to make the configurations different and prevent the amplitudes from reducing, then a complex measuring device with which we will catch the photon is definitely enough.
But if you did not think of all this, your deeds are bad. Your thoughts are likely to go in a slightly different direction.
A photon does not just want to have the physical ability to go in both ways, because the sensor is completely transparent to it. Everything is much worse. Photon does not want you to know where he is and what he does.
If you know for sure that the photon has flown here , all other possibilities will become somewhat implausible . This prevents the photon no less than the real obstacle in its path. What is important is not what happened, but what could have happened. What you know - or rather, what you can theoretically know - is the determining factor.
Urgently in the room! Conscious understanding can influence experimental results! Mind is still primary!
Y-yes. Was it really so difficult to notice that a simple stone, “observing” the experiment, has the same effect on him? Perhaps stones have consciousness too?
However, in hindsight, everyone is smart. Do you think that you would be better off than John von Neumann if you lived at that time? The main thing at the time was that the theory, even if it was delusional, gave correct predictions; do not repair what is not broken and everything will be fine.
← read the first part
← read the first part
Configurations as combinations
One of the key points in quantum mechanics is that configurations always describe the state of more than one particle. Look: this time we will slightly complicate the experiment from the first article, at the same time sending two photons to D - from points B and C.

')
The initial configuration is “the photon flies from B to D , and the photon flies from C to D ”. Like last time, we will assume that its amplitude is equal to (-1 + 0 i ).
In D there is a semi-silvered mirror already familiar to us, which multiplies the amplitude by 1 when a photon is reflected, and by - i - when a photon passes ( i was in the original, but this is not quite true - approx. Lane ).
Consider four cases:
- Both photons reflected. The amplitude, equal to (−1 + 0 i ) × - i × - i = (1 + 0 i ), counts the configuration “the photon flies from D to E , and the photon flies from D to F ”.
- A photon flying from B is reflected; the photon flying from C flew by. Amplitude equal to (−1 + 0 i ) × - i × 1 = (0 + i ), the “two photons fly from D to E ” configuration counts.
- A photon flying from B is flying; photon flying from C reflected. The amplitude, equal to (−1 + 0 i ) × 1 × - i = (0 + i ), counts the configuration “two photons fly from D to F ”.
- Both photons flew. The amplitude equal to (−1 + 0 i ) × 1 × 1 = (−1 + 0 i ) is counted as “the photon flies from D to E , and the photon flies from D to F ”.
Please note that completely different situations in the first and fourth cases led to the same resulting configuration! Therefore, when we consider the final configuration value “photon flies to E , and photon flies to F ”, we will get (1 + 0 i ) + (−1 + 0 i ) = 0. And this means that this will never happen . Both detectors cannot work at the same time.
One important lesson to be learned from this experiment: photons are indistinguishable . If there were even the smallest difference between the two photons, the result of the experiment would be completely different.
In the classical model of the world, where amplitudes can be considered as probabilities, everyone is free to choose the way of grouping outcomes. Let me explain: I could consider all four outcomes described above as different; could distinguish only two outcomes (“each detector arrives in a photon” and “both photons arrive in one detector”); could do something else. And nothing would have changed. Similarly, if I need to calculate the probability that odd numbers fall out on two dice, I can compose a sign of 36 possible throw results — and I can immediately divide the faces into even and odd numbers and reduce the number of outcomes to four.
Why doesn't this work in a quantum model? Because the probabilities of events nonlinearly depend on amplitudes, and the sum square, as is known, cannot be replaced by the sum of squares:
((2 + i ) + (1 + - i )) 2 = (3 + 0 i ) 2 = 3 2 + 0 2 = 9
(2 + i ) 2 + (1 + - i ) 2 = (2 2 + 1 2 ) + (1 2 + (−1) 2 ) = (4 + 1) + (1 + 1) = 7
From this it follows that we can experimentally establish which configurations are different and which ones are not. In particular, these configurations are identical:
- “A photon from B is reflected in D and flies to E ; photon C is reflected in D and flies in F ”;
- “A photon from B flies through D to E ; photon C flies through D to F ".
And here is the second important lesson (which I hinted in the first paragraph, and which I will talk about in detail later): the laws of quantum mechanics are not applicable to individual particles . The strategy "divide and conquer" does not work here. This is a great temptation - without much difficulty to consider the behavior of each elementary particle, and then in some way put together a coherent picture of the world from pieces of a mosaic ... But it is this approach that for so many years inhibited the development of quantum mechanics.
Different configurations
Immediately take the bull by the horns. When are the two configurations different?
To answer this question, we will conduct the following experiment:

At point S is the sensor. The only thing he does is transfer to another state when a photon passes through it. We assume that at the beginning of the experiment, the sensor is in the
So, the initial configuration:
- “The photon flies toward A ; S in the state
”= (−1 + 0 i )
What happens after the photon arrives at A ? In the previous version of this experiment - without a sensor - the possible configurations were “photon flying from A to B ” with amplitude i and “photon flying from A to C ” with amplitude −1. But since each configuration describes the complete state of the system, we must include the state of the sensor in their descriptions. So:
- “The photon flies from A to B ; S is in the state of
”= (0 + i ) - “The photon flies from A to C ; S in
state ”= (−1 + 0 i )
Now mirrors B and C come into play:
- “The photon flies from B to D ; S in the state
”= (−1 + 0 i ) - “The photon flies from C to D ; S in
state ”= (0 + i )
Finally, the semi-mirror D :
- “The photon flies from D to E ; S is in the state of
”= (0 + i ) - “The photon flies from D to F ; S in the state
”= (−1 + 0 i ) - “The photon flies from D to E ; S in
state ”= (0 + i ) - “The photon flies from D to F ; S in
state ”= (1 + 0 i )
Remember: when we conducted this experiment without a sensor , outcomes # 1 and # 3 "neutralized" each other, because their corresponding configurations were identical. But now they are not identical - and all thanks to the sensor S. The squares of the amplitude modules of all four configurations are equal, and if you actually conducted this experiment, you would be convinced that both detectors work with the same frequency. ( If I did not mess up anything, of course. Personally, I did not conduct an experiment.)
The same will happen if we are indifferent to the state of the sensor. The laws of physics are just as indifferent to our thoughts.
The same thing happens if we do not even bother to check whether the photon flew through S. Configurations # 1 and # 3 are different - nothing else is needed.
The same will happen if we do not know at all about the existence of S.
The same will happen if an experiment is conducted in space, and S signals its state by sending a single photon in one direction, if it was in the
(But the same will not happen if S has a sufficiently large length in the configuration space. In this case, the photon's impact on S may not be enough to form a separate outcome. I just wanted to remind you that the configuration space is in fact continuous but not discretely.)
And now let's try to imagine what the person who is conducting the experiment like this thinks about if he has no idea about amplitudes and configurations.

Our experimenter discovers that a) photons do not want to come to the first detector, and b) photons suddenly start to come to both detectors if one of the paths is blocked, but they are never separated. Hm
First, he believes that he is dealing with particles - after all, everything he observes is individual photons, each of which is (as he believes) in a strictly defined position at each moment in time. This is logical, albeit incorrect.
Secondly, he is convinced of the existence of a certain ... mysterious phenomenon ... which prevents the photon from appearing in the first detector. For this it is extremely important that the photon be able to appear in any of the detectors. Even if in the end he always chooses the second.
The cunning photon not only wants to be not obstructed - he also knows that the path is blocked, not even following it . What the hell is going on here?
Our experimenter decides to place the sensor between A and C in order to track which path the photon chooses each time.

And the mysterious phenomenon is blown away like a wind.
From such a paranoid and not be long.
In the twenty-first century, we already guessed that the “knowledge” of what happened to the photon is equivalent to a change in the position of the septillons of particles in our brain. If even one photon, released by the sensor in an unknown direction, is enough to make the configurations different and prevent the amplitudes from reducing, then a complex measuring device with which we will catch the photon is definitely enough.
But if you did not think of all this, your deeds are bad. Your thoughts are likely to go in a slightly different direction.
A photon does not just want to have the physical ability to go in both ways, because the sensor is completely transparent to it. Everything is much worse. Photon does not want you to know where he is and what he does.
If you know for sure that the photon has flown here , all other possibilities will become somewhat implausible . This prevents the photon no less than the real obstacle in its path. What is important is not what happened, but what could have happened. What you know - or rather, what you can theoretically know - is the determining factor.
Urgently in the room! Conscious understanding can influence experimental results! Mind is still primary!
Y-yes. Was it really so difficult to notice that a simple stone, “observing” the experiment, has the same effect on him? Perhaps stones have consciousness too?
However, in hindsight, everyone is smart. Do you think that you would be better off than John von Neumann if you lived at that time? The main thing at the time was that the theory, even if it was delusional, gave correct predictions; do not repair what is not broken and everything will be fine.
← read the first part
Source: https://habr.com/ru/post/173783/
All Articles