Needle, thread and pi

This post will help you get out of a rather delicate situation. Let's say you are locked in a room, you have a skein of threads and a needle, and you are strongly demanded to calculate the approximate value of Pi using only these objects, well, anything can happen, you know. So, today, while listening to a course on the matan of the University of Pennsylvania on a course , I suddenly learned how to do it. That's what I could not have imagined, is the fact that the number Pi is hidden here. It turned out that the roots of this question go back to the 18th century, when Georges-Louis Leclerc de Buffon set himself the following task : “Suppose the floor is made of wooden strips of two colors, they alternate; What is the probability that the abandoned needle will fall so that it will cross the line of joining of two strips? ”Simulation of this process and the answer to the question can be found under the cut.

Simulation

In order not to spoil the intrigue, let's start with the experiment. So, we have a set of needles of length L and a skein of green. Apply to the surface a number of parallel segments of the same length at a distance L from each other.
')


Kin on this field 100 needles.



Perhaps a little. Add another 900 and mark those needles that cross the thread in red.



Suppose we threw not all needles at once, but one at a time, and recorded at each step the ratio of the number of needles caught on the thread to the total number of abandoned needles, thereby obtaining an increasing approximation of the likelihood that the needle will fall across the thread .



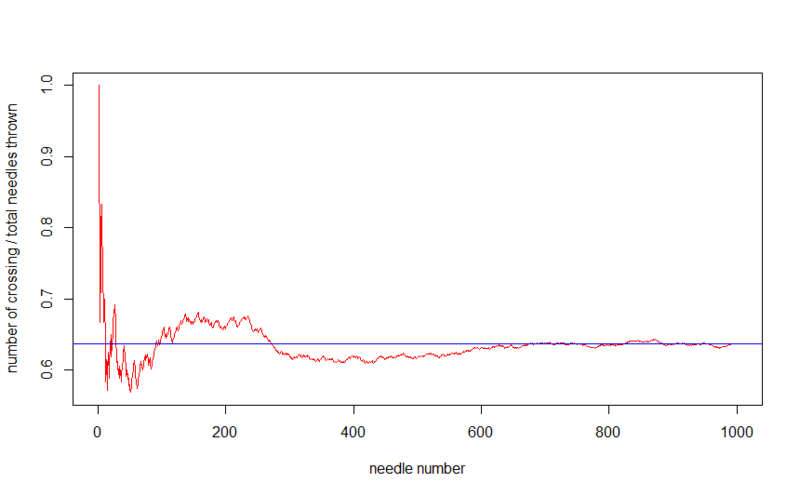
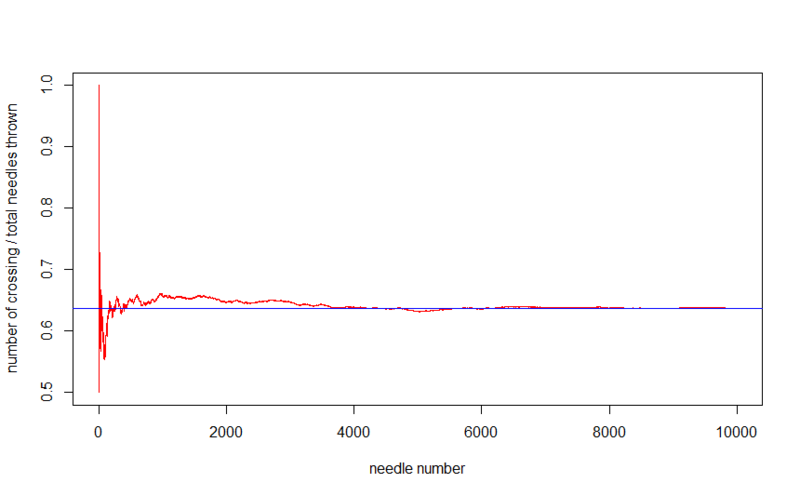
If you throw 10,000 needles, the picture will be more accurate.



And now we will make the following transformation: we will divide the two into each number of the series obtained.



For 10,000 needles is more accurate.



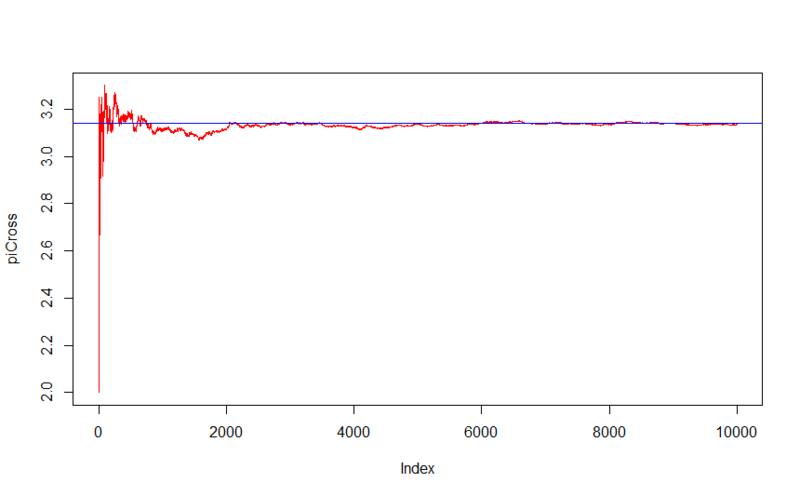
If we find the average of the last five thousand members of the series, we get 3.141685 , while pi is 3.141593 .

In general, it is no secret for anyone that the last row converges to the number Pi . But how could this happen? I learned this at the age of 28 from the above course. Dip in matan.

Theory

We will consider the needle and the line nearest from it to the right. The distance from the left end of the needle is denoted by h , the angle of deviation from the line is a .



Obviously, the length of the opposite leg from the angle a will be equal to the sine of the angle multiplied by the length of the hypotenuse. Then we can say that if h is less than or equal to the leg opposite the angle a , then the needle crosses the thread. Draw a graph:




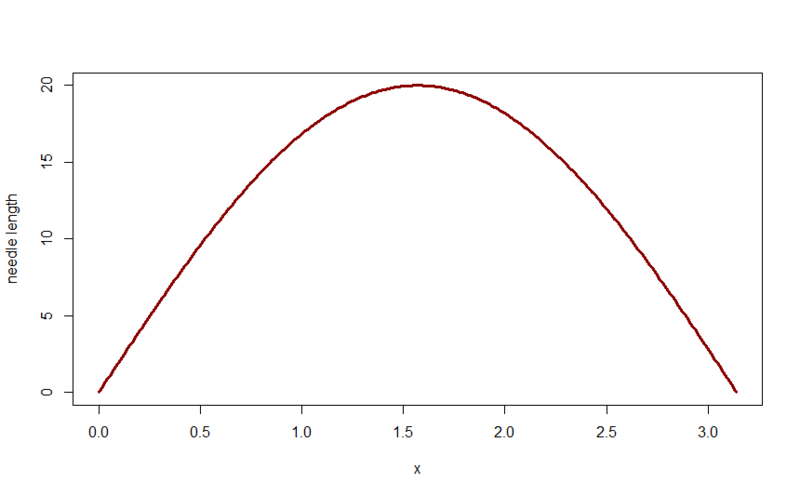
If we count for each abandoned needle h and a and mark these points in the previous graph, the picture will be as follows:



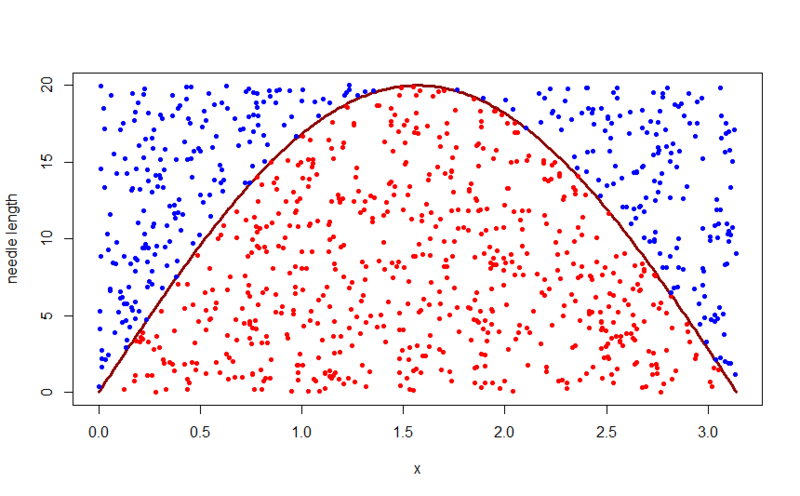
Thus, the probability that the needle crosses the thread will be equal to the ratio of the area of ​​the figure under the graph to the area of ​​the rectangle, i.e. Pi multiplied by the length of the needle.



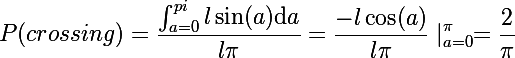
From here it turns out the desired approximation of the number Pi , which was shown by the experience in the first part.

Links

• Matan University of Pennsylvania course
• Buffon's needle problem