
A QR code is a monochrome picture in which some devices (for example, a smartphone with a special application) recognize the text. This text can be not only a simple phrase, but, although it is not included in the official specification, a link, a phone number or a business card. Such codes are most often used to encode a link and print it on a poster or business card.
This article is a detailed instruction on creating a QR code with examples at each step, which requires you to have only basic skills in working with binary data and mastering any programming language (if you want to create an automatic QR code generator).
')
The basis of this article is taken by the cycle of articles "QR Code Demystified" by Jason Brown (Jason Brown). There are many nuances in these articles that have caused me some problems. All these nuances are taken into account and mentioned here.
The process of generating a QR code is divided into several clear steps:
- Encoding data.
- Add service information and fill.
- The division of information into blocks.
- Creating correction bytes.
- Combining blocks.
- Placing information on the QR code.
Data coding
The QR code supports several ways of encoding data, depending on which characters are used: digital, alphanumeric, kanji (Chinese-Japanese hieroglyphs) and byte-coding. Digital coding implies using only numbers from 0 to 9, alphanumeric - capital letters of the Latin alphabet, numbers and symbols $% + + -. /: And a space, I will not consider kanji, and encoding bytes are not required at all. First you need to create an empty bit sequence, which will be filled further.
Digital coding
This type of encoding requires 10 bits by 3 characters. The entire sequence of characters is divided into groups of 3 digits, and each group (a three-digit number) is translated into a 10-bit binary number and added to the sequence of bits. If the total number of characters is not a multiple of 3, then if at the end there are 2 characters left, the resulting two-digit number is encoded with 7 bits, and if 1 character, then 4 bits.
For example, there is the string "12345678" that needs to be encoded. We divide it into numbers: 123, 456 and 78, then we translate each of them into binary form: 0001111011, 0111001000 and 1001110, and combine it into one stream: 000111101101110010001001110.
Alphanumeric encoding
In this case, 2 characters require 11 bits of information. The input stream of characters is divided into groups of 2, in the group each character is encoded according to the table below, the value of the first character in the group is multiplied by 45 and added to the value of the second character. The resulting number is converted to an 11-bit binary number and added to the bit sequence. If the last group contains 1 character, then its value is immediately encoded with a 6-bit number and added to the bit sequence.
Table 1. Values of characters in alphanumeric coding.| 0 | one | 2 | 3 | four | five | 6 | 7 | eight | 9 | A | B | C | D | E |
| 0 | one | 2 | 3 | four | five | 6 | 7 | eight | 9 | ten | eleven | 12 | 13 | 14 |
| F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T |
| 15 | sixteen | 17 | 18 | nineteen | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| U | V | W | X | Y | Z | Space | $ | % | * | + | - | . | / | : |
| thirty | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 |
For example, the string "HELLO" is encoded as follows. We divide into groups: HE, LL, O; we find the corresponding value of the symbols in each group: (17, 14), (21, 21), (24); we find the value for each group: 17 * 45 + 14 = 779, 21 * 45 + 21 = 966, 24 = 24; translate each value into a binary form: 779 = 01100001011, 966 = 01111000110, 24 = 011000; and combine it all into one sequence of bits: 0110000101101111000110011000.
Byte coding
This is a universal encoding method that can encode any characters. The only drawback of the method is the relatively low information density. In this case, the text is encoded in any encoding (recommended in UTF-8) and the resulting sequence of bytes is taken unchanged.
For example, the string "Habr", encoded UTF-8 encoding, a byte consists of the following: 11010000, 10100101, 11010000, 10110000, 11010000, 10110001, 11010001 and 10000000. They just need to be combined into a single bit stream: 1101000010100101110100001011000011010000101100011101000110000000.
Add service information
At this stage, it is necessary to determine the level of correction: the higher this level, the higher the permissible level of damage to the image and the less information with an equal size. There are 4 levels of correction in total: L (maximum 7% damage is acceptable), M (15%), Q (25%) and H (30%). Level M is most often used. If you want to add a picture to a QR code (there are several articles on this topic on Habré), then use level H.
Another property of the QR code is its version (the larger it is, the larger the size). There are 40 versions in total. The version number depends on the amount of information encoded and on the level of correction. Table 2 shows the maximum amount of useful information along with service information (in bits), which can be encoded in the QR code of this version. The version of our QR code is determined from this table.
Table 2. The maximum amount of information.Line - the level of correction, the column - the version number.
| one | 2 | 3 | four | five | 6 | 7 | eight | 9 | ten |
| L | 152 | 272 | 440 | 640 | 864 | 1088 | 1248 | 1552 | 1856 | 2192 |
| M | 128 | 224 | 352 | 512 | 688 | 864 | 992 | 1232 | 1456 | 1728 |
| Q | 104 | 176 | 272 | 384 | 496 | 608 | 704 | 880 | 1056 | 1232 |
| H | 72 | 128 | 208 | 288 | 368 | 480 | 528 | 688 | 800 | 976 |
| eleven | 12 | 13 | 14 | 15 | sixteen | 17 | 18 | nineteen | 20 |
| L | 2592 | 2960 | 3424 | 3688 | 4184 | 4712 | 5176 | 5768 | 6360 | 6888 |
| M | 2032 | 2320 | 2672 | 2920 | 3320 | 3624 | 4056 | 4504 | 5016 | 5352 |
| Q | 1440 | 1648 | 1952 | 2088 | 2360 | 2600 | 2936 | 3176 | 3560 | 3880 |
| H | 1120 | 1264 | 1440 | 1576 | 1784 | 2024 | 2264 | 2504 | 2728 | 3080 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | thirty |
| L | 7456 | 8048 | 8752 | 9392 | 10208 | 10960 | 11744 | 12248 | 13048 | 13880 |
| M | 5712 | 6256 | 6880 | 7312 | 8,000 | 8496 | 9024 | 9544 | 10136 | 10984 |
| Q | 4096 | 4544 | 4912 | 5312 | 5744 | 6032 | 6464 | 6968 | 7288 | 7880 |
| H | 3248 | 3536 | 3712 | 4112 | 4304 | 4768 | 5024 | 5288 | 5608 | 5960 |
| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| L | 14744 | 15640 | 16568 | 17528 | 18448 | 19472 | 20528 | 21616 | 22496 | 23648 |
| M | 11640 | 12328 | 13048 | 13800 | 14496 | 15312 | 15936 | 16816 | 17728 | 18672 |
| Q | 8264 | 8920 | 9368 | 9848 | 10288 | 10832 | 11408 | 12016 | 12656 | 13328 |
| H | 6344 | 6760 | 7208 | 7688 | 7888 | 8432 | 8768 | 9136 | 9776 | 10208 |
Adding service fields
At this point, the correction level should be selected and the version determined. Now it is necessary, before the bit sequence obtained in the previous paragraph, to add two fields at the beginning: the encoding method and the amount of data. The encoding method is a 4-bit field, which has the following values: 0001 for digital encoding, 0010 for alphanumeric and 0100 for byte-byte. The amount of data is the number of characters to be encoded, and for byte bytes, the number of bytes (and not the bits in the received sequence), represented as a binary number of a certain length (determined according to Table 3).
Table 3. The length of the data quantity field. | Version 1–9 | Version 10–26 | Version 27–40 |
| Digital | 10 bits | 12 bits | 14 bits |
| Alphanumeric | 9 bits | 11 bits | 13 bits |
| Byte byte | 8 bit | 16 bits | 16 bits |
For example, given a string of 100 bytes, encoded byte-byte, the correction level is M. The length of the bit sequence of this string is 800 bits. Using the table 2, you can determine that the best will use the 6th version. The length of the field that determines the amount of data in our case is 8 bits (Table 3). The field defining the encoding method is 0100, the data quantity field is 01100100 (100 in binary form). The result is a sequence of bits 010001100100 <original sequence>.
If the length of the received sequence of bits turned out to be more acceptable for the selected version, then the version should be increased by one and the service fields should be added anew.
The specification allows the use of mixed coding. This means that several data groups can be encoded in different ways and combined into one sequence. This is done as follows: <data encoding method 1> <data amount 1> <data 1> <data encoding method 2> <data amount 2> <data 2> and so on.
Filling
At this stage, we have a sequence of data bits, the number of bits in which is probably not a multiple of 8. We must add zeros so that its length becomes a multiple of 8. Now our sequence of bits can be divided into groups of 8 bits and represented as a sequence of bytes ( then we will do so). If the number of bits in the current byte sequence is less than that needed for the selected version, then it must be supplemented with alternating bytes 11101100 and 00010001. Thus, we have a sequence of bytes, the length of which corresponds to the selected version of the QR code.
Example. There is a sequence: <a sequence of bits whose length is a multiple of 8> 10101011101; we fill it with zeros so that its length becomes a multiple of 8: <a sequence of bits whose length is a multiple of 8> 10101011101 00000; Now suppose that its length is 104 bits, and for the selected version you need 128 bits, then you need to add 24 “fill” bits (3 bytes) to fill: <a sequence of bits that is a multiple of 8> 10101011101 00000 11101100 00010001 11101100. Done.
Information division into blocks
The sequence of bytes obtained in the previous step (hereinafter referred to as data) is divided into the number of blocks specified for the version and correction level, which is shown in Table 4. If the number of blocks is one, then this step can be skipped.
Table 4. The number of blocks.Line - the level of correction, the column - the version number.
| one | 2 | 3 | four | five | 6 | 7 | eight | 9 | ten |
| L | one | one | one | one | one | 2 | 2 | 2 | 2 | four |
| M | one | one | one | 2 | 2 | four | four | four | five | five |
| Q | one | one | 2 | 2 | four | four | 6 | 6 | eight | eight |
| H | one | one | 2 | four | four | four | five | 6 | eight | eight |
| eleven | 12 | 13 | 14 | 15 | sixteen | 17 | 18 | nineteen | 20 |
| L | four | four | four | four | 6 | 6 | 6 | 6 | 7 | eight |
| M | five | eight | 9 | 9 | ten | ten | eleven | 13 | 14 | sixteen |
| Q | eight | ten | 12 | sixteen | 12 | 17 | sixteen | 18 | 21 | 20 |
| H | eleven | eleven | sixteen | sixteen | 18 | sixteen | nineteen | 21 | 25 | 25 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | thirty |
| L | eight | 9 | 9 | ten | 12 | 12 | 12 | 13 | 14 | 15 |
| M | 17 | 17 | 18 | 20 | 21 | 23 | 25 | 26 | 28 | 29 |
| Q | 23 | 23 | 25 | 27 | 29 | 34 | 34 | 35 | 38 | 40 |
| H | 25 | 34 | thirty | 32 | 35 | 37 | 40 | 42 | 45 | 48 |
| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| L | sixteen | 17 | 18 | nineteen | nineteen | 20 | 21 | 22 | 24 | 25 |
| M | 31 | 33 | 35 | 37 | 38 | 40 | 43 | 45 | 47 | 49 |
| Q | 43 | 45 | 48 | 51 | 53 | 56 | 59 | 62 | 65 | 68 |
| H | 51 | 54 | 57 | 60 | 63 | 66 | 70 | 74 | 77 | 81 |
Determining the number of bytes in each block
To do this, you need to divide the entire number of bytes (you can determine the number of bytes in the data or divide the number from table 2 by eight) by the number of data blocks. If this number is not an integer, then it is necessary to determine the remainder of the division. This remainder determines how many blocks of all are added (such blocks, the number of bytes in which is one more than in the others). Contrary to expectations, the added blocks should not be the first blocks, but the last ones.
For example, for version 9 and the correction level M data quanta are 182 bytes, the number of blocks is 5. Sharing the number of data bytes by the number of blocks, we get 36 bytes and 2 bytes in the remainder. This means that the data blocks will have the following sizes: 36, 36, 36, 37, 37 (bytes). If there was no residue, all 5 blocks would be 36 bytes in size.
Filling the blocks
The block is filled with bytes from the data completely. When the current block is full, the queue moves to the next. Data bytes should be enough for all blocks, no more and no less.
Creating correction bytes
The following algorithm is applied to each data block (if the data block is one, then just to the data).
This algorithm is based on
the Reed – Solomon algorithm . The first thing to do is to determine how many bytes of correction should be created (table 5). By the number of correction bytes, the so-called generating polynomial is determined (Table 6). It is called a polynomial, because the original method uses a polynomial with the same coefficients.
Table 5. Number of correction bytes per block.Line - the level of correction, the column - the version number.
| one | 2 | 3 | four | five | 6 | 7 | eight | 9 | ten |
| L | 7 | ten | 15 | 20 | 26 | 18 | 20 | 24 | thirty | 18 |
| M | ten | sixteen | 26 | 18 | 24 | sixteen | 18 | 22 | 22 | 26 |
| Q | 13 | 22 | 18 | 26 | 18 | 24 | 18 | 22 | 20 | 24 |
| H | 17 | 28 | 22 | sixteen | 22 | 28 | 26 | 26 | 24 | 28 |
| eleven | 12 | 13 | 14 | 15 | sixteen | 17 | 18 | nineteen | 20 |
| L | 20 | 24 | 26 | thirty | 22 | 24 | 28 | thirty | 28 | 28 |
| M | thirty | 22 | 22 | 24 | 24 | 28 | 28 | 26 | 26 | 26 |
| Q | 28 | 26 | 24 | 20 | thirty | 24 | 28 | 28 | 26 | thirty |
| H | 24 | 28 | 22 | 24 | 24 | thirty | 28 | 28 | 26 | 28 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | thirty |
| L | 28 | 28 | thirty | thirty | 26 | 28 | thirty | thirty | thirty | thirty |
| M | 26 | 28 | 28 | 28 | 28 | 28 | 28 | 28 | 28 | 28 |
| Q | 28 | thirty | thirty | thirty | thirty | 28 | thirty | thirty | thirty | thirty |
| H | thirty | 24 | thirty | thirty | thirty | thirty | thirty | thirty | thirty | thirty |
| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| L | thirty | thirty | thirty | thirty | thirty | thirty | thirty | thirty | thirty | thirty |
| M | 28 | 28 | 28 | 28 | 28 | 28 | 28 | 28 | 28 | 28 |
| Q | thirty | thirty | thirty | thirty | thirty | thirty | thirty | thirty | thirty | thirty |
| H | thirty | thirty | thirty | thirty | thirty | thirty | thirty | thirty | thirty | thirty |
Table 6. Generating polynomials.| Number of correction bytes | Generating polynomial |
| 7 | 87, 229, 146, 149, 238, 102, 21 |
| ten | 251, 67, 46, 61, 118, 70, 64, 94, 32, 45 |
| 13 | 74, 152, 176, 100, 86, 100, 106, 104, 130, 218, 206, 140, 78 |
| 15 | 8, 183, 61, 91, 202, 37, 51, 58, 58, 237, 140, 124, 5, 99, 105 |
| sixteen | 120, 104, 107, 109, 102, 161, 76, 3, 91, 191, 147, 169, 182, 194, 225, 120 |
| 17 | 43, 139, 206, 78, 43, 239, 123, 206, 214, 147, 24, 99, 150, 39, 243, 163, 136 |
| 18 | 215, 234, 158, 94, 184, 97, 118, 170, 79, 187, 152, 148, 252, 179, 5, 98, 96, 153 |
| 20 | 17, 60, 79, 50, 61, 163, 26, 187, 202, 180, 221, 225, 83, 239, 156, 164, 212, 212, 188, 190 |
| 22 | 210, 171, 247, 242, 93, 230, 14, 109, 221, 53, 200, 74, 8, 172, 98, 80, 219, 134, 160, 105, 165, 231 |
| 24 | 229, 121, 135, 48, 211, 117, 251, 126, 159, 180, 169, 152, 192, 226, 228, 218, 111, 0, 117, 232, 87, 96, 227, 21 |
| 26 | 173, 125, 158, 2, 103, 182, 118, 17, 145, 201, 111, 28, 165, 53, 161, 21, 245, 142, 13, 102, 48, 227, 153, 145, 218, 70 |
| 28 | 168, 223, 200, 104, 224, 234, 108, 180, 110, 190, 195, 147, 205, 27, 232, 201, 21, 43, 245, 87, 42, 195, 212, 119, 242, 37, 9, 123 |
| thirty | 41, 173, 145, 152, 216, 31, 179, 182, 50, 48, 110, 86, 239, 96, 222, 125, 42, 173, 226, 193, 224, 130, 156, 37, 251, 216, 238, 40, 192, 180 |
Before executing the loop, it is necessary to prepare an array whose length is equal to the maximum of the number of bytes in the current block and the number of correction bytes, and fill its beginning with bytes from the current block, and the end with zeros.
The cycle described in this list is repeated as many times as the data bytes are contained in the current block.
- We take the first element of the array, save its value in the variable A and remove it from the array (all the following values are shifted one cell to the left, the last element is filled with zero).
- If A is zero, then skip the following steps (to the end of the list) and go to the next iteration of the loop.
- Find the corresponding number A number in table 8, put it in the variable B.
- Further, for the N first elements, where N is the number of correction bytes, i is the loop counter:
- It is necessary to add the value of B to the i-th value of the generating polynomial and write this sum in variable C (do not change the polynomial itself).
- If B is greater than 254, it is necessary to use its remainder when divided by 255 (255, not 256).
- Find the corresponding B value in Table 7 and perform bitwise addition modulo 2 (XOR, operator ^ in many programming languages) with the i-th value of the prepared array and write the obtained value into the i-th cell of the prepared array.
The first N bytes of the prepared array after this cycle are the correction bytes. For each data block, the corresponding byte correction block is obtained.
Nothing is clear? Me too. Look at the example and everything will become clear.
Table 7. Galois field.This table is a value for a Galois field of length 256. It can be automatically calculated.
| 0 | one | 2 | 3 | four | five | 6 | 7 | eight | 9 | ten | eleven | 12 | 13 | 14 | 15 |
| one | 2 | four | eight | sixteen | 32 | 64 | 128 | 29 | 58 | 116 | 232 | 205 | 135 | nineteen | 38 |
| sixteen | 17 | 18 | nineteen | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | thirty | 31 |
| 76 | 152 | 45 | 90 | 180 | 117 | 234 | 201 | 143 | 3 | 6 | 12 | 24 | 48 | 96 | 192 |
| 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 |
| 157 | 39 | 78 | 156 | 37 | 74 | 148 | 53 | 106 | 212 | 181 | 119 | 238 | 193 | 159 | 35 |
| 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 |
| 70 | 140 | five | ten | 20 | 40 | 80 | 160 | 93 | 186 | 105 | 210 | 185 | 111 | 222 | 161 |
| 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 |
| 95 | 190 | 97 | 194 | 153 | 47 | 94 | 188 | 101 | 202 | 137 | 15 | thirty | 60 | 120 | 240 |
| 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 |
| 253 | 231 | 211 | 187 | 107 | 214 | 177 | 127 | 254 | 225 | 223 | 163 | 91 | 182 | 113 | 226 |
| 96 | 97 | 98 | 99 | 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 |
| 217 | 175 | 67 | 134 | 17 | 34 | 68 | 136 | 13 | 26 | 52 | 104 | 208 | 189 | 103 | 206 |
| 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 | 126 | 127 |
| 129 | 31 | 62 | 124 | 248 | 237 | 199 | 147 | 59 | 118 | 236 | 197 | 151 | 51 | 102 | 204 |
| 128 | 129 | 130 | 131 | 132 | 133 | 134 | 135 | 136 | 137 | 138 | 139 | 140 | 141 | 142 | 143 |
| 133 | 23 | 46 | 92 | 184 | 109 | 218 | 169 | 79 | 158 | 33 | 66 | 132 | 21 | 42 | 84 |
| 144 | 145 | 146 | 147 | 148 | 149 | 150 | 151 | 152 | 153 | 154 | 155 | 156 | 157 | 158 | 159 |
| 168 | 77 | 154 | 41 | 82 | 164 | 85 | 170 | 73 | 146 | 57 | 114 | 228 | 213 | 183 | 115 |
| 160 | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 168 | 169 | 170 | 171 | 172 | 173 | 174 | 175 |
| 230 | 209 | 191 | 99 | 198 | 145 | 63 | 126 | 252 | 229 | 215 | 179 | 123 | 246 | 241 | 255 |
| 176 | 177 | 178 | 179 | 180 | 181 | 182 | 183 | 184 | 185 | 186 | 187 | 188 | 189 | 190 | 191 |
| 227 | 219 | 171 | 75 | 150 | 49 | 98 | 196 | 149 | 55 | 110 | 220 | 165 | 87 | 174 | 65 |
| 192 | 193 | 194 | 195 | 196 | 197 | 198 | 199 | 200 | 201 | 202 | 203 | 204 | 205 | 206 | 207 |
| 130 | 25 | 50 | 100 | 200 | 141 | 7 | 14 | 28 | 56 | 112 | 224 | 221 | 167 | 83 | 166 |
| 208 | 209 | 210 | 211 | 212 | 213 | 214 | 215 | 216 | 217 | 218 | 219 | 220 | 221 | 222 | 223 |
| 81 | 162 | 89 | 178 | 121 | 242 | 249 | 239 | 195 | 155 | 43 | 86 | 172 | 69 | 138 | 9 |
| 224 | 225 | 226 | 227 | 228 | 229 | 230 | 231 | 232 | 233 | 234 | 235 | 236 | 237 | 238 | 239 |
| 18 | 36 | 72 | 144 | 61 | 122 | 244 | 245 | 247 | 243 | 251 | 235 | 203 | 139 | eleven | 22 |
| 240 | 241 | 242 | 243 | 244 | 245 | 246 | 247 | 248 | 249 | 250 | 251 | 252 | 253 | 254 | 255 |
| 44 | 88 | 176 | 125 | 250 | 233 | 207 | 131 | 27 | 54 | 108 | 216 | 173 | 71 | 142 | one |
Table 8. Reverse Galois FieldThis table can be calculated from table 7.
| 0 | one | 2 | 3 | four | five | 6 | 7 | eight | 9 | ten | eleven | 12 | 13 | 14 | 15 |
| - | 0 | one | 25 | 2 | 50 | 26 | 198 | 3 | 223 | 51 | 238 | 27 | 104 | 199 | 75 |
| sixteen | 17 | 18 | nineteen | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | thirty | 31 |
| four | 100 | 224 | 14 | 52 | 141 | 239 | 129 | 28 | 193 | 105 | 248 | 200 | eight | 76 | 113 |
| 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 |
| five | 138 | 101 | 47 | 225 | 36 | 15 | 33 | 53 | 147 | 142 | 218 | 240 | 18 | 130 | 69 |
| 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 |
| 29 | 181 | 194 | 125 | 106 | 39 | 249 | 185 | 201 | 154 | 9 | 120 | 77 | 228 | 114 | 166 |
| 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 |
| 6 | 191 | 139 | 98 | 102 | 221 | 48 | 253 | 226 | 152 | 37 | 179 | sixteen | 145 | 34 | 136 |
| 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 |
| 54 | 208 | 148 | 206 | 143 | 150 | 219 | 189 | 241 | 210 | nineteen | 92 | 131 | 56 | 70 | 64 |
| 96 | 97 | 98 | 99 | 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 |
| thirty | 66 | 182 | 163 | 195 | 72 | 126 | 110 | 107 | 58 | 40 | 84 | 250 | 133 | 186 | 61 |
| 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 | 126 | 127 |
| 202 | 94 | 155 | 159 | ten | 21 | 121 | 43 | 78 | 212 | 229 | 172 | 115 | 243 | 167 | 87 |
| 128 | 129 | 130 | 131 | 132 | 133 | 134 | 135 | 136 | 137 | 138 | 139 | 140 | 141 | 142 | 143 |
| 7 | 112 | 192 | 247 | 140 | 128 | 99 | 13 | 103 | 74 | 222 | 237 | 49 | 197 | 254 | 24 |
| 144 | 145 | 146 | 147 | 148 | 149 | 150 | 151 | 152 | 153 | 154 | 155 | 156 | 157 | 158 | 159 |
| 227 | 165 | 153 | 119 | 38 | 184 | 180 | 124 | 17 | 68 | 146 | 217 | 35 | 32 | 137 | 46 |
| 160 | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 168 | 169 | 170 | 171 | 172 | 173 | 174 | 175 |
| 55 | 63 | 209 | 91 | 149 | 188 | 207 | 205 | 144 | 135 | 151 | 178 | 220 | 252 | 190 | 97 |
| 176 | 177 | 178 | 179 | 180 | 181 | 182 | 183 | 184 | 185 | 186 | 187 | 188 | 189 | 190 | 191 |
| 242 | 86 | 211 | 171 | 20 | 42 | 93 | 158 | 132 | 60 | 57 | 83 | 71 | 109 | 65 | 162 |
| 192 | 193 | 194 | 195 | 196 | 197 | 198 | 199 | 200 | 201 | 202 | 203 | 204 | 205 | 206 | 207 |
| 31 | 45 | 67 | 216 | 183 | 123 | 164 | 118 | 196 | 23 | 73 | 236 | 127 | 12 | 111 | 246 |
| 208 | 209 | 210 | 211 | 212 | 213 | 214 | 215 | 216 | 217 | 218 | 219 | 220 | 221 | 222 | 223 |
| 108 | 161 | 59 | 82 | 41 | 157 | 85 | 170 | 251 | 96 | 134 | 177 | 187 | 204 | 62 | 90 |
| 224 | 225 | 226 | 227 | 228 | 229 | 230 | 231 | 232 | 233 | 234 | 235 | 236 | 237 | 238 | 239 |
| 203 | 89 | 95 | 176 | 156 | 169 | 160 | 81 | eleven | 245 | 22 | 235 | 122 | 117 | 44 | 215 |
| 240 | 241 | 242 | 243 | 244 | 245 | 246 | 247 | 248 | 249 | 250 | 251 | 252 | 253 | 254 | 255 |
| 79 | 174 | 213 | 233 | 230 | 231 | 173 | 232 | 116 | 214 | 244 | 234 | 168 | 80 | 88 | 175 |
Example. Here I will represent all the bytes in the form of decimal numbers from 0 to 255. The original data block:
64 196 132 84 196 196 242 194 4 132 20 37 34 16 236 17The 2nd version with the correction level H is used. In this case, you need to create 28 bytes of correction (table 5) and use the generating polynomial (table 6):
168 223 200 104 224 234 108 180 110 190 195 147 205 27 232 201 21 43 245 87 42 195 212 119 242 37 9 123Create an array (prepared array) for 28 elements and fill it with data bytes:
64 196 132 84 196 196 242 194 4 132 20 37 34 16 236 17 0 0 0 0 0 0 0 0 0 0 0 0I will paint in detail the first step of the cycle, the rest in the form of a finished array. The first element of the array is 64. We remove it from the prepared array:
196 132 84 196 196 242 194 4 132 20 37 34 16 236 17 0 0 0 0 0 0 0 0 0 0 0 0 0In table 8, we find a match for it - 6; add 255 this number to each number of the generating polynomial:
174 229 206 110 230 240 114 186 116 196 201 153 211 33 238 207 27 49 251 93 48 201 218 125 248 43 15 129For each number of the generating polynomial, we find the correspondence in table 7:
241 122 83 103 244 44 62 110 248 200 56 146 178 39 11 166 12 140 216 182 70 56 43 51 27 119 38 23And we perform the operation of bitwise addition modulo 2 with the prepared array:
53 254 7 163 48 222 252 106 124 220 29 176 162 203 26 166 12 140 216 182 70 56 43 51 27 119 38 23Repeat these steps 16 times (16 bytes of data). The result will be the following correction bytes:
16 85 12 231 54 54 140 70 118 84 10 174 235 197 99 218 12 254 246 4 190 56 39 217 115 189 193 24All steps create correction bytes in the example.53 254 7 163 48 222 252 106 124 220 29 176 162 203 26 166 12 140 216 182 70 56 43 51 27 119 38 2388 135 181 100 195 209 67 42 120 103 75 204 49 123 234 32 53 11 134 32 223 208 235 172 113 56 81 191190 23 10 28 136 239 91 71 190 168 253 92 58 109 11 233 139 182 213 21 200 218 171 107 5 152 211 189228 45 104 109 161 181 177 87 87 252 124 67 75 80 92 99 7 5 181 129 178 139 129 144 140 151 52 1652 255 79 129 134 24 109 176 20 223 154 13 100 152 14 67 222 187 27 207 140 88 143 56 195 45 52 14326 93 185 156 60 134 13 37 17 219 197 54 203 22 176 174 81 245 0 114 47 71 202 248 80 160 251 151112 115 153 158 15 102 215 113 52 175 247 102 182 8 125 91 147 82 144 173 110 11 38 66 251 209 169 6115 78 183 5 213 230 209 248 21 105 76 199 65 7 16 193 91 121 47 32 241 12 49 154 134 191 143 9451 192 177 158 8 129 60 20 94 56 225 203 4 84 213 46 160 232 158 78 225 23 7 180 97 14 53 784 7 192 114 240 49 231 91 211 88 117 156 91 156 106 28 114 98 50 152 105 185 103 155 143 138 221 2790 14 140 115 176 11 131 74 31 13 39 199 42 189 39 147 164 92 245 157 142 220 138 15 164 75 82 232210 60 37 117 118 196 134 17 26 133 62 21 175 184 75 8 54 43 167 186 179 115 250 133 11 15 240 42172 41 101 21 220 18 111 12 96 8 155 252 130 250 45 22 214 227 54 41 81 116 201 160 144 41 179 9868 192 132 243 69 97 198 45 7 233 26 3 45 174 155 233 187 43 112 69 244 47 123 251 143 183 24 254230 218 208 22 221 33 116 11 144 80 182 27 186 140 25 253 238 61 30 163 135 206 41 202 86 90 48 3616 85 12 231 54 54 140 70 118 84 10 174 235 197 99 218 12 254 246 4 190 56 39 217 115 189 193 24
Combining blocks
We have several data blocks and as many blocks of correction bytes, they need to be combined into one stream of bytes. This is done as follows: from each data block, one byte of information is taken in turn, when the queue reaches the last block, a byte is taken from it, and the queue goes to the first block. This continues until bytes in each block run out. If there are no more bytes in the current block, then it is skipped (this happens when the usual blocks are already empty, and in the added blocks there is one byte). Similarly, you need to do with blocks of bytes correction. They are taken in the same order as the corresponding data blocks.
The result should be something like this: <1st byte of 1st data block> <1st byte of 2nd data block> ... <1st byte of nth data block> <2nd byte 1st data block> ... <(m - 1) -th byte of the 1st data block> ... <(m - 1) -th byte of the n-th data block> <m-th byte of k-th data block> ... <m-th byte of n-th data block> <1st byte of 1st correction byte block> <1st byte of 2nd correction byte block> ... <1st byte n th block of correction bytes> <2nd byte of 1st correction byte block> ... <lth byte of 1st correction byte block> ... <lth byte of nth correction byte block>. Here n is the number of data blocks, m is the number of bytes per data block of ordinary blocks, l is the number of correction bytes, k is the number of data blocks minus the number of padded data blocks (those with 1 more byte).
Placing information on the QR code
We have a byte sequence, which is ready to be placed on the canvas. Canvas consists of modules - elementary squares.

Basic elements
The size of the QR code depends only on the version. For the first version, this is 21 modules, and the sizes of the older versions are determined from table 9. In general, it shows the locations of the alignment patterns (more on that later), but the canvas size can be defined as the last number + 7 modules. I want to draw your attention that the indent, a frame of white modules 4 modules wide, is a full-fledged part of a QR code, and it cannot be ignored. Despite this, I indicate the width of the width of the part with black modules and start the report with its upper left corner ((0, 0) - the upper left module of the upper left search pattern).
Table 9. The location of the leveling patterns.The top line is the version number.
| one | 2 | 3 | four | five | 6 | 7 | eight |
| - | 18 | 22 | 26 | thirty | 34 | 6, 22, 38 | 6, 24, 42 |
| 9 | ten | eleven | 12 | 13 |
| 6, 26, 46 | 6, 28, 50 | 6, 30, 54 | 6, 32, 58 | 6, 34, 62 |
| 14 | 15 | sixteen | 17 | 18 |
| 6, 26, 46, 66 | 6, 26, 48, 70 | 6, 26, 50, 74 | 6, 30, 54, 78 | 6, 30, 56, 82 |
| 9 | 20 | 21 | 22 | 23 |
| 6, 30, 58, 86 | 6, 34, 62, 90 | 6, 28, 50, 72, 94 | 6, 26, 50, 74, 98 | 6, 30, 54, 78, 102 |
| 24 | 25 | 26 | 27 | 28 |
| 6, 28, 54, 80, 106 | 6, 32, 58, 84, 110 | 6, 30, 58, 86, 114 | 6, 34, 62, 90, 118 | 6, 26, 50, 74, 98, 122 |
| 29 | thirty | 31 | 32 |
| 6, 30, 54, 78, 102, 126 | 6, 26, 52, 78, 104, 130 | 6, 30, 56, 82, 108, 134 | 6, 34, 60, 86, 112, 138 |
| 33 | 34 | 35 | 36 |
| 6, 30, 58, 86, 114, 142 | 6, 34, 62, 90, 118, 146 | 6, 30, 54, 78, 102, 126, 150 | 6, 24, 50, 76, 102, 128, 154 |
| 37 | 38 | 39 | 40 |
| 6, 28, 54, 80, 106, 132, 158 | 6, 32, 58, 84, 110, 136, 162 | 6, 26, 54, 82, 110, 138, 166 | 6, 30, 58, 86, 114, 142, 170 |
Search patterns
These are patterns that are a black square measuring 3 by 3 modules, which is surrounded by a frame of white modules, which is surrounded by a frame of black modules, which is surrounded by a frame of white modules only from those sides where there is no indent. Search patterns are located in the upper and left corners (3 total).
Leveling patterns
Used from the 2nd version, they are a black square with a size of 1 to 1 module, which is surrounded by a frame of white modules, which is surrounded by a frame of black modules, as a result, this pattern has a size of 5 by 5. The places where the alignment patterns are located, are shown in table 9. More precisely, there are grid nodes vertically and horizontally, where the central modules of the patterns are located. For example, if the table says 6, 22, 38, this means that the centers of the modules should be located at the following points: (6, 6), (6, 22), (6, 38), (22, 6), (22 , 22), (22, 38), (38, 6), (38, 22), (38, 38). There is one important condition: the leveling patterns should not be layered on the search patterns. That is, when the version is greater than 6, there should be no alignment patterns at the points (first, first), (first, last) and (last, first) alignment patterns. In our example, these are (6, 6), (6, 38) and (38, 6).
Sync bands
Everything is simple here. The stripes start from the lower-right black module of the upper left search pattern and go, alternating black and white modules, down and to the right to opposite search patterns. When layered on the leveling pattern, it should remain unchanged.
Version code
These elements are used starting with the 7th version. The version code is duplicated in 2 places, and it is mirrored, that is, specifying the color of the module in coordinates (x, y), you can safely specify the same color in coordinates (y, x). The modules in these places are arranged in accordance with the figure below and table 10 (1 - black, 0 - white).
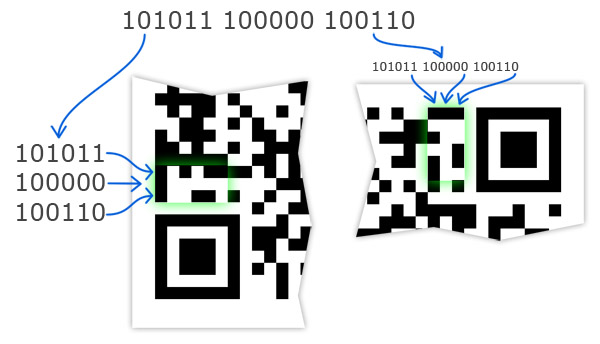
Table 10. Version codes.| Version | Version code |
| 7 | 000010 011110 100110 |
| eight | 010001 011100 111000 |
| 9 | 110111 011000 000100 |
| ten | 101001 111110 000000 |
| eleven | 001111 111010 111100 |
| 12 | 001101 100100 011010 |
| 13 | 101011 100000 100110 |
| 14 | 110101 000110 100010 |
| 15 | 010011 000010 011110 |
| sixteen | 011100 010001 011100 |
| 17 | 111010 010101 100000 |
| 18 | 100100 110011 100100 |
| nineteen | 000010 110111 011000 |
| 20 | 000000 101001 111110 |
| 21 | 100110 101101 000010 |
| 22 | 111000 001011 000110 |
| 23 | 011110 001111 111010 |
| 24 | 001101 001101 100100 |
| 25 | 101011 001001 011000 |
| 26 | 110101 101111 011100 |
| 27 | 010011 101011 100000 |
| 28 | 010001 110101 000110 |
| 29 | 110111 110001 111010 |
| thirty | 101001 010111 111110 |
| 31 | 001111 010011 000010 |
| 32 | 101000 011000 101101 |
| 33 | 001110 011100 010001 |
| 34 | 010000 111010 010101 |
| 35 | 110110 111110 101001 |
| 36 | 110100 100000 001111 |
| 37 | 010010 100100 110011 |
| 38 | 001100 000010 110111 |
| 39 | 101010 000110 001011 |
| 40 | 111001 000100 010101 |
Mask code and correction level
This code, as well as the previous one, is duplicated in 2 places: next to the upper left search pattern and next to the lower and right search patterns (the element has a break). In it, the mask code is ciphered in a special way (more on this later) and the code of the correction level. The finished codes are given in Table 11. The mask is determined at the very last step, when all the rest of the free space is filled with data. Due to the fact that the mask is selected on the basis of the best option (for this you need to go through all the masks), you will have to return more than once to adding the mask code and the level of correction. Do not add this item yet. The figure shows exactly where and in which direction the modules of this element are lined up, and also the module, which is always black, is marked in red.
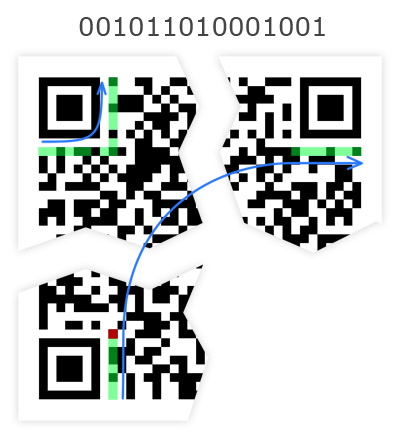
Table 11. Mask codes and level of correction.| Correction level | Mask code | Code |
| L | 0 | 111011111000100 |
| L | one | 111001011110011 |
| L | 2 | 111110110101010 |
| L | 3 | 111100010011101 |
| L | four | 110011000101111 |
| L | five | 110001100011000 |
| L | 6 | 110110001000001 |
| L | 7 | 110100101110110 |
| M | 0 | 10,1010000010010 |
| M | one | 101000100100101 |
| M | 2 | 101111001111100 |
| M | 3 | 101101101001011 |
| M | four | 100010111111001 |
| M | five | 100000011001110 |
| M | 6 | 100111110010111 |
| M | 7 | 100101010100000 |
| Q | 0 | 011010101011111 |
| Q | one | 011000001101000 |
| Q | 2 | 011111100110001 |
| Q | 3 | 011101000000110 |
| Q | four | 010010010110100 |
| Q | five | 010000110000011 |
| Q | 6 | 010111011011010 |
| Q | 7 | 010101111101101 |
| H | 0 | 001011010001001 |
| H | one | 001001110111110 |
| H | 2 | 001110011100111 |
| H | 3 | 001100111010000 |
| H | four | 000011101100010 |
| H | five | 000001001010101 |
| H | 6 | 000110100001100 |
| H | 7 | 000100000111011 |
Adding data
All the remaining free space on the canvas is divided into columns: every 2 modules, no matter what is in these modules, except for the vertical sync band, which is simply skipped. Filling starts from the bottom right corner, goes within the bounds from right to left, from bottom to top. If the current module is busy (for example, a sync stripe or an alignment pattern), then it is simply skipped. If the top of the bar is reached, the movement continues from the upper right corner of the bar, which is located to the left, and goes from top to bottom. Reaching the bottom, the movement continues from the lower right corner of the column, which is located to the left, and goes upwards. And so on, until all the free space is filled.

Filling takes place bit by bit from the data bytes, with 1 being the black module and 0 being the white. If there is not enough data, the remaining space is filled with zero modules.
In this case, one of the masks is superimposed on each module. The total number of masks is 8 pieces (from 0 to 7), their list is in table 12. If the expression from the table is zero, the color of the module is inverted, otherwise it remains unchanged. The mask applies only to data modules.
Table 12. Masks.X is a column, Y is a string,% is the remainder of a division, / is integer division.
| Mask number | Mask |
| 0 | (X + Y)% 2 |
| one | Y% 2 |
| 2 | X% 3 |
| 3 | (X + Y)% 3 |
| four | (X / 3 + Y / 2)% 2 |
| five | (X * Y)% 2 + (X * Y)% 3 |
| 6 | ((X * Y)% 2 + (X * Y)% 3)% 2 |
| 7 | ((X * Y)% 3 + (X + Y)% 2)% 2 |
The mask is chosen in different ways: some always use the same, others are random each time, but the specification insists that each mask is evaluated and the most optimal is chosen. The method with the assessment requires more time, but there is nothing terrible if an optimal mask is not chosen, so it is not necessary to use it, but I will still tell about it. The mask code and correction level (see above) depends on the selected mask; now is the time to add this element.
Choosing the best mask
This part is optional, and if you have already decided on the choice of mask and added data to the canvas, your QR code is ready.
The essence of this procedure is to generate a QR code with each of the eight masks, to charge each penalty points according to certain rules and choose a mask with the least amount of points. Remember that together with the data, the element of the mask code and the level of correction is added to the canvas again.
Rule 1
Horizontally and vertically for every 5 or more modules of the same color running in a row, the number of points equal to the length of this section is minus 2. In this and all other rules, the indent is not considered, everything is limited to the main field.

Rule 2
For each square of modules of the same color with a size of 2 by 2, 3 points are awarded.

Rule 3
For each sequence of modules CHBCHCHBCH, with 4 white modules on one side (or from 2 at once), 40 points are added (vertically or horizontally). Simply put, for these elements:

In our example, there are only 3 such elements, for which he gets 120 additional points (these elements need not intersect with the search pattern):

Rule 4
The number of points in this step depends on the ratio of the number of black and white modules. The closer it is to the 50% to 50% ratio, the better. The first thing to do is to divide the number of black modules by the total number of modules (again, the indent is not considered).
203 / 441 = 0.46032Then multiply the result by 100 and subtract 50.
0.46032 * 100 - 50 = -3.986Discard the decimal part and take the number modulo.
-3.986 -> 3Multiply the resulting number by 2.
3 * 2 = 6Add this number to the total number of penalty points.
Total
In the end, for each mask, you will get your number of penalty points, you will only have to choose the one with less points and your QR code is completely ready. As practice shows, the lower the mask number, the greater the likelihood that it will be the best, so for optimization you can choose the best mask not from all, but, for example, from 4.
Articles taken as a basis








