Wrestling ratings
The other day I read an interesting article about ratings. As a practical guide, I do not recommend using it (why see it in the comments to it), however, the reading material is interesting and gave me one thought.
Suppose we have a rating from 1 to 5. And some estimates are screwed up, some users have randomly set. How to filter the wheat from the chaff?
If you build a chart of the number of people who have made a certain assessment, then you can see approximately how many votes were spun. It is necessary, of course, to compare with other diagrams, but from this picture it is clear that part of the “fives” are twisted:

')
In general, a person can determine the cheating on the diagram, which means that the machine will also be able to.
The distribution of votes can be described by the beta distribution function .
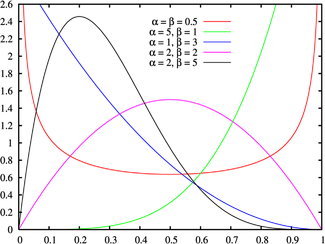
If in most cases the vote can be described by the beta function, but not in part, then some of the votes can be removed.

Thus, we will not exclude all bad voices, we will exclude some of the good ones. For articles with a small number of votes such manipulations are unacceptable.
The beta distribution has two parameters, alpha and beta. We also have two parameters: mean score (E) and variance (D) - a measure of the spread. From wikipedia it is known that.
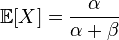
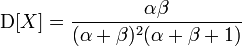
Now we solve the system of equations. It is long and tedious.
As a result, we can build a beta function. All estimates are higher than her, probable cheating. If someone will be interested in the sign for more.
Suppose we have a rating from 1 to 5. And some estimates are screwed up, some users have randomly set. How to filter the wheat from the chaff?
If you build a chart of the number of people who have made a certain assessment, then you can see approximately how many votes were spun. It is necessary, of course, to compare with other diagrams, but from this picture it is clear that part of the “fives” are twisted:

')
In general, a person can determine the cheating on the diagram, which means that the machine will also be able to.
The distribution of votes can be described by the beta distribution function .

If in most cases the vote can be described by the beta function, but not in part, then some of the votes can be removed.

Thus, we will not exclude all bad voices, we will exclude some of the good ones. For articles with a small number of votes such manipulations are unacceptable.
The beta distribution has two parameters, alpha and beta. We also have two parameters: mean score (E) and variance (D) - a measure of the spread. From wikipedia it is known that.
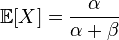
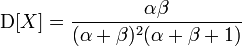
Now we solve the system of equations. It is long and tedious.
E = a / (a + b)
d = ab / ((a + b) ^ 2 * (a + b + 1))
replace a / (a + b) with E
d = bE / ((a + b) * (a + b + 1))
replace 1 / (a + b) with E / a
d = b * E ^ 2 / (a * (a + b + 1))
multiply both sides by (a * (a + b + 1))
d (a * (a + b + 1)) = b * E ^ 2
open brackets and swap
b * E ^ 2 = da ^ 2 + dab + da
subtract dab from both parts
b * E ^ 2-dab = da ^ 2 + da
b (E ^ 2-da) = da (a + 1)
b = da (a + 1) / (E ^ 2-da)
Let's go back to the first equation.
E = a / (a + b) => (a + b) = a / E => b = a / E -a
combine both equations
b = a / E -a = da (a + 1) / (E ^ 2-da)
a / E -a = da (a + 1) / (E ^ 2-da)
divide by a
1 / E -1 = d (a + 1) / (E ^ 2-da)
multiply by E (E ^ 2-da)
(1-E) (E ^ 2-da) = Ed (a + 1)
E ^ 2-da -E ^ 3 + Eda = Eda + Ed
Eda cut
E ^ 2-da -E ^ 3 = Ed
E ^ 2 -E ^ 3 -Ed = da
a = (E ^ 2 -E ^ 3 -Ed) / d
b = a / E -a = a (1 / E-1) = a (1-E) / E = (E ^ 2 -E ^ 3 -Ed) (1-E) / Ed = (E -E ^ 2 -d) (1-E) / d = (E -E ^ 2 -d - E ^ 2 + E ^ 3 + dE) / d
b = (E ^ 3-2E ^ 2 + E) / d + E -1
As a result, we can build a beta function. All estimates are higher than her, probable cheating. If someone will be interested in the sign for more.
Source: https://habr.com/ru/post/172339/
All Articles