Differential Evolution: Genetic Function Optimization Algorithm
On Habré there are many articles on evolutionary algorithms in general and genetic algorithms in particular. In such articles, the general structure and ideology of a genetic algorithm is usually described in more or less detail, and then an example of its use is given. Each such example includes some chosen variant of the procedure of crossing individuals, mutations and selection, and in most cases for each new task one has to invent his own version of these procedures. By the way, even the choice of representing the element of the decision space by the gene vector greatly influences the quality of the resulting algorithm and is essentially an art.
At the same time, many practical problems can easily be reduced to an optimization problem of finding the minimum of the function n of real variables, and for such a typical variant I would like to have a ready-made reliable genetic algorithm. Since even the definition of crossing operators and mutations for vectors consisting of real numbers is not entirely trivial, the “production” of a new algorithm for each such task turns out to be particularly time-consuming.
Under the cat is a brief description of one of the most well-known genetic algorithms of real optimization - the algorithm of differential evolution (Differential Evolution, DE). For complex problems of optimization of the function of n variables, this algorithm has such good properties that it can often be considered as a ready-made “building block” when solving many problems of identification and pattern recognition.
')
I will assume that the reader is familiar with the basic concepts used in the description of genetic algorithms, so I’ll go straight to the point, and in conclusion I will describe the most important properties of the DE algorithm.
A random set of N vectors from the space R n is selected as the initial population. The distribution of the initial population should be selected on the basis of the characteristics of the optimization problem to be solved - usually a sample of n -dimensional uniform or normal distribution is used with given mathematical expectation and variance.
At the next step of the algorithm, each individual X from the initial population is crossed with a randomly selected individual C , different from X. The coordinates of vectors X and C are considered as genetic traits. Before crossing, a special mutation operator is used — not the original, but the distorted genetic characteristics of the individual C are involved in the crossing:

Here, A and B are randomly selected members of the population, other than X and C. The parameter F defines so-called. mutation force - the amplitude of disturbances introduced into the vector by external noise. It should be particularly noted that, as noise that distorts the “gene pool” of the individual C , it is not the external source of entropy that is used, but the internal one — the difference between randomly selected representatives of the population. Below we will focus on this feature in more detail.
Crossing is as follows. The probability P is set with which the descendant T inherits the next (mutated) genetic trait from the parent C. The corresponding attribute from parent X is inherited with probability 1 - P. In fact, a binary random variable with a mathematical expectation P is played n times, and for its single values, the inheritance (transfer) of a distorted genetic trait from parent C (that is, the corresponding coordinates of vector C ' ) is performed, and for zero values, the genetic trait is inherited from parent X. As a result, a descendant vector T is formed .
The selection is carried out at each step of the functioning of the algorithm. After the formation of the descendant vector T , the objective function for it and for its “direct” parent X are compared. The new population is transferred to the one of the vectors X and T , on which the objective function reaches a smaller value (we are talking about the minimization problem). It should be noted here that the described selection rule guarantees the invariance of the population size during the operation of the algorithm.
In general, the DE algorithm is one of the possible "continuous" modifications of the standard genetic algorithm. At the same time, this algorithm has one significant feature, which largely determines its properties. The DE algorithm does not use an external random number generator as a noise source, but an “internal” one, implemented as the difference between randomly selected vectors of the current population. Recall that a set of random points selected from a certain general distribution is used as the initial population. At each step, the population is transformed by some rules and as a result, in the next step, a set of random points is again used as a source of noise, but some new distribution law corresponds to these points. Experiments show that, in general, the evolution of a population corresponds to the dynamics of a “swarm of midges” (ie, a random cloud of points) moving as a whole along the relief of an optimized function, repeating its characteristic features. In the case of falling into a ravine, the cloud takes the form of this ravine and the distribution of points becomes such that the expectation of the difference of two random vectors is directed along the long side of the ravine. This provides fast movement along narrow elongated ravines, while gradient methods under similar conditions are characterized by “wall-to-wall” vibrational dynamics. These heuristic considerations illustrate the most important and attractive feature of the DE algorithm — the ability to dynamically model the features of the relief of an optimized function, adjusting the distribution of the “built-in” noise source to them. This explains the remarkable ability of the algorithm to quickly pass complex ravines, ensuring efficiency even in the case of complex terrain.
For population size N , the value Q * n is usually recommended, where 5 <= Q <= 10 .
For the mutation force F, reasonable values are chosen from the segment [0.4, 1.0] , with a good initial value being 0.5 , but with a fast degeneration of the population far from the solution, the parameter F should be increased.
The probability of mutation P varies from 0.0 to 1.0 , and you should start with relatively large values ( 0.9 or even 1.0 ) to test the possibility of quickly obtaining a solution by random search. Then, the parameter values should be reduced to 0.1 or even 0.0 , when there is practically no variation in the population and the search turns out to be convergent.
Convergence is most affected by population size and mutational strength, and the probability of mutation serves to fine tune it.
The features of the DE method are well illustrated when running it on the standard test function of Rosenbrock

This function has an obvious minimum at the point x = y = 1 , which lies at the bottom of a long winding ravine with steep walls and a very flat bottom.
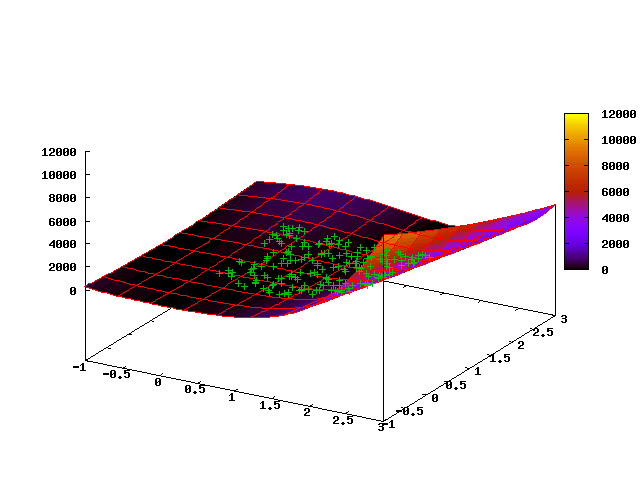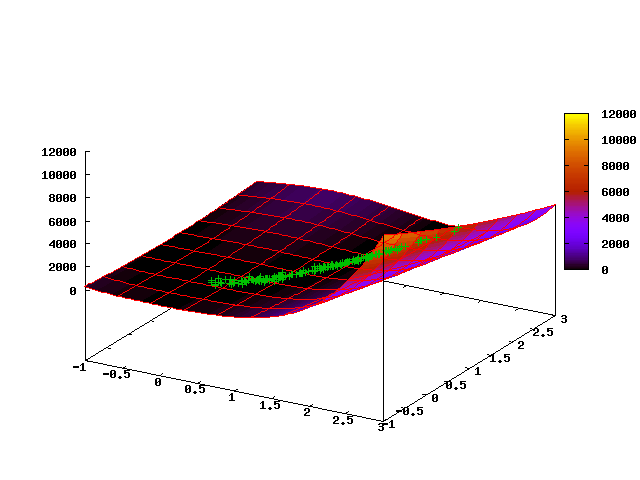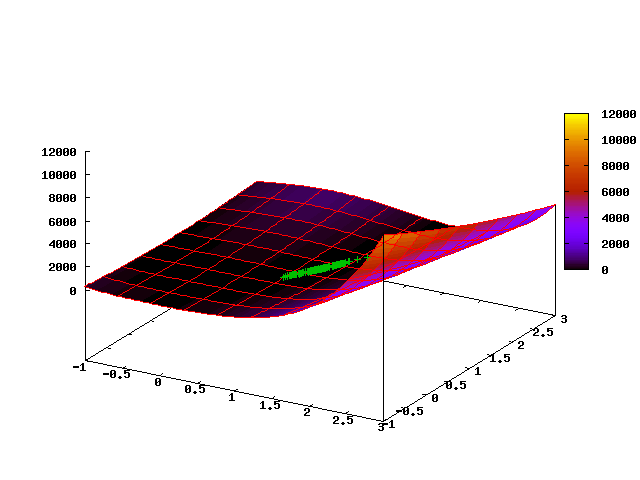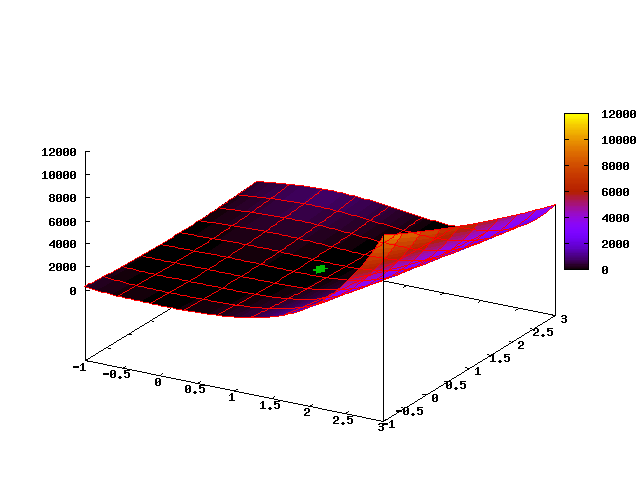
When running with a uniform initial distribution of 200 points per square [0, 2] x [0, 2] after 15 steps, we get the following distribution of the population:

It can be seen that the “cloud” of points is located along the bottom of the ravine and most mutations will lead to a shift of points along the bottom of the ravine, i.e. The method is well adapted to the features of the geometry of the solution space.
The following animated picture shows the evolution of a point cloud in the first 35 steps of the algorithm (the first frame corresponds to the initial uniform distribution):
At the same time, many practical problems can easily be reduced to an optimization problem of finding the minimum of the function n of real variables, and for such a typical variant I would like to have a ready-made reliable genetic algorithm. Since even the definition of crossing operators and mutations for vectors consisting of real numbers is not entirely trivial, the “production” of a new algorithm for each such task turns out to be particularly time-consuming.
Under the cat is a brief description of one of the most well-known genetic algorithms of real optimization - the algorithm of differential evolution (Differential Evolution, DE). For complex problems of optimization of the function of n variables, this algorithm has such good properties that it can often be considered as a ready-made “building block” when solving many problems of identification and pattern recognition.
')
I will assume that the reader is familiar with the basic concepts used in the description of genetic algorithms, so I’ll go straight to the point, and in conclusion I will describe the most important properties of the DE algorithm.
Generation of the initial population
A random set of N vectors from the space R n is selected as the initial population. The distribution of the initial population should be selected on the basis of the characteristics of the optimization problem to be solved - usually a sample of n -dimensional uniform or normal distribution is used with given mathematical expectation and variance.
Reproduction of descendants
At the next step of the algorithm, each individual X from the initial population is crossed with a randomly selected individual C , different from X. The coordinates of vectors X and C are considered as genetic traits. Before crossing, a special mutation operator is used — not the original, but the distorted genetic characteristics of the individual C are involved in the crossing:

Here, A and B are randomly selected members of the population, other than X and C. The parameter F defines so-called. mutation force - the amplitude of disturbances introduced into the vector by external noise. It should be particularly noted that, as noise that distorts the “gene pool” of the individual C , it is not the external source of entropy that is used, but the internal one — the difference between randomly selected representatives of the population. Below we will focus on this feature in more detail.
Crossing is as follows. The probability P is set with which the descendant T inherits the next (mutated) genetic trait from the parent C. The corresponding attribute from parent X is inherited with probability 1 - P. In fact, a binary random variable with a mathematical expectation P is played n times, and for its single values, the inheritance (transfer) of a distorted genetic trait from parent C (that is, the corresponding coordinates of vector C ' ) is performed, and for zero values, the genetic trait is inherited from parent X. As a result, a descendant vector T is formed .
Selection
The selection is carried out at each step of the functioning of the algorithm. After the formation of the descendant vector T , the objective function for it and for its “direct” parent X are compared. The new population is transferred to the one of the vectors X and T , on which the objective function reaches a smaller value (we are talking about the minimization problem). It should be noted here that the described selection rule guarantees the invariance of the population size during the operation of the algorithm.
Discussion features of the algorithm DE
In general, the DE algorithm is one of the possible "continuous" modifications of the standard genetic algorithm. At the same time, this algorithm has one significant feature, which largely determines its properties. The DE algorithm does not use an external random number generator as a noise source, but an “internal” one, implemented as the difference between randomly selected vectors of the current population. Recall that a set of random points selected from a certain general distribution is used as the initial population. At each step, the population is transformed by some rules and as a result, in the next step, a set of random points is again used as a source of noise, but some new distribution law corresponds to these points. Experiments show that, in general, the evolution of a population corresponds to the dynamics of a “swarm of midges” (ie, a random cloud of points) moving as a whole along the relief of an optimized function, repeating its characteristic features. In the case of falling into a ravine, the cloud takes the form of this ravine and the distribution of points becomes such that the expectation of the difference of two random vectors is directed along the long side of the ravine. This provides fast movement along narrow elongated ravines, while gradient methods under similar conditions are characterized by “wall-to-wall” vibrational dynamics. These heuristic considerations illustrate the most important and attractive feature of the DE algorithm — the ability to dynamically model the features of the relief of an optimized function, adjusting the distribution of the “built-in” noise source to them. This explains the remarkable ability of the algorithm to quickly pass complex ravines, ensuring efficiency even in the case of complex terrain.
Parameter selection
For population size N , the value Q * n is usually recommended, where 5 <= Q <= 10 .
For the mutation force F, reasonable values are chosen from the segment [0.4, 1.0] , with a good initial value being 0.5 , but with a fast degeneration of the population far from the solution, the parameter F should be increased.
The probability of mutation P varies from 0.0 to 1.0 , and you should start with relatively large values ( 0.9 or even 1.0 ) to test the possibility of quickly obtaining a solution by random search. Then, the parameter values should be reduced to 0.1 or even 0.0 , when there is practically no variation in the population and the search turns out to be convergent.
Convergence is most affected by population size and mutational strength, and the probability of mutation serves to fine tune it.
Numerical example
The features of the DE method are well illustrated when running it on the standard test function of Rosenbrock

This function has an obvious minimum at the point x = y = 1 , which lies at the bottom of a long winding ravine with steep walls and a very flat bottom.
When running with a uniform initial distribution of 200 points per square [0, 2] x [0, 2] after 15 steps, we get the following distribution of the population:

It can be seen that the “cloud” of points is located along the bottom of the ravine and most mutations will lead to a shift of points along the bottom of the ravine, i.e. The method is well adapted to the features of the geometry of the solution space.
The following animated picture shows the evolution of a point cloud in the first 35 steps of the algorithm (the first frame corresponds to the initial uniform distribution):

Links
- The home page of the algorithm contains many implementations and examples of use in different areas.
- Article in Dr. Dobb's Journal contains a very simple and understandable C language implementation, which can be taken as a basis when using the DE algorithm in your projects.
Source: https://habr.com/ru/post/171751/
All Articles