Esoteric language 4DL
The 4DL language was invented in 2001 by the author Cliff L. Biffle. As he himself explained, he invented it first, because before that languages with four-dimensional programs did not exist, and secondly, because four-dimensional space is quite difficult to understand, and we must give people the opportunity to train their brains.
Russian Wikipedia refers this language to the family of "fungeoid". These are languages that originate from the Befunge language, programs in which are written as symbols on a rectangular grid and can be executed in any direction. In 4DL, a four-dimensional grid is used to represent the program, and the directions for its implementation, respectively, are 8.
A 4DL program might look like this:
This program is written not in the "basic" language, but on its extension, but more on that later.
Besides the fact that the language 4DL is fungeoid, it is also stack. The only data object the program can work with is a stack of integers. The numbers, the entered characters are put into it, and the characters for printing are taken from it.
')
Here is the system of commands proposed by the author:
As an example of the program, the author cites "Hello, World!" (With at least three errors). Unfortunately, the language with such commands is not capable of anything that is noticeably more serious (if not increasing the size of the program many times), therefore, for a start, I decided to add a couple more commands to it:
Life has become much more fun. For example, here’s what a program looks like that prints the sum of numbers from an input string:
A few words about the recording of the program (these are already my fantasies - the author did not describe the input syntax).
The space in which the program is located is divided into two-dimensional layers in which the coordinates Z and T are constant. The symbols of each layer are written in the form of a rectangular table, starting with the angle X = Y = 0. If it is a character from ASCII-7 (with a code from 33 to 126), it is written explicitly. If not, its two-digit hexadecimal code is written. Space can be defined as 20 or double underscore. Characters are written through any number of spaces, the line with them begins with a space.
Rectangles are combined into a two-dimensional table. Horizontally there are layers with the same T value (consecutively: Z = 0, Z = 1, ...), vertically - columns with the same Z value. The lengths of the lines in the layers, the number of lines in the layer, the number of layers in the table row may differ - the missing cells will be filled with characters with code 0. The layers in the row of the table are separated by the characters || and the lines themselves - lines starting with a minus.
By default, execution starts at the cell (0,0,0,0) in the X + direction. The starting point can be redefined by inserting the line> x, y, z, t in the program (the numbers x, y, z and t are decimal).
The execution path of the above program in 4-dimensional space looks like this:
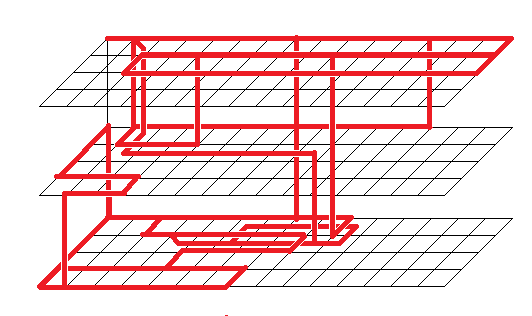
In addition to the cells through which the red line passes, there are some more data cells, but I decided not to show them.
It quickly becomes clear that the power of the 4DL language is entirely determined by the power of the underlying stack machine. So, if the digit capacity of the number in the stack is limited, then it is possible to implement those and only those algorithms that are implemented on finite state machines with stack memory. If the stack is allowed to place arbitrarily long numbers, and we have an operation to exchange two cells at the top of the stack, the language becomes Turing-complete — but the implementation of the Turing machine on it would be too slow (one operation would be at least 2 ^ 2 ^ N steps, where N is the size of the memory used). If the size of the number in the stack is limited, but there is an operation to read and modify cells in the depth of the stack (the offset from the vertex is also taken from the stack), then we get almost a TP-language — the available direct access memory will be limited.
In any case, the four-dimensionality of the program is almost not used, and any 4DL program can be embedded in two-dimensional space. Moreover, the string Y = 0 should be left for the executable code, Y = 1 - for the data, and the rest of the plane should be used to implement the transition commands. This option seems uninteresting.
The authors of the language Befunge stumbled upon the same problem of power limitations. To solve it, they added a mechanism for modifying memory cells to the language (which is correct), but they did this by allowing the cells to be accessed — both for reading and writing — by explicit coordinates. It seemed to me too strong a decision.
A more moderate version was proposed by the author of one of the 4DL language implementations - Bernhard Stoeckner. In the "extended" system of commands for its implementation, he offers, among other things, such commands:
It turns out that these commands are enough to make the Turing language complete even with an 8-bit stack cell (not to mention a 32-bit one). To prove this, let's go along the simplest path - we implement the Turing machine :)
The main problem we have is that we can read and change the contents of only the memory cells adjacent to the current point of the program. For a Turing machine, an infinite, or at least semi-infinite ribbon is needed, which means that the program must be self-modifying to communicate with distant cells.
The first idea was to realize the tape in the form of a “skyscraper”, in which each floor could support the commands “read the cell of the tape”, “change the contents of the cell”, “move up” and “move down”, and when it reaches the very top - run “construction platform, which grows in a parallel layer of reality, for the construction of a new floor. The task turned out to be solvable, but rather quickly managed to find a much simpler way.
It turns out that if you take a line of a program, for example, in the direction of X +, fill its left part with spaces, and somewhere put the “N” command (take a character from the stack and write it to the cell to the right), then put certain sequences of commands and data into the stack , and send the program to perform this line, the program can do what you need, and go back.
For example, the sequence [N, x, x, N] turns the string
in line
And if you then send the sequence [n, n, n, N, n] to this line, you get the string
- the leftmost "N" command will move to the cell to the left. Similarly, in two steps, you can execute the commands “move to the right”, “write the character in the next line” and “read the character from the next line”. The most convenient way is to work with a cell located two positions to the right of the cell where the “N” command is located.
A program that implements a Turing machine will consist of three parts. Layer T = 0 will be used for communication between the program and the tape. The program will be in the region T> 0, Z = 0 and will be a finite state machine (with memory), which will convert the current symbol on the tape into a pair (new symbol, direction of shift). We place the tape on the straight line Y = Z = T = 1, and the control program will occupy the area T> 0, Z = 1. The ribbon interface complements the program interface: for a pair (character, direction of shift), it changes the contents of the ribbon, shifts the carriage, and returns a new character pointed to by the carriage.
The purpose of the communication layer is the transfer of control from the program to the tape and back, as well as a debug print. In addition, this layer performs the start of the program (implementation costs: to start execution, you must explicitly push the contents of the cell to which the caret is pointing).
The current state of the program is stored by modifying the code. To perform the processing, the control is transferred to the point (2,3,0,1) in the direction of T +, and goes in a straight line filled with “T” commands with the exception of one cell corresponding to the current state. In this cell is the command "x" (go left). The program "goes on the right floor", changes the command "x" to "T", then analyzes the character at the top of the stack, puts the desired direction of movement and the new character on the stack, after which the side paths reach the "floor" corresponding to the new state, there puts in the cell (2,3,0, T) the command “x” and goes to the plane Z = T = 0, where it is transferred to control the tape.
Actually, everything. Here is an example of a program that doubles the number recorded on a tape. There are 7 states in the program, now the number 2 is on the tape (two ones).
If this program is run, it will print
Each triple of characters is a new character that needs to be left on the tape (0 or 1), the direction to move (0 - in place, 1 - to the left, 2 - to the right) and the character that appeared under the new carriage position. You can check that the program did everything correctly, and got the number 4.
With some effort, this implementation can also fit in 2D. But in 4 dimensions it is more pleasant to work - much more freedom.
You can slightly expand the language — add multiply, divide with remainder, and add 256 to the stack (for easier division of the number into bytes for writing to memory). True, there will be problems with negative numbers. Instead of 256, you can add the commands “split off the low byte” ([x] => [x & 0xff, x >> 8]) and “paste the low byte” ([x, y] => [x + (y << 8)]). But this will only make the language more convenient without changing its essence. It is more interesting to see what is in the language too much, and how best to use multidimensional memory.
For example:
By the way, a couple of four-dimensional (more precisely, multidimensional) languages were discovered at esolang. Both are BrainFuck dialects. But in one the carriage wanders through multidimensional memory, and the program looks like a line on the BF, and in the other way around - the program is multidimensional, but the memory is linear. The difference from 4DL is that in both cases, management and memory management are separate.
4DL page on esolang
Page from the author's blog
Interpreter site
Befunge and his dialects
Multi-dimensional brainfuck
Brainfuck with multi-dimensional program
Russian Wikipedia refers this language to the family of "fungeoid". These are languages that originate from the Befunge language, programs in which are written as symbols on a rectangular grid and can be executed in any direction. In 4DL, a four-dimensional grid is used to represent the program, and the directions for its implementation, respectively, are 8.
A 4DL program might look like this:
X , B / \ B + 2 B - < ? TB - T y __ 10 __ __ 7 __ __ A __ __ __ __ 07 __ __ ------------------------------------------------------------------ __ Y __ __ __ __ __ __ __ __ . __ x __ __ x || __ __ __ __ __ __ __ __ __ __ 20 __ __ __ __ __ t X __ __ __ q + 2 q - < ? Z q - Z || z __ __ __ __ __ __ __ __ . b . x __ __ x This program is written not in the "basic" language, but on its extension, but more on that later.
Besides the fact that the language 4DL is fungeoid, it is also stack. The only data object the program can work with is a stack of integers. The numbers, the entered characters are put into it, and the characters for printing are taken from it.
')
4DL programs
Here is the system of commands proposed by the author:
| X | Rotate pointer to command in X + direction |
| x | Rotate the pointer to the command in the direction of X- |
| Y | Rotate pointer to command in Y + direction |
| y | Rotate the pointer to the command in the direction of Y- |
| Z | Rotate pointer to command in Z + direction |
| z | Rotate the pointer to the command in the direction of Z- |
| T | Rotate the pointer to the command in the direction of T + |
| t | Rotate the pointer to the command in the direction of T- |
| P | Put the symbol from the adjacent cell on the X + side onto the stack |
| p | Put a symbol from the next cell on the stack from the side of X- |
| B | Put a symbol from the next cell on the stack on the Y + side |
| b | Put a symbol on the stack from the next cell on the side of Y- |
| D | Put a symbol on the stack from the next cell on the Z + side |
| d | Put a symbol from the next cell on the stack side of the Z- |
| Q | Put a symbol from the adjacent cell on the T + side onto the stack |
| q | Put a symbol from the next cell on the stack from the side of T- |
| + | Take the sum of two numbers on top of the stack, put the result on the stack |
| - | Take the difference of two numbers at the top of the stack, put the result on the stack |
| , | Enter a character from the keyboard and put it on the stack |
| . | Remove the character from the top of the stack and display |
| # | Jump over the next cell of the program |
| ? | Remove the number from the top of the stack, and if it is non-zero, then jump over the next cell of the program |
| 0 | Put number 0 on the stack |
| 2 | Put on the stack a copy of the number on top of it. |
| % | Finish the program |
As an example of the program, the author cites "Hello, World!" (With at least three errors). Unfortunately, the language with such commands is not capable of anything that is noticeably more serious (if not increasing the size of the program many times), therefore, for a start, I decided to add a couple more commands to it:
| \ | Change the contents of the two cells at the top of the stack |
| ^ | Remove the number from the top of the stack and do nothing with it (equivalent to 2- + or? XX - in the case of movement to the right) |
Life has become much more fun. For example, here’s what a program looks like that prints the sum of numbers from an input string:
0 X , D - 2 ? TD - 2 ? TD - Y || __ z __ 0D __ __ __ __ 13 __ __ __ __ 10 __ __ YDT ? 2 - DT ? 2 - D , x || __ __ __ 10 __ __ __ __ 13 __ __ __ __ 0D __ __ X - \ 2 2 + 2 + + 2 + + __ y ------------------- T t __ __ __ __ __ ^ __ __ __ __ x || __ t + y + ^ x __ __ __ __ ^ || __ y __ __ . B . B x D || 01 __ __ __ __ 0A __ 0D y \ + x __ X __ y ------------------- Y 0 x \ 0 ^ , x + x || __ __ __ __ __ Y __ __ . x \ __ y Z ? 2 \ - xy || __ __ __ X + X 2 ? ty D __ __ __ X + D \ y || 0A __ __ __ __ __ 3A X \ 2 ? y D - Y || __ __ __ __ __ 01 yt ? 2 - D \ x || __ __ __ __ __ 01 A few words about the recording of the program (these are already my fantasies - the author did not describe the input syntax).
The space in which the program is located is divided into two-dimensional layers in which the coordinates Z and T are constant. The symbols of each layer are written in the form of a rectangular table, starting with the angle X = Y = 0. If it is a character from ASCII-7 (with a code from 33 to 126), it is written explicitly. If not, its two-digit hexadecimal code is written. Space can be defined as 20 or double underscore. Characters are written through any number of spaces, the line with them begins with a space.
Rectangles are combined into a two-dimensional table. Horizontally there are layers with the same T value (consecutively: Z = 0, Z = 1, ...), vertically - columns with the same Z value. The lengths of the lines in the layers, the number of lines in the layer, the number of layers in the table row may differ - the missing cells will be filled with characters with code 0. The layers in the row of the table are separated by the characters || and the lines themselves - lines starting with a minus.
By default, execution starts at the cell (0,0,0,0) in the X + direction. The starting point can be redefined by inserting the line> x, y, z, t in the program (the numbers x, y, z and t are decimal).
The execution path of the above program in 4-dimensional space looks like this:

In addition to the cells through which the red line passes, there are some more data cells, but I decided not to show them.
Turing-full or not?
It quickly becomes clear that the power of the 4DL language is entirely determined by the power of the underlying stack machine. So, if the digit capacity of the number in the stack is limited, then it is possible to implement those and only those algorithms that are implemented on finite state machines with stack memory. If the stack is allowed to place arbitrarily long numbers, and we have an operation to exchange two cells at the top of the stack, the language becomes Turing-complete — but the implementation of the Turing machine on it would be too slow (one operation would be at least 2 ^ 2 ^ N steps, where N is the size of the memory used). If the size of the number in the stack is limited, but there is an operation to read and modify cells in the depth of the stack (the offset from the vertex is also taken from the stack), then we get almost a TP-language — the available direct access memory will be limited.
In any case, the four-dimensionality of the program is almost not used, and any 4DL program can be embedded in two-dimensional space. Moreover, the string Y = 0 should be left for the executable code, Y = 1 - for the data, and the rest of the plane should be used to implement the transition commands. This option seems uninteresting.
The authors of the language Befunge stumbled upon the same problem of power limitations. To solve it, they added a mechanism for modifying memory cells to the language (which is correct), but they did this by allowing the cells to be accessed — both for reading and writing — by explicit coordinates. It seemed to me too strong a decision.
4DL + and Turing machine
A more moderate version was proposed by the author of one of the 4DL language implementations - Bernhard Stoeckner. In the "extended" system of commands for its implementation, he offers, among other things, such commands:
| N | Put a character from the stack into the next cell on the side of X + |
| n | Put a character from the stack into the next cell from the side of X- |
| F | Put a character from the stack into the next cell on the Y + side |
| f | Put a character from the stack into the next cell from the side of Y- |
| G | Put a character from the stack into the next cell on the Z + side |
| g | Put a character from the stack into the next cell from the Z side |
| H | Put a symbol from the stack into the next cell on the T + side |
| h | Put a character from the stack into the next cell from the side of T- |
It turns out that these commands are enough to make the Turing language complete even with an 8-bit stack cell (not to mention a 32-bit one). To prove this, let's go along the simplest path - we implement the Turing machine :)
The main problem we have is that we can read and change the contents of only the memory cells adjacent to the current point of the program. For a Turing machine, an infinite, or at least semi-infinite ribbon is needed, which means that the program must be self-modifying to communicate with distant cells.
The first idea was to realize the tape in the form of a “skyscraper”, in which each floor could support the commands “read the cell of the tape”, “change the contents of the cell”, “move up” and “move down”, and when it reaches the very top - run “construction platform, which grows in a parallel layer of reality, for the construction of a new floor. The task turned out to be solvable, but rather quickly managed to find a much simpler way.
It turns out that if you take a line of a program, for example, in the direction of X +, fill its left part with spaces, and somewhere put the “N” command (take a character from the stack and write it to the cell to the right), then put certain sequences of commands and data into the stack , and send the program to perform this line, the program can do what you need, and go back.
For example, the sequence [N, x, x, N] turns the string
__ __ __ __ N
in line
__ __ __ __ NN x
And if you then send the sequence [n, n, n, N, n] to this line, you get the string
__ __ __ N nnx
- the leftmost "N" command will move to the cell to the left. Similarly, in two steps, you can execute the commands “move to the right”, “write the character in the next line” and “read the character from the next line”. The most convenient way is to work with a cell located two positions to the right of the cell where the “N” command is located.
A program that implements a Turing machine will consist of three parts. Layer T = 0 will be used for communication between the program and the tape. The program will be in the region T> 0, Z = 0 and will be a finite state machine (with memory), which will convert the current symbol on the tape into a pair (new symbol, direction of shift). We place the tape on the straight line Y = Z = T = 1, and the control program will occupy the area T> 0, Z = 1. The ribbon interface complements the program interface: for a pair (character, direction of shift), it changes the contents of the ribbon, shifts the carriage, and returns a new character pointed to by the carriage.
The purpose of the communication layer is the transfer of control from the program to the tape and back, as well as a debug print. In addition, this layer performs the start of the program (implementation costs: to start execution, you must explicitly push the contents of the cell to which the caret is pointing).
The current state of the program is stored by modifying the code. To perform the processing, the control is transferred to the point (2,3,0,1) in the direction of T +, and goes in a straight line filled with “T” commands with the exception of one cell corresponding to the current state. In this cell is the command "x" (go left). The program "goes on the right floor", changes the command "x" to "T", then analyzes the character at the top of the stack, puts the desired direction of movement and the new character on the stack, after which the side paths reach the "floor" corresponding to the new state, there puts in the cell (2,3,0, T) the command “x” and goes to the plane Z = T = 0, where it is transferred to control the tape.
Actually, everything. Here is an example of a program that doubles the number recorded on a tape. There are 7 states in the program, now the number 2 is on the tape (two ones).
Program
B __ Y || TX 2 Y 01 __ __ || __ __ __ P 0 __ __ __ || y \ . + b 2 x __ __ T . B x || __ __ 0 X . z __ Z __ __ __ __ || X 2 b + . \ y -------------------------------------------------------------------------------- __ __ __ __ __ 02 01 __ __ __ __ || Y t X # ? __ # \ __ __ N __ __ __ __ T __ __ X bb __ __ __ Y || __ __ T __ __ __ __ __ __ __ FF 00 01 01 00 X b F ? y BBY __ __ __ || N __ p y __ xx __ 02 00 T __ YT || __ __ y t __ fb __ __ __ __ __ x __ || __ __ T || N __ p || __ __ y __ __ __ __ __ __ __ __ x || XQQQQQQQQQQ y -------------------------------------------------------------------------------- __ __ __ __ __ 02 00 __ __ __ __ || __ __ t __ __ __ __ __ __ __ __ x __ T __ __ X bb __ Y __ __ || __ __ XBBBBBBBB y X b F ? y BBY __ __ __ || __ __ __ 01 # # F xx NN y __ T x __ 02 01 YT __ __ || __ __ __ t __ fb __ __ __ x __ __ __ || __ __ 2 || __ __ __ || __ __ __ || __ 00 01 # # B xx N 01 N -------------------------------------------------------------------------------- __ __ __ __ __ 01 01 __ __ __ __ || __ T __ __ X bb Y __ __ __ || X b F ? y BB __ Y __ __ || y __ T x __ 02 01 TY __ __ || __ __ __ t __ fb __ __ __ __ x __ __ || __ __ ? -------------------------------------------------------------------------------- __ __ __ __ __ 01 00 __ __ __ __ || __ T __ __ X bb __ Y __ __ || X b F ? y BBY __ __ __ || y __ T x __ 01 01 YT __ __ || __ __ t __ x t __ fb __ __ __ x __ __ __ || __ __ X ^ y -------------------------------------------------------------------------------- __ __ __ __ __ 02 01 __ __ __ __ || __ T __ __ X bb __ __ Y __ || X b F ? y BB __ Y __ __ || y __ T x __ 01 01 __ Y t __ || __ __ __ t __ fb __ __ __ __ x __ __ || __ __ P 01 -------------------------------------------------------------------------------- __ __ __ __ __ 01 00 __ __ __ __ || __ T __ __ X bb Y __ __ __ || X b F ? y BB __ __ __ Y || y __ T x __ 02 01 T __ __ Y || __ __ __ t __ fb __ __ __ __ __ __ x || __ __ - -------------------------------------------------------------------------------- __ __ __ __ __ __ __ __ __ __ __ || __ T __ __ % __ __ __ __ __ __ || X b F ? y BBY __ __ __ || y __ T x __ 00 00 Y __ __ __ || __ __ __ t __ fb __ __ __ x __ __ __ || __ __ ? -------------------------------------------------------------------------------- || || || __ __ __ __ N 01 xx N || __ __ t __ bbbbbx || __ __ XBBBBBB y || __ __ __ n N nn 01 n -------------------------------------------------------------------------------- || || || __ __ __ __ N 01 N xxn || __ __ t __ bbbbbbx || __ __ XBBBBBBB y || __ __ __ NNN __ 01 nn If this program is run, it will print
021 120 020 110 011 110 121 020 021 120 111 110 010 120 121 121 120 011 000
Each triple of characters is a new character that needs to be left on the tape (0 or 1), the direction to move (0 - in place, 1 - to the left, 2 - to the right) and the character that appeared under the new carriage position. You can check that the program did everything correctly, and got the number 4.
With some effort, this implementation can also fit in 2D. But in 4 dimensions it is more pleasant to work - much more freedom.
What's next?
You can slightly expand the language — add multiply, divide with remainder, and add 256 to the stack (for easier division of the number into bytes for writing to memory). True, there will be problems with negative numbers. Instead of 256, you can add the commands “split off the low byte” ([x] => [x & 0xff, x >> 8]) and “paste the low byte” ([x, y] => [x + (y << 8)]). But this will only make the language more convenient without changing its essence. It is more interesting to see what is in the language too much, and how best to use multidimensional memory.
For example:
- Is it possible to remove the stack and leave only an 8-bit or 32-bit battery?
- and if after that add fork (each process with its own battery)?
- and if instead of batteries, a parallel data layer is implemented, so that in each cell there will be one command and one data byte?
- ... and make all cells work in parallel and at the same time at the same time?
- It already turned out the scheme of Minecraft, or not yet?
And if not, then I will drink more ...
By the way, a couple of four-dimensional (more precisely, multidimensional) languages were discovered at esolang. Both are BrainFuck dialects. But in one the carriage wanders through multidimensional memory, and the program looks like a line on the BF, and in the other way around - the program is multidimensional, but the memory is linear. The difference from 4DL is that in both cases, management and memory management are separate.
References
4DL page on esolang
Page from the author's blog
Interpreter site
Befunge and his dialects
Multi-dimensional brainfuck
Brainfuck with multi-dimensional program
Source: https://habr.com/ru/post/170875/
All Articles