Notes on the implementation of hashCode () in Java
Often during interviews you have to ask about the hashCode () function.
I will not enumerate here all the properties of this function and its relation to another equally important function equals (). This information is in all Java textbooks and I do not see the point of repeating it here. I would like to dwell on only one property: the hashCode should be evenly distributed over the function value areas. I thought: “And what is guaranteed by the uniform distribution?”
Looking ahead, I will say that I have come to some rather interesting conclusions. I would like to be corrected if I am mistaken somewhere in the reasoning.
At first, I decided to refer to the Java documentation on Object.hashCode (). As everyone can see, there is no information that interests us. After that I went to the Guru. Bruce Ekkel wrote 5 pages, nodded at Bloch (more precisely, wrote off from him), gave an example with strings, and at the end advised using “useful libraries”. Joshua Bloch did better: he proposed an algorithm for computing, spoke about the benefits of primes and ... also gave an example. I can not help but quit:
')
None of the authors did not bother to analyze the above algorithm and prove its correctness.
1) Take a number other than zero, for example 17. For convenience, we call it p. Assign the result variable is the initial value (result = p).
2) For each field, calculate hashCode c according to some rules. These rules, we are not very interested, they do not affect the result. For simplicity, we will work with integers (int) and will take hashCode equal to the very value of the number ...
3) Combine the result and the resulting hashCode with: result = result * q + c, where q = 37, because, as we remember, it is odd and simple.
4) Return the result.
First, we make several assumptions:
1) As mentioned above, we will work with integers.
2) We assume that hashCode takes values from 0 to 2 32 . That is, we will not work with negative values.
3) We assume that overflow during multiplication and addition does not occur. We will use only small initial values.
4) We will assume that the data on the basis of which hashCode is built are distributed evenly.
To be more specific, I will consider points with integer coordinates (x, y) on a plane in two-dimensional space, provided that x> = 0, y> = 0.
We write the hash function for the point P1 (x1, y1):
h is the hash value of the function.
Now I want to consider some other point P2 (x2, y2) which has the same hash function. That is, it is just a collision case:
Subtract from the first expression the second:
We put out q to the right side:
If we choose such values x1, x2, y1, y2 that the obtained equality is fulfilled, then these coordinates will correspond to the values of the hash argument of the function at which a collision occurs.
You can offer this option:
That is, the points P (38, 1) and P (1, 2) have the same hashCode ... I thought that having 4 billion possible values for the hash code, it would be possible to avoid collisions at least in a 100x100 square!
Now consider the case of n variables, independently varying from 0 to some M. We would like to find the maximum value of M, such that a well-written function hashCode would not have collisions on the interval from 0 to M for all n variables. After some deliberation, we get the value for M:
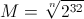
For the case of points on the plane, M takes the value 65536.
It seems that the formula given by Bloch will give an acceptable distribution of hash codes for the case of 8 or more variables.
Now consider points in three-dimensional space. We write a small program that iterates through the points from 0 to 100 (only a million points) and counts the number of collisions. The code of this program is elementary, so I will not give it here. An interesting result: I got 901692 collisions! That is a little more than 90%. It turns out that Bloch, under the guise of the hash function, suggested a function for obtaining collisions?
Now we will try to build a good algorithm for the case of two variables (x1, y1). To uniformly scatter the values of x1 and y1 on the number plane, we use the multiplication: multiply x1 by some number p, and y1 by q. For now, we will not impose any conditions on p and q. To get the value of the hash function, we add these works:
We use the technique described above: we find x2, y2, such that the value of the hash function will produce a collision.
We subtract from the first equality the second:
If q is taken equal to 37 and p is 1, then we obtain a formula from Bloch.
From the last formula and from the fact that we work with integers, it follows:
1) The difference (x1-x2) is proportional to q, the difference (y2-y1) is proportional to p.
2) The greater the p and q, the greater can be the distance between the points.
3) p and q must be mutually simple.
4) Having the upper limit on h = 2 32 , we find that each of the products p * x1, q * y1 must be less than 2 32/2 . It follows that p and q must be less than 32768. For example, 32765 and 32767. Here it should be recalled about our assumption: we work only with positive numbers. When the overflow occurs during the addition, we will find ourselves in the negative part of the numerical axis. I suggest readers think about it yourself.
As Donald Knut wrote in the chapter on the pseudo-random sequence generator, if the algorithm looks complicated and confusing, this does not mean that it works correctly (non-word-writing).
Those who use the implementation of hash functions from Joshua Bloch, but have a large number of hash variables, can sleep well. Also, those who have different types of Hash collections are not a bottleneck in performance.
If you are fighting for the performance of your code, taking into account all the possible trivialities, then you probably should take a fresh look at your hashCode () implementations. Given that the hash values may not be evenly distributed for your specific business area, you can write a hash function with a better distribution of hash codes than any generated option. By rewriting hashCode (), you should probably look at equals (): maybe you can return fewer checks to false.
Thanks to those who read to the end.
Literature:
Bruce Eckel “Thinking in Java Third Edition”
Joshua Bloch “Effective Java: Programming Language Guide”
I will not enumerate here all the properties of this function and its relation to another equally important function equals (). This information is in all Java textbooks and I do not see the point of repeating it here. I would like to dwell on only one property: the hashCode should be evenly distributed over the function value areas. I thought: “And what is guaranteed by the uniform distribution?”
Looking ahead, I will say that I have come to some rather interesting conclusions. I would like to be corrected if I am mistaken somewhere in the reasoning.
Ask Guru
At first, I decided to refer to the Java documentation on Object.hashCode (). As everyone can see, there is no information that interests us. After that I went to the Guru. Bruce Ekkel wrote 5 pages, nodded at Bloch (more precisely, wrote off from him), gave an example with strings, and at the end advised using “useful libraries”. Joshua Bloch did better: he proposed an algorithm for computing, spoke about the benefits of primes and ... also gave an example. I can not help but quit:
The multiplier 37 was chosen. ... it’s clear that it’s not a clear idea.
')
None of the authors did not bother to analyze the above algorithm and prove its correctness.
Algorithm (in free retelling)
1) Take a number other than zero, for example 17. For convenience, we call it p. Assign the result variable is the initial value (result = p).
2) For each field, calculate hashCode c according to some rules. These rules, we are not very interested, they do not affect the result. For simplicity, we will work with integers (int) and will take hashCode equal to the very value of the number ...
3) Combine the result and the resulting hashCode with: result = result * q + c, where q = 37, because, as we remember, it is odd and simple.
4) Return the result.
Algorithm analysis
First, we make several assumptions:
1) As mentioned above, we will work with integers.
2) We assume that hashCode takes values from 0 to 2 32 . That is, we will not work with negative values.
3) We assume that overflow during multiplication and addition does not occur. We will use only small initial values.
4) We will assume that the data on the basis of which hashCode is built are distributed evenly.
To be more specific, I will consider points with integer coordinates (x, y) on a plane in two-dimensional space, provided that x> = 0, y> = 0.
We write the hash function for the point P1 (x1, y1):
(p * q + x1) * q + y1 = h
h is the hash value of the function.
Now I want to consider some other point P2 (x2, y2) which has the same hash function. That is, it is just a collision case:
(p * q + x2) * q + y2 = h
Subtract from the first expression the second:
q (x1-x2) + y1 - y2 = 0 (Note that the multiplier containing p is missing after subtraction)
We put out q to the right side:
(x1 - x2) / (y2-y1) = q (it is clear that the denominator must be different from zero)
If we choose such values x1, x2, y1, y2 that the obtained equality is fulfilled, then these coordinates will correspond to the values of the hash argument of the function at which a collision occurs.
You can offer this option:
x1 = 38
x2 = 1
y2 = 2
y1 = 1
That is, the points P (38, 1) and P (1, 2) have the same hashCode ... I thought that having 4 billion possible values for the hash code, it would be possible to avoid collisions at least in a 100x100 square!
Now consider the case of n variables, independently varying from 0 to some M. We would like to find the maximum value of M, such that a well-written function hashCode would not have collisions on the interval from 0 to M for all n variables. After some deliberation, we get the value for M:
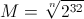
For the case of points on the plane, M takes the value 65536.
It seems that the formula given by Bloch will give an acceptable distribution of hash codes for the case of 8 or more variables.
Now consider points in three-dimensional space. We write a small program that iterates through the points from 0 to 100 (only a million points) and counts the number of collisions. The code of this program is elementary, so I will not give it here. An interesting result: I got 901692 collisions! That is a little more than 90%. It turns out that Bloch, under the guise of the hash function, suggested a function for obtaining collisions?
Good hashCode for two variables
Now we will try to build a good algorithm for the case of two variables (x1, y1). To uniformly scatter the values of x1 and y1 on the number plane, we use the multiplication: multiply x1 by some number p, and y1 by q. For now, we will not impose any conditions on p and q. To get the value of the hash function, we add these works:
p * x1 + q * y1 = h
We use the technique described above: we find x2, y2, such that the value of the hash function will produce a collision.
p * x2 + q * y2 = h
We subtract from the first equality the second:
p * (x1-x2) + q (y1-y2) = 0
or
(x1-x2) / (y2-y1) = q / p (provided that the denominator is non-zero)
If q is taken equal to 37 and p is 1, then we obtain a formula from Bloch.
From the last formula and from the fact that we work with integers, it follows:
1) The difference (x1-x2) is proportional to q, the difference (y2-y1) is proportional to p.
2) The greater the p and q, the greater can be the distance between the points.
3) p and q must be mutually simple.
4) Having the upper limit on h = 2 32 , we find that each of the products p * x1, q * y1 must be less than 2 32/2 . It follows that p and q must be less than 32768. For example, 32765 and 32767. Here it should be recalled about our assumption: we work only with positive numbers. When the overflow occurs during the addition, we will find ourselves in the negative part of the numerical axis. I suggest readers think about it yourself.
findings
As Donald Knut wrote in the chapter on the pseudo-random sequence generator, if the algorithm looks complicated and confusing, this does not mean that it works correctly (non-word-writing).
Those who use the implementation of hash functions from Joshua Bloch, but have a large number of hash variables, can sleep well. Also, those who have different types of Hash collections are not a bottleneck in performance.
If you are fighting for the performance of your code, taking into account all the possible trivialities, then you probably should take a fresh look at your hashCode () implementations. Given that the hash values may not be evenly distributed for your specific business area, you can write a hash function with a better distribution of hash codes than any generated option. By rewriting hashCode (), you should probably look at equals (): maybe you can return fewer checks to false.
Thanks to those who read to the end.
Literature:
Bruce Eckel “Thinking in Java Third Edition”
Joshua Bloch “Effective Java: Programming Language Guide”
Source: https://habr.com/ru/post/169733/
All Articles