Multi-armed bandits: model dynamic Gamma-Poisson
Last time we looked at the general formulation of the multi-armed gang problem, discussed why this might be necessary, and led to a very simple but effective algorithm. Today I will talk about another model that is effective in situations where the expected revenues from gangsters change over time, and the number and composition of the “pens” can change - about the dynamic gamma-Poisson model.
This model refers to the so-called online models of recommendations . Setting a task here is different from offline models (which include the main methods of collaborative filtering - the method of nearest neighbors, SVD and their variants, etc.) in that the main goal of online recommendations is to “catch” changes in the popularity of certain products as soon as possible. . Since, as a rule, there is not enough data so that such changes can be tracked by collaborative filtering methods, online methods usually combine data on the ratings of all users, without engaging in personalized recommendations. Moreover, there are often situations when the system cannot provide reasonable recommendations on the method of collaborative filtering (new user, user who has insufficient nearest neighbors, etc.); in such situations, recommender systems also often issue recommendations based on their online components (see also the recent post by Vasily Leksin on the cold start task - we will continue that series too). As a good overview of the various methods of online recommendations, I can recommend this presentation ; however, these are slides, not text, and everything is very briefly stated there, so it is better to use it as a source of keywords and links.
')
And for the purposes of this post, we will imagine such a situation (I already mentioned it in the previous series). Let us be a portal, make money by placing ads, and as enticing content, we need to post news announcements that users will want to follow (and see even more tasty ads). Below is a typical image showing the (normalized) click-through ratio (CTR) of several news on the Yahoo home page; it can be seen that the changes occur fairly quickly, and these changes are significant: the news quickly “rotten”, and it is impossible to react to this by recounting the collaborative filtering system once a day.
(real news sample from Yahoo home page )
Formally speaking, we have a set of products / sites; we now want to evaluate the CTR of each of them separately, independently, therefore in the future we will work with one of them. We fix the time period t (small) and we will count the impressions (total number of experiments) and clicks (marks like or other desired outcomes) during time t . Suppose we have shown the site n t times during the period t and obtained the rating r t ( r t is an integer less than n t ). Then we are given a sequence at each time t
, and we want to predict p t + 1 , the share of successful impressions (CTR) at time t + 1 .
Here are the first natural ideas:
To solve this problem, it is proposed to use the so-called dynamic Gamma – Poisson model (dynamic gamma-Poisson model, DGP). The probabilistic assumptions of DGP are:
After a lot of mathematical torment (which I will omit here), a very simple iterative algorithm is obtained for recalculating the parameters of this model (in fact, the specific form of the distributions was chosen just to get it: the gamma distribution is a conjugate a priori distribution for the Poisson distribution). Suppose that at the previous step t-1 we obtained a certain estimate μ t , σ t for the parameters of the model:
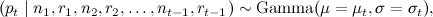
and then received a new point (measurements for the new period of time) n t , r t . Denote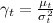
(effective sample size). Then we first refine the estimates μ t , σ t :
and then generate a new prediction for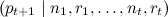
:
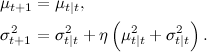
As a result, we will maintain a pair of numbers for each product (each handle).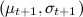
which will change after each time period. A list of top products can be generated simply by ordering them by 
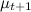(but 
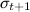it is impossible to forget all the same - the variance is needed to recalculate the average later The approximate behavior of this model on a piece of data from the Yahoo! home page. shown in the figure below - it looks good.
(part of a news sample with predictions of the DGP model)
Further improvement of this model is due to choosing good prior distributions (good μ 0 and σ 0 ) for new pens - this is very important, because new products (for example, fresh news) need to be quickly put into operation, and firstly data about them not much (the very cold start). A good estimate of the a priori distribution is obtained from the negative binomial distribution - suppose that we have in the database N historical records ( N other sites) for which the indicators are known
and 
(the number of impressions and successful impressions for the first period of time); we want to get the estimate μ 0 and σ 0 for a new, unknown site, which should approximate well the expected r 1 and n 1 for the new site. Again, I omit the math, and the answer is - it should be considered as
Where
- gamma function. It is possible to maximize with a gradient lift - from a point we move towards the gradient, i.e. vectors of private derivatives.
Uff. This installation turned out to be noticeably more “mathematical” than the previous one. However, if you do not understand the probabilistic inference that occurred above, do not despair - the output, as before, is a simple algorithm that is very easy to implement and that has a sufficiently clear probabilistic rationale (reasonable assumptions in the model). It can be used in all situations of “gangster” tasks, where you need to quickly respond to changes. For example, in the same example with A / B testing, which I cited last time , it may well be that the behavior or needs of users change over time, and I want to adjust what you are testing to the current situation. And for us in Surfingbird, the DGP model is an important model for displaying pages whose popularity can quickly change with time (the same “news” category, for example); so we quickly understand when the trend of popularity begins to fade.
Next time we will probably talk about some completely different topic; in addition, stay tuned for a cold start cycle in recommender systems. To new texts!
This model refers to the so-called online models of recommendations . Setting a task here is different from offline models (which include the main methods of collaborative filtering - the method of nearest neighbors, SVD and their variants, etc.) in that the main goal of online recommendations is to “catch” changes in the popularity of certain products as soon as possible. . Since, as a rule, there is not enough data so that such changes can be tracked by collaborative filtering methods, online methods usually combine data on the ratings of all users, without engaging in personalized recommendations. Moreover, there are often situations when the system cannot provide reasonable recommendations on the method of collaborative filtering (new user, user who has insufficient nearest neighbors, etc.); in such situations, recommender systems also often issue recommendations based on their online components (see also the recent post by Vasily Leksin on the cold start task - we will continue that series too). As a good overview of the various methods of online recommendations, I can recommend this presentation ; however, these are slides, not text, and everything is very briefly stated there, so it is better to use it as a source of keywords and links.
')
And for the purposes of this post, we will imagine such a situation (I already mentioned it in the previous series). Let us be a portal, make money by placing ads, and as enticing content, we need to post news announcements that users will want to follow (and see even more tasty ads). Below is a typical image showing the (normalized) click-through ratio (CTR) of several news on the Yahoo home page; it can be seen that the changes occur fairly quickly, and these changes are significant: the news quickly “rotten”, and it is impossible to react to this by recounting the collaborative filtering system once a day.
(real news sample from Yahoo home page )
Formally speaking, we have a set of products / sites; we now want to evaluate the CTR of each of them separately, independently, therefore in the future we will work with one of them. We fix the time period t (small) and we will count the impressions (total number of experiments) and clicks (marks like or other desired outcomes) during time t . Suppose we have shown the site n t times during the period t and obtained the rating r t ( r t is an integer less than n t ). Then we are given a sequence at each time t
, and we want to predict p t + 1 , the share of successful impressions (CTR) at time t + 1 .Here are the first natural ideas:
- sort by current
; this sorting will really respond quickly, but most likely will react too quickly, i.e. will be extremely unstable: random fluctuations will have a disproportionately strong effect; - sort by total average
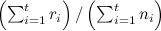; such an approach will have reverse problems - it will very slowly react to changes, and the “rotten” news that has long been left in the top; - sort by the average calculated by the sliding window
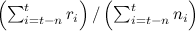; this is quite a reasonable heuristic, but here we do not get estimates for the variance p t + 1 , and also cannot adjust to the different rate of change in different “pens”.
To solve this problem, it is proposed to use the so-called dynamic Gamma – Poisson model (dynamic gamma-Poisson model, DGP). The probabilistic assumptions of DGP are:
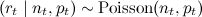(for fixed n t and p t, we get r t distributed over the Poisson distribution);
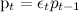where 
(average success rate p t
changes not too fast, but by multiplying by a random variable ε t , which has a gamma distribution around the unit);- Model parameters are distribution parameters.
,
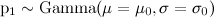as well as the parameter η, which shows how “smoothly” p t can change; accordingly, the task is to evaluate the parameters of the posterior distribution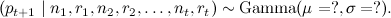
After a lot of mathematical torment (which I will omit here), a very simple iterative algorithm is obtained for recalculating the parameters of this model (in fact, the specific form of the distributions was chosen just to get it: the gamma distribution is a conjugate a priori distribution for the Poisson distribution). Suppose that at the previous step t-1 we obtained a certain estimate μ t , σ t for the parameters of the model:
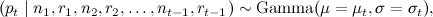
and then received a new point (measurements for the new period of time) n t , r t . Denote
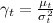(effective sample size). Then we first refine the estimates μ t , σ t :and then generate a new prediction for
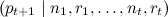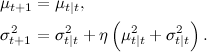
:As a result, we will maintain a pair of numbers for each product (each handle).
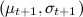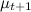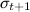which will change after each time period. A list of top products can be generated simply by ordering them by (but it is impossible to forget all the same - the variance is needed to recalculate the average later The approximate behavior of this model on a piece of data from the Yahoo! home page. shown in the figure below - it looks good.(part of a news sample with predictions of the DGP model)
Further improvement of this model is due to choosing good prior distributions (good μ 0 and σ 0 ) for new pens - this is very important, because new products (for example, fresh news) need to be quickly put into operation, and firstly data about them not much (the very cold start). A good estimate of the a priori distribution is obtained from the negative binomial distribution - suppose that we have in the database N historical records ( N other sites) for which the indicators are known
and (the number of impressions and successful impressions for the first period of time); we want to get the estimate μ 0 and σ 0 for a new, unknown site, which should approximate well the expected r 1 and n 1 for the new site. Again, I omit the math, and the answer is - it should be considered asWhere
- gamma function. It is possible to maximize with a gradient lift - from a point we move towards the gradient, i.e. vectors of private derivatives.Uff. This installation turned out to be noticeably more “mathematical” than the previous one. However, if you do not understand the probabilistic inference that occurred above, do not despair - the output, as before, is a simple algorithm that is very easy to implement and that has a sufficiently clear probabilistic rationale (reasonable assumptions in the model). It can be used in all situations of “gangster” tasks, where you need to quickly respond to changes. For example, in the same example with A / B testing, which I cited last time , it may well be that the behavior or needs of users change over time, and I want to adjust what you are testing to the current situation. And for us in Surfingbird, the DGP model is an important model for displaying pages whose popularity can quickly change with time (the same “news” category, for example); so we quickly understand when the trend of popularity begins to fade.
Next time we will probably talk about some completely different topic; in addition, stay tuned for a cold start cycle in recommender systems. To new texts!
Source: https://habr.com/ru/post/169573/
All Articles