Creating a virtual wave

As everyone knows, 71% of the Earth’s surface is water. Unfortunately or fortunately, units are able to correctly depict the ocean. Ivan Aivazovsky entered painting books thanks to seascapes alone. In computer games it is still more difficult. Once upon a time, the sea in them was designated as a cluster of blue pixels painted with white squares of foam. Over time, the virtual seas have become more like pictures of the holidays, learned to swing a wave and become covered in ripples, which sometimes even reflected the outlines of sailing ships. But they remained an independent element: bumping into the shore, the wave turned into plain angular polygons. This surf logically interacts with the beach, moisturizes the sand and rolls back with a rustling sound. This likelihood was achieved only in modern games. Including in our Skyforge. And although the main events will unfold on land, players will get to tropical islands and noisy ports. Water will be constantly near. Her “right” look will play a big role. And the re-creation of the sea element is a serious mathematical task. I'll tell you about the stages of its implementation.

Engine features
')
The graphics engine [a module of a game or other graphics software that is responsible for rendering] Skyforge uses deferred shading technology (see Figure 1): this means that the scene is rendered in two stages. First, there is an intermediate recording in the so-called G-buffer: the specular emission (a) and albedo (b) components of the material of the object are recorded in separate textures, the depth buffer [buffer, in which instead of color the depth value for each point of the scene is recorded] (c) and normals (g). Then, for each light source, the illumination of the final scene is calculated using information from G-buffer (e).





Picture 1.

Deferred shading allows you to illuminate the scene with a much larger number of light sources than with traditional visualization in one pass. However, the approach has limitations: for example, it does not allow to correctly visualize a semi-transparent geometry. In such cases, usually all non-transparent objects are visualized in the first pass using deferred shading (aka deferred pass), and the rest in the second pass using the standard lighting algorithm (aka forward pass).

In Skyforge, water is visualized between deferred and forward pass (d). On the one hand, this allows you to get the necessary information about the depth and light, necessary, for example, to calculate the refraction and reflection from water. On the other hand, effects that require the correct value in the depth buffer (for example, soft particles) interact correctly with water.

A little about the geometry of the water and lighting models

As a geometric model, we use a polygonal mesh [a method of representing three-dimensional objects, in which a surface consisting of polygons (triangles) is used to approximate a surface] with non-uniform detail. Figure 2 shows a polygonal grid of water (a) and the corresponding visualization result (b). The grid detail increases inversely with the distance from the water point to the camera. Waves (deep and surf) are modeled by the displacement of the grid vertices along the vertical axis.

Figure 2.

After calculating the surface of the water is its lighting. We use the lighting model, which takes into account the following factors (Fig. 3):
• reflection of light from the water surface (a);
• a glare from an analytical light source (b);
• foam (in);
• subsurface scattering of light (g);
• light absorption by depth (d);
• refraction of light in the water column (e);
• caustics [light spots formed on one surface due to refraction or reflection from another surface] from the light source at the bottom (g).








Figure 3 .

Surf simulation

Simplistically, the surf is the waves rolling on the shore. In order to create waves moving in a certain direction, we used the equation of a traveling wave:



where A (z, t) is the wave amplitude, k is the wavenumber, φ is the phase, z is the coordinate along which the wave runs. An example of such a wave (with a constant amplitude) is shown in Figure 4. With time and phase, everything is more or less clear, but how to make these waves run to the coast at each point?



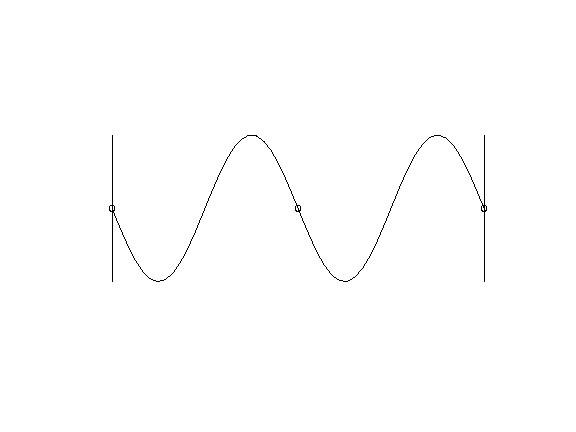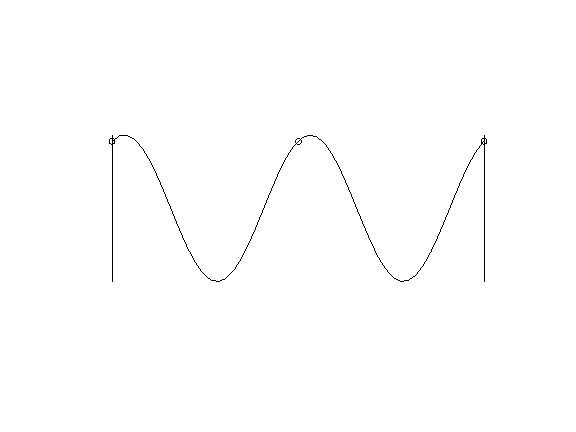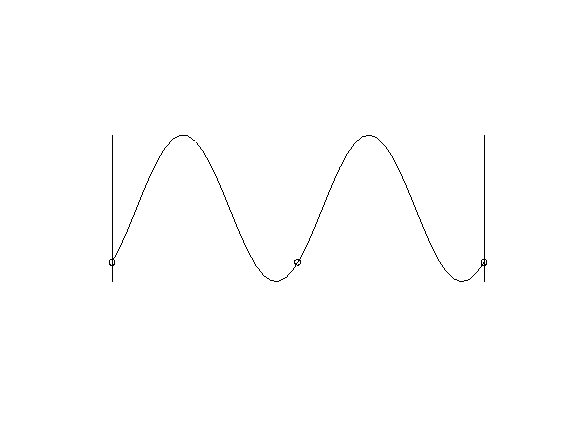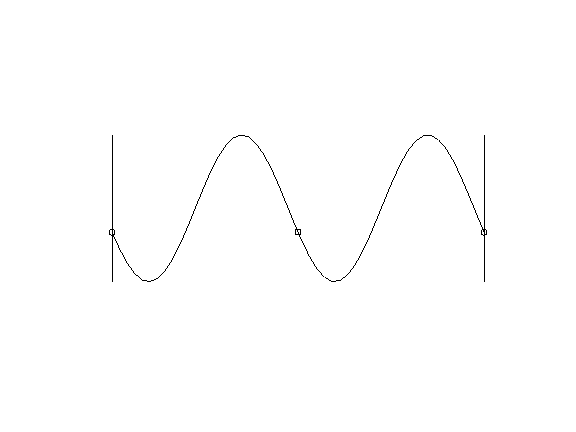
Figure 4.

To do this, we set the z value from the distance field. The distance field is a scalar field whose value at each point is equal to the distance to a given “obstacle”. In our case, the “obstacle” is a landscape that is above sea level. We calculate the distance field in advance and load the map into the texture when loading the map.

If we try our method in action, the result will be completely different from reality (Fig. 5a). The problem is that the waves everywhere go in the same continuous front: the parameter z changes only from the coast, therefore on the isolines of the distance field the wave height h (z, t) will be the same. We solved this problem by creating a mask (5b), which is multiplied by the amplitude of the waves:



where x, y are the coordinates, μ is a coefficient determining the length of the wave segments, ϑ is the rate of appearance / disappearance of waves in a given front.

This mask smoothly changes in time so that the distribution of the waves is uniform. A second wave front is also generated, differing from the first only by the choice of phase φ '. In addition, the waves smoothly appear at depth and smoothly disappear, reaching the coast - this is achieved by choosing the function A (z, t).

Thus, we have obtained a formula by which at any point of the ocean we can find out the amplitude of the wave incident on the shore (5c). This allows you to perform the entire calculation of the surf wave geometry in the vertex shader [program running on the graphics accelerator for each vertex of the polygon mesh of the object] GPU.



Figure 5 .

Waveform

Real waves are not sinusoidal. When approaching the coast, the waves become more and more asymmetrical: a lamb gathers in front, and a gentle train pulls up behind. Finally, the upper part of the wave begins to hang over the lower, the wave breaks and splashes out onto the shore.

We achieve the effect of asymmetry and overhanging of the upper part above the lower one by displacing the wave tops towards the coast in a horizontal plane: the higher the top above the water surface, the more it shifts. You can find the direction vector to the coast by taking the gradient from the distance field. In Figure 6, the dotted line shows such a transformation applied to a sine wave.



Figure 6 .

Gradients are computed in advance and are written to the distance field texture to reduce the number of samples from the texture in the vertex shader.
Foam

Another integral part of the surf is foam. It appears on the crest of the waves and when the waves roll onto the shore. After the wave broke on the shore, the foam rolls back to meet the next wave.

To create these effects, we had to use different techniques. Imitations of movement to the coast and from it are simulated by scrolling texture coordinates [position in the texture, from where you need to take the value for a given vertex / pixel] along the vector of the gradient of the distance field (and, respectively, in the opposite direction). However, if at each point the texture coordinates are constantly shifted, texture pulls are formed due to the unevenness of such shifts. We solve this problem in the following way: two antiphase textures are scrolled, with each sample interpolation occurs. As soon as one of the texture shifts more than a period, it is reset - while its interpolation coefficient is 0, so it goes unnoticed.

Foam on the wave is also distributed asymmetrically. There is no foam in front of the wave, it is very bright on the crest of the wave, and behind it there is a smoothly fading plume behind. To do this, we use the following formula for foam intensity (remember to bring the argument to the correct range):



All parameters, except the phase, coincide with the parameters of the wave. Phase can be slightly shifted to achieve the desired effect.

Behind the oncoming wave the foam runs forward. In our case, it is rather difficult to simulate the geometric wave rollback: the traveling wave equation and the grid topology will be violated. We simulate this effect by imposing near the shore in front of the oncoming wave a foam scrolling towards the wave.
Wet surfaces

Without the effect of wet sand on the shore, the water looks unnatural, separate from the landscape. When wet the sand darkens and begins to shine.

Solution to the forehead: manually tint the coastal zones with darker sand. However, this solution has drawbacks: there will be no glare on this sand, the resolution of the painting will be low, additional work of level designers will be required.







Figure 7 .

We implement this as follows. Near the shore, the surface of the water rises slightly above the level of the landscape, as if creating a “thin film” above (see Fig. 7). Then, when calculating the refraction, the actual color of the landscape is slightly shaded, and a highlight is superimposed on top. Figure 8 shows the effect of the wet sand effect on the final picture.



Figure 8 .

Thank you for attention. I spoke about the intricacies of creating the water element only in general terms. In fact, there are a thousand details and trivia. Together they create an excellent water element. I can say honestly, I am proud of our surf. It is easy to check. Peer at the screenshot.


Sea of ​​solutions

1. How do circles from a floating person diverge? Does foam happen? To understand this, we need references - examples from life. We watched for hours on YouTube videos in which children are splashing at the shore or some guys climb on each other’s shoulders and jump into the water with a bomb. Every month we were asked to send us on an expedition to the sea - of course, only to gather facts! The authorities laughed, but ignored the requests.

2. We wanted the waves to flow naturally on the shore. But the shore can be of any shape. In the north of the huge island, the waves will come from the north, to the south - from the south ... How to take all this into account? We calculated for each point of the ocean a distance field - the distance and vector to the nearest point of the coast. A wave runs along it.

3. Foam - an integral part of the surf. It appears on the crest of the waves and when the waves roll onto the shore. After the wave broke on the shore, the foam rolls back to meet the next wave. To create a convincing foam, I had to suffer a lot - using techniques like scrolling texture coordinates along the gradient field vector of distances, solving the problem of texture pulling and creating other black magic.

4. When wet, the sand darkens and begins to shine. Without this effect, the surf looks unnatural. At first we wanted to tint the coastal areas manually with darker sand, but, firstly, it complicated the work of designers, and secondly, there is no glare on this sand. They came to an elegant solution: on the shore, the water creates a thin film, shading the real color of the landscape, and a sunshine is superimposed on top.

Literature

[1] E. Darles, B. Crespin, D. Ghazanfarpour, JC Gonzato. A Survey of Ocean Simulation and Rendering Techniques in Computer Graphics. Link

[2] Tiago Sousa. Crysis Next Gen Effects. GDC 2008. Link

[3] Carlos Gonzalez-Ochoa. Water Technology of Uncharted. GDC 2012.

[4] Brano Kemen. Ocean Rendering in Outerra. Link

[5] Mike Seymour. Assassin's Creed III: The ech behind (or beneath) the action. Link

Thanks
I would like to thank the Skyforge team, without which this article would not exist, and, in particular, Alexey Kuleshov, Vladimir Egorov, Sergey Makeev, Victor Surkov and Sergey Nazarov.

Peter Sikachev,

Skyforge graphic programmer.

You can find the original article and other useful information on the Skyforge developers website.