Formula white mane horses: perlin noise in pictures

Surely anyone who met with "perlin noise" ( perlin noise ), tried to generate the texture of the clouds.

Because it suggests itself.



On the noise of Perlin on Habré was already an article , but it has very few pictures.

')





In short, the essence of pearly noise is as follows: uniformly distributed random points are connected by a smooth gradient.

It looks not particularly attractive:



However, if you take only the upper half of the waves, do it twice, at 4, and at 8, and put it all together, you will get very recognizable clouds:

+ + + =

Almost the same, but 8 times:





By the squiggle in the center, it is clear that such a construction is fractal, and inevitably has a vanishing point (fixed point). Neighboring squiggles, too, hinted at her. In practice, this does not particularly interfere, or you can shove it somewhere far away.



Here is how the formation of clouds in the texture space:





A reasonable question arises - why are the levels scaled exactly in two times?

Here is an example of an 8-tier cloud with different scaling coefficients:



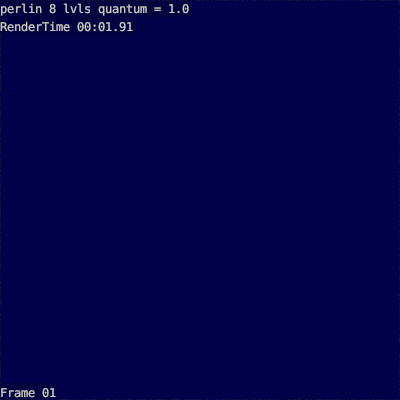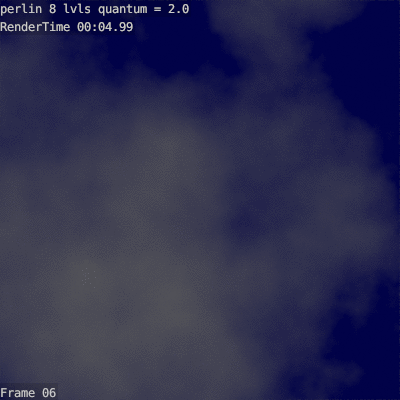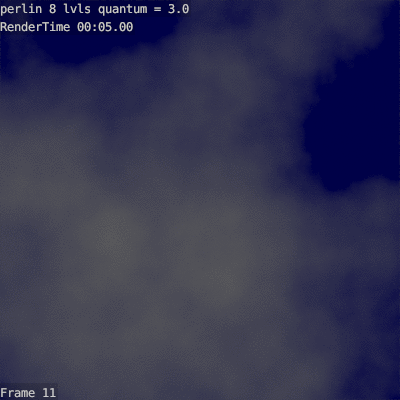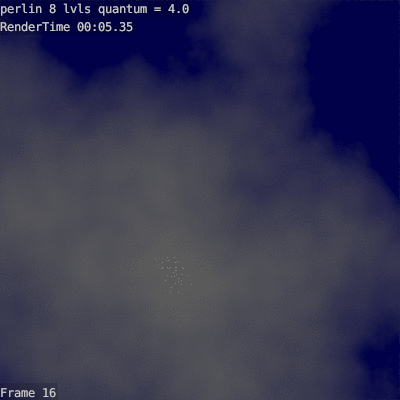
It can be seen that before 1.6 the cloud is not curly enough, and after 2.6 the cloud is too pimply.



You can try to substitute magic numbers:





The golden ratio is a little more blurred, the number e is a bit more crowded.

No miracle happened. Although sometimes with numbers it happens.

Two.



So, the cool cloud formula is:

float acc = 0.0; float amp = 1.0; int i; for(i=0; i<layers; i++){ float v = noise("perlin", scale*pnt); acc += v * amp; amp *= .5; scale *= 2.0; } // max(acc) = (2^n - 1) / 2^n acc *= (float)(1<<(layers)) / (float)((1<<(layers)-1)); return acc * 0.5 + 0.5; } 

Here pnt is a point in the texture space for which the cloud factor is calculated. For example, UV.

The noise function (method, coords) generates the perlin noise value for a given point, in the range from -1 to +1.

There are, for sure, in any graphic library, as well as in the above mentioned habrastiat.



Armed with this formula, you can generate this texture in 3d, and pull it onto a sphere (without bothering with spherical projections, but simply substituting the coordinates of a point of a sphere in space):





You can also generate a four-dimensional texture, and, shifting in time, get live clouds:





For greater persuasiveness, the texture 3d coordinate can still be rotated 30 degrees along the equator, proportional to the square of the cosine of latitude:



Why 30 degrees and the cosine square - I do not know, but this is how real clouds look on the planet.



In fact, real clouds on planet Earth, according to NASA (http://visibleearth.nasa.gov/), look like this:



And the resulting texture has little to do with them.



First, the clouds need to be pulled out.

For decoupling, for each point it is necessary to shift the texture coordinate in some direction, moreover, so that at nearby points the displacement differs slightly. The easiest way to calculate the offset is to use the pearl noise again.

  if(Distortion != 0.0) { point sp = scale[0] * pnt.p; float st = scale[1] * pnt.t; pnt.p[0] += Distortion * noise("perlin", sp + vector(1,0,0), st); pnt.p[1] += Distortion * noise("perlin", sp + vector(0,1,0), st); pnt.p[2] += Distortion * noise("perlin", sp + vector(0,0,1), st); pnt.t += Distortion * noise("perlin", sp, st + 1); } 

Here float scale [2] - scales in space and time, pnt - struct {point p; float t; } coordinates 4d-points.

If you try to save on calls to the function of noise, you will get all sorts of obscenities such as this:



And you need to get a continuously distorted texture in space and time:





Secondly, on the planet the clouds are spread quite torn, and near look like purebred Perlon noise (with scales from 8 to 16 from the size of the planet).



The best I’ve come up with in a week is to multiply the clouds.

Large clouds, meaning mega-air currents, multiplied by small, sheep - as a result, the cloud clouds, distributed along the mega-streams.

∗ =



This is much more like the truth.



Real clouds have varying degrees of graininess, but it’s already too lazy to bother with it.

There was an idea to make another very large cloud and its value to use as a scale parameter for small ones.

This focus did not work - at the boundaries of the scale, wing clouds are indecently shrinking.

In addition, when the planet rotates, the clouds at the equator slow down (this gives a 30 degree twist), but how to do it so that the texture does not twist into the trash, and evaporate smoothly - I did not think of it.

It is probably necessary to use 5d texture, and to displace the twist in the 5th dimension, but bledner and open shading language on which it was coded, 5d do not support. Such a shame ...



However, against the background of the present planet such clouds look quite decent:



Although rendered 1.5 times longer.



An animated comparison of nasa vs perlin is uploaded to youtube .

All the pictures, including the highs of “lewdness” are in the pico-album .

Well, blender-file with all the constructions and scripts on OSL.