Building AI for the game of Japanese Shogi Chess
Not so long ago, I already wrote a small post about the development of AI for the game in the so-called. mini-shogi , but the survey showed that the full-featured post about development will be interesting for the Habras community. Who cares, I ask under the cat.
Building programs that are capable of playing intellectual games is a very interesting task that has great practical and scientific value.
The first attempts to create machines for playing intellectual games (primarily chess) appeared long before the advent of computers. Around 1769, the famous mechanical turkish chess apparatus appeared. The car played quite well, but its whole secret lay in the strong chess player hidden inside.
In the 20th century, mechanical machines gave up their positions to digital computers. A pioneer in this area (as in many others) can be called the famous mathematician Alan Turing. By modern standards, the algorithm he developed was very primitive, and due to the lack of access to real computers, the algorithm had to be executed manually.
')
At about the same time, Claude Shannon proved that there was a better move for any position. He even proposed an algorithm for finding such a move for any game on the final board. Unfortunately, despite the existence of an optimal algorithm, its practical implementation is impossible due to the limited hardware and time resources.
Since the days of Shannon, the task of programming intellectual games has moved from the field of entertainment to the field of serious research. In recent years, on the basis of Shannon's research, practical algorithms have been built, with the help of which computers have learned to play checkers unmistakably and have achieved outstanding success in chess and go.
Shogi Japanese Chess is one of the few games where a person is still stronger than a computer. First of all, this is due to the possibility of returning the taken pieces to the game, this rule dramatically increases the number of possible moves, and therefore makes it difficult to analyze the game. If in chess you can make about 40 moves from an arbitrary position, then in Shogi the number of possible moves is measured in hundreds.
Rules of the game
Before talking about building algorithms for playing shogi, it is necessary to describe the rules of this game.
Figures
In shogi there are 8 different figures (if you take into account the inverted figures, then 14). The rules of moves for various figures are presented in the table:

If you analyze the table, you can make the following observations:
These observations allow to break all the figures into four groups:
Initial arrangement and sequence of the course
Shogi is played by two players, who are called sente (walking first) and gote (walking second), on a square board of 9x9 cells. The initial placement of figures is shown in the picture:

Also, each player has a special stand (komday), where the figures taken from the opponent are placed. It is also accepted to say that the figures taken are “in hand”.
Coups
The last three lines (relative to each player) are the zone of the coup. Any non-inverted piece (except gold and a king) that starts or ends its turn inside this zone can turn over and turn into another piece. The transformation rules are fixed and are shown in the table:

It is important to note that the player makes the decision whether to turn the figure or not. Cases where a coup is necessary are described in the section prohibited moves.
Discharges
The reset rule is what makes the game of shogi one of the most difficult games invented by mankind. The essence of the rule is that any figure eaten from the enemy can be put on any free field as your own.
There are several limitations to the reset rule, but they are quite simple:
Prohibited moves
If the opponent has made a forbidden move, he is immediately counted as a defeat, therefore it is extremely important to know the list of forbidden moves:
The situation of leaving the king in check is not completely clear. If the player does not notice the check to his king, then the opponent may (but is not obliged) to eat the king by the next move. In this case, the game is considered finished.
Game completion
The game ends when one of the players checkmated or made a forbidden move. But in Shogi, there are additional rules for ending the game:
The above rules make a draw result extremely rare for shogi (no more than 3% of all games played). But nevertheless, a draw is possible in one case: if both kings entered the camp of the enemy and fortified there. If both players agree that the situation is a dead end, then points are calculated. All pieces (including in the hand) except for the king, bishop and rook are scored at 1 point, bishop and rook at 5 points, the king is not involved in the calculation.
In professional games, a player who has less than 24 points loses, if both players have at least 24 points, then a draw is declared. In amateur games, the one with at least 27 points wins, if both players have 27 points each, then the victory is awarded to Gote.
Algorithm for finding the best move
MiniMax Algorithm
For the first time, the strategy of finding the best move for any given position was described by Claude Shannon. If you think a little, you can see that this strategy is quite simple and applicable to any game.
Suppose we have some position in which we need to make the best move. First you need to generate all the moves allowed by the rules. Then each of the correct moves must be evaluated. The moves leading to victory will be evaluated as +1, leading to defeat, as -1, and moves leading to a draw position will receive a score of 0.
In order to determine to which outcome the move in question will lead us, we must assume that the enemy will respond to our every move in the best way possible. Those. actually uses the algorithm under consideration: it generates all of its correct moves and chooses the best among them, and to assess how good its course is, it will assume that we will respond in the best way possible, etc.
It turns out that in the procedure for finding the best move on our part, the procedure for finding the best response from the enemy, from which the procedure for finding our best answer to the opponent’s response, etc.
The search function for the best move will recursively call itself until a dull or drawn situation occurs.
At the same time, the assessment of the final position is not difficult, and when evaluating the parent nodes, use the following rules:
This algorithm is called MiniMax. If you graphically depict the call chain, you get a so-called. game tree:

Each node in this tree represents a single analyzed move. The node rating will be equal to the maximum rating of its child nodes. Below is the order in which the nodes will be analyzed (green - win, red - defeat, yellow - draw):
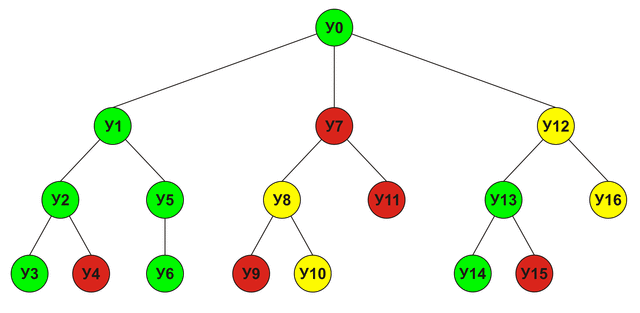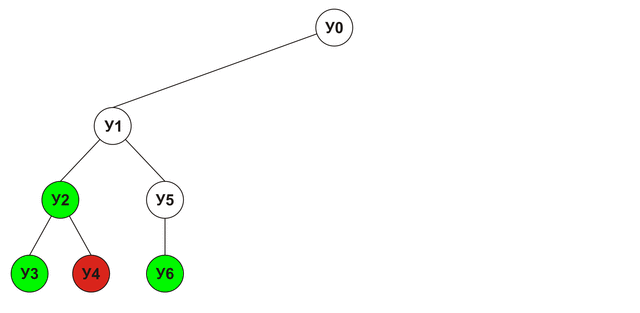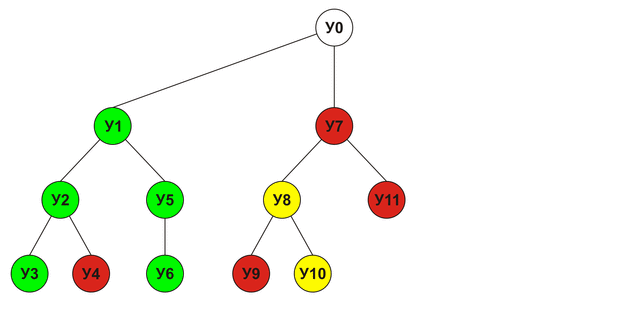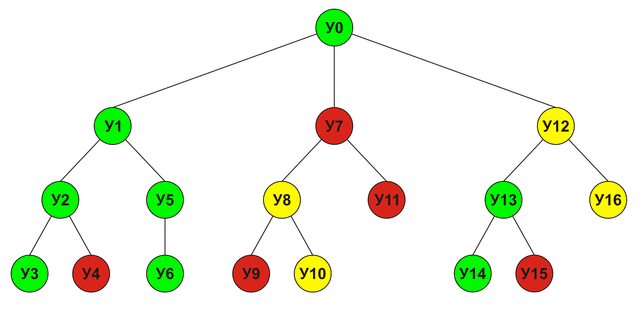
Alpha-Beta clipping
In the example above, to obtain a final assessment of the node U0, we had to get estimates for all the remaining nodes U1-U16, but in fact this was not necessary: as soon as we learned that the node U1 leads to victory, the need to analyze the nodes U7- Y16 disappears, because any estimates obtained for those nodes will not exceed the estimate of node U1 (because it is maximal), which means that there is simply no progress better than U1. Given this, the analyzed tree will look like this:

Obviously, such an abbreviated analysis does not impair the accuracy of the solution, but significantly reduces the search time for a better move. It is the idea of "trimming" unpromising branches of the tree that underlies the Alpha-Beta clipping algorithm.
When using clipping, two variables are additionally introduced: the minimum for sente (A) and the maximum for gote (B). Alpha-Beta's clipping algorithm itself is similar to the MiniMax algorithm, except for the following points:
1. If the evaluation of a move is outside the [A, B] range, then branch analysis can be stopped early, since players have moves leading to a better position.
An important point when using this algorithm is the order of viewing moves. If we first consider those moves that most narrowly limit the range [A, B], then the number of cut branches will be quite large. Returning to the tree discussed above, it is easy to see that the viewing order of the Y7, Y12, and U1 will give a much smaller performance gain. Therefore, before using the algorithms with cut-offs, they pre-sort the moves according to the expected efficiency.
Of course, it is impossible to know in advance which course will be the best, but there are some heuristic rules. For example, good moves are captures, checks, moves that improve position, etc.
Position evaluation function
All the algorithms described above produce viewing the game tree to the full depth, but it is almost impossible to implement such algorithms in practice, so the viewing depth is artificially limited: recursive calls are stopped not only in cases of mate and draws, but also when the maximum depth of analysis is reached. Mats when viewing a tree at a limited depth are relatively rare, and all nematomatic positions have to be assigned a certain heuristic estimate, for which they use the methods described below.
Material evaluation
In most chess-like games, a very accurate assessment of the position is the evaluation of the material. In this case, each piece is assigned a certain value, and the position is estimated for the player as the difference between the sum of his pieces and the sum of the opponent’s pieces. In Shogi, the material estimate is also used, the table of the value of the figures is given below:

All the pieces in the hand are estimated at 30% more expensive, because their mobility due to the possibility of discharge increases significantly.
The high cost of the king and the tokin requires some explanation. Such a high cost of the king is explained by the fact that the king is a figure of absolute importance, with his loss the game ends, therefore the king is valued more than all the other pieces combined. And the cost of a tokin is so high, because a tokin is the best figure for exchanges: in an exchange of tokin silver, one player gets a silver general in his hand, and the second player turns out to be just a pawn.
Strategic assessment
Before talking about the importance of strategic evaluation, it is necessary to note once again the fact that the pieces never leave the game and all taken pieces can return at any time. This fact radically changes the approach to assessing the position.
Firstly, the heuristics of exchanges extremely effective in chess-like games becomes not only ineffective, but also harmful. If you win one pawn in chess and constantly make equal exchanges, then in the endgame one pawn advantage is often decisive. In Shogi, such exchanges can lead to the discharge of enemy figures into your camp.
Secondly, sacrifices are very popular in shogi. For example, at the end of the game, you often have to give up the senior figure for a golden general or a horse to get a figure in your hand that can be mated or an effective fork is made.
If you look at what these two situations have in common, you can see that the enemy took advantage of the unfortunate position of your pieces. In such cases, it is customary to say that the figures have a “bad shape.” In Shogi, form is often more important than material superiority, so the characteristics of the form must be evaluated when evaluating the position. The pictures below are examples of bad and good forms (the unsecured generals are highlighted in red):

The further development of the idea of "good forms" are fortresses - fortifications for the king, ensuring his safety and protecting him from the shahs. Examples of common fortresses are given in the table:

It is clear that good forms should give some plus to a strategic assessment, and bad forms, respectively, worsen the assessment, but in addition to the form, it is also necessary to take into account the control of the board, the proximity of the generals to their own or enemy king, the presence of locked figures, etc.
Summarizing the above, we must once again note that in the function of assessing the position it is necessary to take into account not only the material component, but also the strategic one.
Selective Renewal Algorithm
Already considered MiniMax and Alpha-Beta cut-off algorithms always find the best move at a given depth, but the problem is that the depth of analysis (8-10 moves) is not sufficient for a strong game. Professionals calculate positions for 12-14 moves, and some positions for more than 20 moves. Such a depth for computers is still unattainable.
Some compromise option is to view only some branches of a tree to a considerable depth, while other branches will be viewed at a reduced depth. This approach is called the selective extension method.
In chess programs usually extend the checkers, pawn moves to the last rank and strong captures. But in Shogi, this approach is ineffective. It was decided to perform a search without a fixed depth, increasing the depth step by step. In this case, all possible moves can theoretically be considered at different depths, so it is necessary to additionally remember the depth to which each turn was considered.
Initially, the depth of view of each move is 0, and the stroke estimate is -INF (i.e. loss). At the first iteration, the position is analyzed at a depth of 1 for all moves, each turn gets its own assessment of efficiency, and its viewing depth is increased by 1. Then all moves are ordered by efficiency, and the best moves are analyzed to a depth of 2. If during the next extension It turned out that the move with the maximum estimate has already been analyzed for the maximum depth, then this move is excluded from further consideration. The deepening process continues until all the moves are scanned to the minimum depth. The figure below shows the approximate order of building the tree when using selective extensions (maximum depth - 4, minimum depth - 2, in the nodes the evaluation position at the current viewing depth is shown):
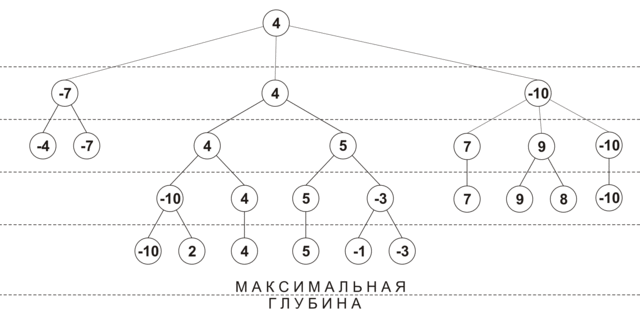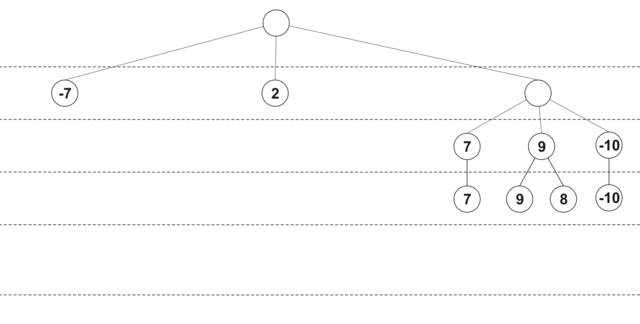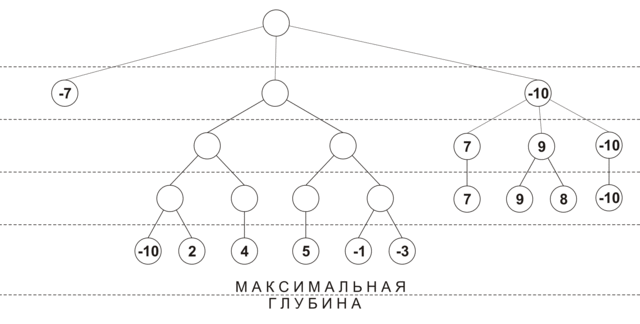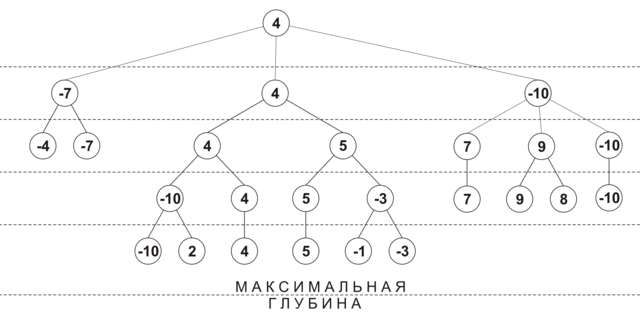
An additional advantage of this algorithm is its effectiveness in games with a time limit: when the time allotted for a move expires, you can return the best of the calculated results.
Caching
It is known that caching is one of the most effective ways to improve program performance. In the context of the construction of game algorithms, caching is used to search for already analyzed positions.
Indeed, during the search for a better move, some positions may be repeated within the same branch or occur in different branches of the tree. The classic algorithm would consider each such position again. Such multiple calculations significantly reduce overall performance. Caching is designed to eliminate the need to perform repeated calculations.
The search for a position in the cache is based on a comparison of the hash functions of the position in question with the hash functions of the positions already in the cache. A feature of most hash functions is the presence of collisions (situations where different input data gives the same value). For games, this behavior of hash functions is unacceptable, since even the slightest change in position greatly affects the optimal course. Given the above, it was decided to use as a hash function a string that uniquely describes the position.
To use caching of results, the following changes must be made to the search algorithm for the best move:
There is another rather subtle point. If the cache already contains the desired position, calculated at a shallow depth, this result can also be used. Recall that the Alpha-Beta clipping algorithm is very sensitive to the order of moves. Practice shows that the assessment obtained with a small depth of miscalculation is a fairly qualitative heuristic assessment of the quality of the course. Those. The values stored in the cache can be used to sort the moves before calling the Alpha-Beta clipping.
The effectiveness of using the cache can be estimated using the following graph, which shows the dependence of the depth of the calculation of the position depending on the time and number of repeated visits.


The graph shows that the use of a cache significantly increases the depth of miscalculation for repetitive positions. For example, with a time limit of 5 seconds per turn, using a cache allows you to achieve the same depth of analysis as a 100-second analysis without using a cache.
So It can be concluded that the use of caching significantly increases the speed of analysis, but it requires a significant amount of memory for storing the processed positions.
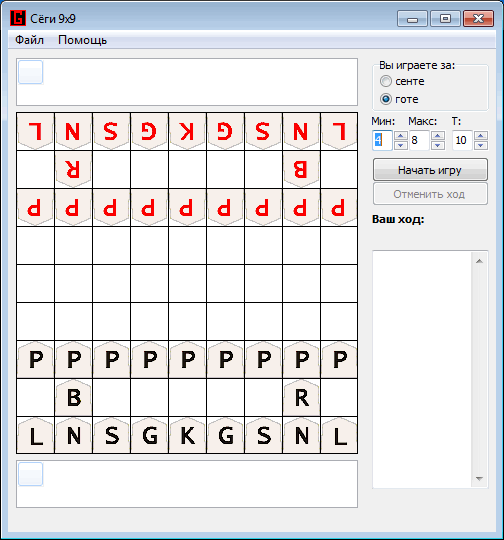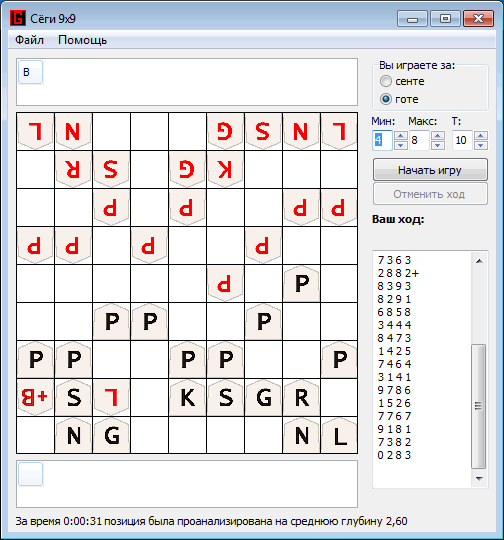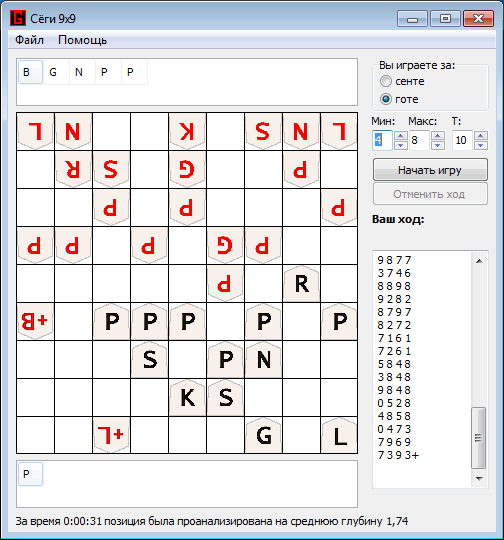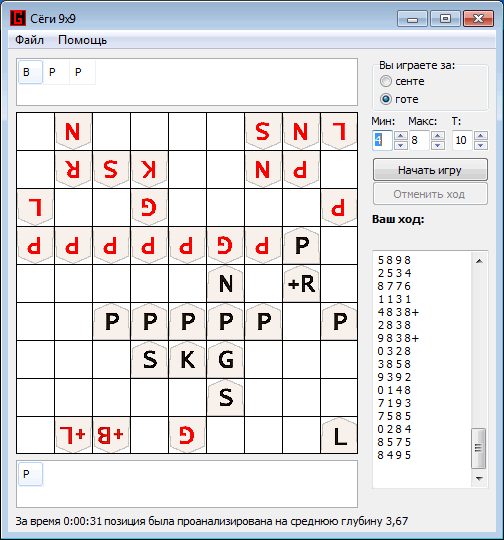
And as a conclusion, a small example of the game developed by the program against the program Shogi Lvl. 100:
Building programs that are capable of playing intellectual games is a very interesting task that has great practical and scientific value.
The first attempts to create machines for playing intellectual games (primarily chess) appeared long before the advent of computers. Around 1769, the famous mechanical turkish chess apparatus appeared. The car played quite well, but its whole secret lay in the strong chess player hidden inside.
In the 20th century, mechanical machines gave up their positions to digital computers. A pioneer in this area (as in many others) can be called the famous mathematician Alan Turing. By modern standards, the algorithm he developed was very primitive, and due to the lack of access to real computers, the algorithm had to be executed manually.
')
At about the same time, Claude Shannon proved that there was a better move for any position. He even proposed an algorithm for finding such a move for any game on the final board. Unfortunately, despite the existence of an optimal algorithm, its practical implementation is impossible due to the limited hardware and time resources.
Since the days of Shannon, the task of programming intellectual games has moved from the field of entertainment to the field of serious research. In recent years, on the basis of Shannon's research, practical algorithms have been built, with the help of which computers have learned to play checkers unmistakably and have achieved outstanding success in chess and go.
Shogi Japanese Chess is one of the few games where a person is still stronger than a computer. First of all, this is due to the possibility of returning the taken pieces to the game, this rule dramatically increases the number of possible moves, and therefore makes it difficult to analyze the game. If in chess you can make about 40 moves from an arbitrary position, then in Shogi the number of possible moves is measured in hundreds.
Rules of the game
Before talking about building algorithms for playing shogi, it is necessary to describe the rules of this game.
Figures
In shogi there are 8 different figures (if you take into account the inverted figures, then 14). The rules of moves for various figures are presented in the table:

If you analyze the table, you can make the following observations:
- There are only two long-range pieces in shogi: the rook and the bishop;
- The possibilities of retreat of many figures are limited or completely absent.
These observations allow to break all the figures into four groups:
- The king of absolute value;
- Senior figures (rook and bishop), capable of long-range attacks and rapid retreat;
- Generals (gold and silver), whose offensive capabilities far exceed the capabilities of retreat;
- Younger pieces (knight, arrow, pawn), not able to retreat.
Initial arrangement and sequence of the course
Shogi is played by two players, who are called sente (walking first) and gote (walking second), on a square board of 9x9 cells. The initial placement of figures is shown in the picture:

Also, each player has a special stand (komday), where the figures taken from the opponent are placed. It is also accepted to say that the figures taken are “in hand”.
Coups
The last three lines (relative to each player) are the zone of the coup. Any non-inverted piece (except gold and a king) that starts or ends its turn inside this zone can turn over and turn into another piece. The transformation rules are fixed and are shown in the table:

It is important to note that the player makes the decision whether to turn the figure or not. Cases where a coup is necessary are described in the section prohibited moves.
Discharges
The reset rule is what makes the game of shogi one of the most difficult games invented by mankind. The essence of the rule is that any figure eaten from the enemy can be put on any free field as your own.
There are several limitations to the reset rule, but they are quite simple:
- All figures are reset not inverted (even if they are dumped into the coup area);
- You cannot drop a pawn to that vertical where there is already a pawn (a tokin is not considered a pawn);
- You can’t fold a pawn with a checkmate.
Prohibited moves
If the opponent has made a forbidden move, he is immediately counted as a defeat, therefore it is extremely important to know the list of forbidden moves:
- Steps that violate the rules (for example, the absence of gold diagonally);
- Violation of the rules of the fold (for example, dropping the second pawn to the vertical);
- A move after which a piece cannot make a single move. This rule requires clarification. You cannot walk a pawn to the last rank without a coup or a knight to the last or next to last rank without a coup. Obviously, it is not possible to reset the figures in this way.
The situation of leaving the king in check is not completely clear. If the player does not notice the check to his king, then the opponent may (but is not obliged) to eat the king by the next move. In this case, the game is considered finished.
Game completion
The game ends when one of the players checkmated or made a forbidden move. But in Shogi, there are additional rules for ending the game:
- If the position is repeated three times as a result of a continuous series of checkers (the so-called “perpetual check”), then for the fourth time the attacking player must make another move, otherwise he will be considered a defeat.
- If the position is repeated 4 times without the announcement of the check, then the players replay the game without the announcement of the results, but with a change of color for the remaining time.
The above rules make a draw result extremely rare for shogi (no more than 3% of all games played). But nevertheless, a draw is possible in one case: if both kings entered the camp of the enemy and fortified there. If both players agree that the situation is a dead end, then points are calculated. All pieces (including in the hand) except for the king, bishop and rook are scored at 1 point, bishop and rook at 5 points, the king is not involved in the calculation.
In professional games, a player who has less than 24 points loses, if both players have at least 24 points, then a draw is declared. In amateur games, the one with at least 27 points wins, if both players have 27 points each, then the victory is awarded to Gote.
Algorithm for finding the best move
MiniMax Algorithm
For the first time, the strategy of finding the best move for any given position was described by Claude Shannon. If you think a little, you can see that this strategy is quite simple and applicable to any game.
Suppose we have some position in which we need to make the best move. First you need to generate all the moves allowed by the rules. Then each of the correct moves must be evaluated. The moves leading to victory will be evaluated as +1, leading to defeat, as -1, and moves leading to a draw position will receive a score of 0.
In order to determine to which outcome the move in question will lead us, we must assume that the enemy will respond to our every move in the best way possible. Those. actually uses the algorithm under consideration: it generates all of its correct moves and chooses the best among them, and to assess how good its course is, it will assume that we will respond in the best way possible, etc.
It turns out that in the procedure for finding the best move on our part, the procedure for finding the best response from the enemy, from which the procedure for finding our best answer to the opponent’s response, etc.
The search function for the best move will recursively call itself until a dull or drawn situation occurs.
At the same time, the assessment of the final position is not difficult, and when evaluating the parent nodes, use the following rules:
- The turn score for the first player is calculated as the maximum of the scores of the child nodes;
- The turn score for the second player is calculated as a minimum of the estimates of the child nodes.
This algorithm is called MiniMax. If you graphically depict the call chain, you get a so-called. game tree:

Each node in this tree represents a single analyzed move. The node rating will be equal to the maximum rating of its child nodes. Below is the order in which the nodes will be analyzed (green - win, red - defeat, yellow - draw):

Alpha-Beta clipping
In the example above, to obtain a final assessment of the node U0, we had to get estimates for all the remaining nodes U1-U16, but in fact this was not necessary: as soon as we learned that the node U1 leads to victory, the need to analyze the nodes U7- Y16 disappears, because any estimates obtained for those nodes will not exceed the estimate of node U1 (because it is maximal), which means that there is simply no progress better than U1. Given this, the analyzed tree will look like this:

Obviously, such an abbreviated analysis does not impair the accuracy of the solution, but significantly reduces the search time for a better move. It is the idea of "trimming" unpromising branches of the tree that underlies the Alpha-Beta clipping algorithm.
When using clipping, two variables are additionally introduced: the minimum for sente (A) and the maximum for gote (B). Alpha-Beta's clipping algorithm itself is similar to the MiniMax algorithm, except for the following points:
1. If the evaluation of a move is outside the [A, B] range, then branch analysis can be stopped early, since players have moves leading to a better position.
- If at any time the first player's score becomes greater than A, then the value of A is updated;
- They do the same with the B score for the second player.
An important point when using this algorithm is the order of viewing moves. If we first consider those moves that most narrowly limit the range [A, B], then the number of cut branches will be quite large. Returning to the tree discussed above, it is easy to see that the viewing order of the Y7, Y12, and U1 will give a much smaller performance gain. Therefore, before using the algorithms with cut-offs, they pre-sort the moves according to the expected efficiency.
Of course, it is impossible to know in advance which course will be the best, but there are some heuristic rules. For example, good moves are captures, checks, moves that improve position, etc.
Position evaluation function
All the algorithms described above produce viewing the game tree to the full depth, but it is almost impossible to implement such algorithms in practice, so the viewing depth is artificially limited: recursive calls are stopped not only in cases of mate and draws, but also when the maximum depth of analysis is reached. Mats when viewing a tree at a limited depth are relatively rare, and all nematomatic positions have to be assigned a certain heuristic estimate, for which they use the methods described below.
Material evaluation
In most chess-like games, a very accurate assessment of the position is the evaluation of the material. In this case, each piece is assigned a certain value, and the position is estimated for the player as the difference between the sum of his pieces and the sum of the opponent’s pieces. In Shogi, the material estimate is also used, the table of the value of the figures is given below:

All the pieces in the hand are estimated at 30% more expensive, because their mobility due to the possibility of discharge increases significantly.
The high cost of the king and the tokin requires some explanation. Such a high cost of the king is explained by the fact that the king is a figure of absolute importance, with his loss the game ends, therefore the king is valued more than all the other pieces combined. And the cost of a tokin is so high, because a tokin is the best figure for exchanges: in an exchange of tokin silver, one player gets a silver general in his hand, and the second player turns out to be just a pawn.
Strategic assessment
Before talking about the importance of strategic evaluation, it is necessary to note once again the fact that the pieces never leave the game and all taken pieces can return at any time. This fact radically changes the approach to assessing the position.
Firstly, the heuristics of exchanges extremely effective in chess-like games becomes not only ineffective, but also harmful. If you win one pawn in chess and constantly make equal exchanges, then in the endgame one pawn advantage is often decisive. In Shogi, such exchanges can lead to the discharge of enemy figures into your camp.
Secondly, sacrifices are very popular in shogi. For example, at the end of the game, you often have to give up the senior figure for a golden general or a horse to get a figure in your hand that can be mated or an effective fork is made.
If you look at what these two situations have in common, you can see that the enemy took advantage of the unfortunate position of your pieces. In such cases, it is customary to say that the figures have a “bad shape.” In Shogi, form is often more important than material superiority, so the characteristics of the form must be evaluated when evaluating the position. The pictures below are examples of bad and good forms (the unsecured generals are highlighted in red):

The further development of the idea of "good forms" are fortresses - fortifications for the king, ensuring his safety and protecting him from the shahs. Examples of common fortresses are given in the table:

It is clear that good forms should give some plus to a strategic assessment, and bad forms, respectively, worsen the assessment, but in addition to the form, it is also necessary to take into account the control of the board, the proximity of the generals to their own or enemy king, the presence of locked figures, etc.
Summarizing the above, we must once again note that in the function of assessing the position it is necessary to take into account not only the material component, but also the strategic one.
Selective Renewal Algorithm
Already considered MiniMax and Alpha-Beta cut-off algorithms always find the best move at a given depth, but the problem is that the depth of analysis (8-10 moves) is not sufficient for a strong game. Professionals calculate positions for 12-14 moves, and some positions for more than 20 moves. Such a depth for computers is still unattainable.
Some compromise option is to view only some branches of a tree to a considerable depth, while other branches will be viewed at a reduced depth. This approach is called the selective extension method.
In chess programs usually extend the checkers, pawn moves to the last rank and strong captures. But in Shogi, this approach is ineffective. It was decided to perform a search without a fixed depth, increasing the depth step by step. In this case, all possible moves can theoretically be considered at different depths, so it is necessary to additionally remember the depth to which each turn was considered.
Initially, the depth of view of each move is 0, and the stroke estimate is -INF (i.e. loss). At the first iteration, the position is analyzed at a depth of 1 for all moves, each turn gets its own assessment of efficiency, and its viewing depth is increased by 1. Then all moves are ordered by efficiency, and the best moves are analyzed to a depth of 2. If during the next extension It turned out that the move with the maximum estimate has already been analyzed for the maximum depth, then this move is excluded from further consideration. The deepening process continues until all the moves are scanned to the minimum depth. The figure below shows the approximate order of building the tree when using selective extensions (maximum depth - 4, minimum depth - 2, in the nodes the evaluation position at the current viewing depth is shown):

An additional advantage of this algorithm is its effectiveness in games with a time limit: when the time allotted for a move expires, you can return the best of the calculated results.
Caching
It is known that caching is one of the most effective ways to improve program performance. In the context of the construction of game algorithms, caching is used to search for already analyzed positions.
Indeed, during the search for a better move, some positions may be repeated within the same branch or occur in different branches of the tree. The classic algorithm would consider each such position again. Such multiple calculations significantly reduce overall performance. Caching is designed to eliminate the need to perform repeated calculations.
The search for a position in the cache is based on a comparison of the hash functions of the position in question with the hash functions of the positions already in the cache. A feature of most hash functions is the presence of collisions (situations where different input data gives the same value). For games, this behavior of hash functions is unacceptable, since even the slightest change in position greatly affects the optimal course. Given the above, it was decided to use as a hash function a string that uniquely describes the position.
To use caching of results, the following changes must be made to the search algorithm for the best move:
- Before starting the calculation, check the availability of the position in the cache;
- If the position is contained in the cache, then stop the calculation and return the value obtained earlier;
- Upon completion of the calculation, write the result to the cache;
There is another rather subtle point. If the cache already contains the desired position, calculated at a shallow depth, this result can also be used. Recall that the Alpha-Beta clipping algorithm is very sensitive to the order of moves. Practice shows that the assessment obtained with a small depth of miscalculation is a fairly qualitative heuristic assessment of the quality of the course. Those. The values stored in the cache can be used to sort the moves before calling the Alpha-Beta clipping.
The effectiveness of using the cache can be estimated using the following graph, which shows the dependence of the depth of the calculation of the position depending on the time and number of repeated visits.


The graph shows that the use of a cache significantly increases the depth of miscalculation for repetitive positions. For example, with a time limit of 5 seconds per turn, using a cache allows you to achieve the same depth of analysis as a 100-second analysis without using a cache.
So It can be concluded that the use of caching significantly increases the speed of analysis, but it requires a significant amount of memory for storing the processed positions.
And as a conclusion, a small example of the game developed by the program against the program Shogi Lvl. 100:

Source: https://habr.com/ru/post/168867/
All Articles