Life on the Lobachevsky plane

Different implementations of the game "Life" have been described on Habré more than once. In this article, as a continuation of this topic, another one of its variants is considered: a regular lattice on the Lobatic plane is used as the playing field. The general methods of using the Lobachevsky plane in programs and the necessary mathematical techniques are described.

It is well known how the Lobachevsky plane originated. In the nineteenth century, Messrs. Gauss, Lobachevsky and Bolyai, who lived around the same time in different countries of Europe at that time, wondered what would happen if the fifth Euclidean postulate was canceled and replaced with the opposite axiom. It turned out that nothing bad would happen, and no contradictions would arise. A notable part of the subsequent study of non-Euclidean geometry was devoted to finding out who among them stole the idea of ​​this geometry.

It is less known that despite the “negative” method of determining non-Euclidean geometry (instead of saying that exactly one straight line passes through a point, we do not intersect a given one, we say that such straight lines can be any number), however, we obtain a system of theorems and formulas that are no less coherent than the one in Euclidean geometry. And at the same time, we have a much greater variety of geometric shapes, including the plane partitions into regular polygons.







So, theorems. The Pythagorean theorem, which sounded like a ² + b ² = c ² , in the geometry of Lobatic takes the form ch (a) ch (b) = ch (c) , the circumference is equal to 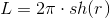and the area of ​​the circle is 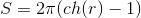. Here sh (x) is the hyperbolic sine, and ch (x) is the hyperbolic cosine. In order to be able to apply mathematical functions to distances with such freedom, we will need some absolute unit of measurement, which is present in Lobachevsky’s geometry (this distance, when shifted by which the distance between “converging” straight lines will decrease exactly e times). The presence of such a unit of distance immediately leads to the fact that the similarity transformation disappears in our country - if we try to change the distances by the same number of times in any figure, the shape of the figure will change. For example, the angle of a regular triangle depends on its side.

But it is possible to build a triangle at three angles (this is done using the second cosine theorem). And it’s quite easy to find the area of ​​a triangle: 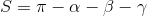. It is seen that the sum of the angles of the triangle is always less 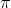, and it can be made as small as desired (the sides of the triangle will tend to infinity, but the area will remain finite).

Choosing the right triangles with angle we get the opportunity to build “parquets” of regular triangles, in which 7.8 converge at one vertex, ... down to infinity of triangles (there is even a variant of “ultra infinity”, but we will not talk about it). In this article we will be interested in parquet {4,5} , which consists of regular quadrangles with angles of 72 ^o . Unfortunately, we are not yet ready to build it.

In addition to our usual lines and circles, there are two more lines on the Lobachevsky plane with similar properties — an equidistant or hypercycle (a set of points at a given distance from a line on the same side of it) and a limit line "or horocycle (a line intersecting a bundle of converging straight lines at a right angle, the limit of a circle with a radius tending to infinity.) Plane movements are of three types - the usual rotation (given by a point and an angle), a shift along a straight line (given by a straight line and an offset) and a shift along the line is a very strange movement, about which it is impossible to say “how much we moved” (in different parts of the plane the magnitude of the shift is different, and all such shifts are in some sense the same). Here it is important that the shift along the straight line is not at all the same thing as parallel translation on the Euclidean plane: different points shift by different distances (points on the shift axis are the least), a straight line can intersect with its image during a shift, etc. In general, the concept of "vector" on the Lobachevsky plane is not, but with the concept of "direction" there are great difficulties.

To work with this plane, we need a coordinate system. Enter it, and even so that it was convenient to work, it is not easy. There is no analogue of Cartesian coordinates (with equal x and y ). You can set a point using the projection on the straight line and the distance to it, but it will not be very convenient. It is better to work in polar coordinates, or take some limit line as an axis (one coordinate is a projection of a point on this line, the other is the distance to it). Fortunately, these coordinate systems allow us to construct very convenient models that Poincare invented.

')

Disc and upper half-plane. Caution, dfcp!

If we take the limit line, we denote by x the projection of a point on it, and by y - the exponent of the distance from the point to the line (taking into account the sign, the distance is

positive from the “concave” side of this line), and consider the points with coordinates (x, y) on the Euclidean plane, we get an amazing fact. The whole Lobachevsky plane will turn into the upper half-plane ( y> 0 ), the lines will turn either into vertical straight lines or into arcs of circles (with centers on the line y = 0 ), the circles will remain circles (with an offset center), and all equidistants and limit lines become straight lines or arcs of circles. Moreover, all angles between straight lines and circles will be preserved.

Such a model is called the Poincaré "half-plane" model . Displacements of the Lobachevsky plane in this model will look like transformations that preserve the straight line y = 0 and translate straight lines and circles into straight lines or circles (Möbius transformations). If instead of points (x, y) we take complex numbers z = x + iy , then such transformations will look like linear fractional functions 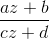and the numbers a, b, c, d must be real. What is good about these transformations is that their composition behaves like matrix multiplication. . This gives us the first hint for the implementation of the Lobachevsky plane: the displacements of the Lobachevsky plane can be represented as 2x2 matrices with real coefficients, defined up to multiplication by a number (i.e. and are considered the same).

Further through M (z) , where 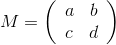Is a 2x2 matrix, and z is a complex number, we will denote the value .

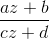Working with matrices and with the upper half-plane is convenient, but not very visual. To visualize the Lobical plane, a transformation is usually applied to this half-plane. 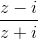, and get a circle of radius 1. Lobachevsky's straight planes are the diameters of this circle and arcs perpendicular to its boundary. This model is called the Poincare disk , we will use it to display the results.

Breaking {4,5}. Careful linear algebra!

For the implementation of the game “Life”, a parquet {4,5} was chosen (splitting the plane into regular 4-squares, 5 cells converge at each vertex). This is one of the two partitions that are most similar to our standard partition {4,4}. The distortion of quadrilaterals in the output will not be very large, and this will allow us to see a larger fragment of the plane at the same time. The second of the mentioned partitions is {5,4} (4 pentagons converge at each vertex), but experiments have shown that this parquet fits a bit less for Life.

To build and use a {4,5} partition, we need to learn how to do a few things. First, find the coordinates of the centers and vertices of the quadrilaterals in our model. Secondly, to somehow number quadrangles in order to distinguish one from another, to find out which are adjacent. And it will also be necessary to learn how to change the center of the picture so that you can explore distant parts of the plane, since all the most interesting things happen, usually, where we are not.

Our usual method of marking cells by pairs of indices does not work here. At all. But we know that each cell is obtained from the central cell by moving the plane, this movement is described by a 2x2 matrix, and the center of the cell will be the image of the center of the central cell, i.e. points (0,1) = i with this displacement. Moreover, the cells adjacent to ours are images of cells adjacent to the central one, while moving. So to create a parquet, we need the following:

• Find the matrix of displacements that translate the central cell to the next;
• Build chains of these movements to find the movements that create the remaining cells;
• To throw out percell, leading to the construction of a cell with an already known center;
• Do not forget that the area of ​​the circle is growing very quickly, so we will have to limit the depth of the search well;
• Find the coordinate of at least one vertex of the central cell. The remaining vertices of it are easy to construct.

Let's start with the fact that we choose a couple of movements from which we can get everything we need. One such move is to rotate R around point i at an angle 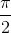(he translates the central cell into himself), and the second - the symmetry T relative to the middle of one side of the central cell - it will translate this cell into the next one. You can check that the matrices of these displacements will be 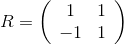and 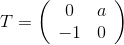where i * a is the center of the neighboring cell (we consider it to be located directly above ours, therefore a> 1 ). To find a , it will be necessary to solve the equation 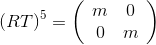for some m ( RT is a rotation around one of the vertices of the cell, and - identical transformation). We do not want to solve the system of equations of the 5th degree, and even analytically (we will need it in the future); therefore, we proceed differently: we say that the eigenvalues ​​of the matrix RT should be the same as the matrix i.e. their characteristic polynomials must match. Omitting the calculations, we get that from where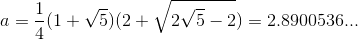



We find the vertex of the quadrilateral by solving the equation RT (z) = z . Here, we do not need an analytical solution, rather a numerical one.

After we built the matrices R and T , and made sure that R ⁴ and (RT) ^{5 are} scalar, building a grid of quadrilaterals is a matter of technique. We take all the matrices M = R ^a TR ^b TR ^c T ... , where a, b, c, ... are numbers from 1 to 3 (perhaps a = 0 ), and we identify those for which M (i ) are the same. Each class of such matrices gives exactly one quadrangle of the lattice. The quadrilaterals corresponding to the matrices M ₁ and M ₂ will be adjacent if M ₂ = M ₁ R ^k TR ^l for some k, l .

For the game on a limited area of ​​the plane this will be enough. It is only necessary to remember that the orientations of the neighboring cells are not initially aligned, therefore, if they are important, then when moving to the next cell, it is necessary to indicate which side (in the orientation of that cell) we came from. It is not easy, but you need to write this piece once :).

To visualize the constructed fragment of the plane, we will need another “camera position” matrix. In our case, this is simply a 2x2 matrix, the same as used to identify cells. If the matrix of the camera F , we want to draw the cell defined by the matrix M , and the coordinate of the point in the coordinate system of this cell is s (a complex number from the “half-plane” model), then to determine where the image of the point is on the Poincaré disk, we find z = F * M (s), w = (zi) / (z + i) . w is the desired point.

Closed areas on the Lobachevsky plane. Careful end fields!

As I said, the area of ​​a circle on the Lobachevsky plane is growing very quickly. An increase in radius of 1 will increase the area approximately threefold. Therefore, if we specify, for example, a million cells, then at best they will cover a circle with a radius of 13. For the game “Life” this is not enough, they like homogeneous areas without borders. So we have a task before us - how to cut a piece from our parquet and glue its edges so that at each vertex 5 quadrangles still converge? The simple method that is used for the Cartesian grid does not work — we do not have any rectangles. But he gives a hint: there, if we cut out from the lattice {4,4} a square with side P , where P is simple, then the cells (x ₁ , y ₁ ) and (x ₂ , y ₂ ) are considered identical if x ₁ = x ₂ (mod P) and y ₁ = y ₂ (mod P) . Why don't we do the same? Each cell we have corresponds to the matrix 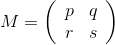, which is a product of matrices R and T , taken in some quantity and order. Two matrices correspond to one cell if M ₂ = M ₁ R ^k . All we need is to choose P such that the matrices R and T modulo P exist.

With matrix 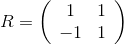everything is simple - it always exists. For T to exist, the expression needs to be 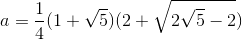it was calculated modulo P (this is why we needed to find it in analytical form). The number of modules P for which such an expression can be calculated is small (approximately every 30th). For example, P = 179 . According to this module, we get 1433790 cells, which is quite normal for the game. Anyway, at a time, we see only a few thousand of them.

After we have chosen the module, we will construct all possible products of R and T modulo P (up to a constant factor) - there will be no more of them than P ³ -P . For each matrix, we will remember the cell to which this matrix corresponds (the matrices M and MR always correspond to the same cell), and for each cell, some matrix. Then for each cell we find the numbers of all its neighbors - separately bordering on the sides, separately - at the corners. And finally, when constructing a geometric model together with the matrix M defining the cell, we will consider its representation modulo P , carefully calculating the product of the matrices R (mod P) and T (mod P) in the same degrees.

All counted, you can start working. We only note that we don’t need a lot of cells in the geometric model - ten thousand is enough. And so that through this model one could look at any part of the playing field, we will do so.

In addition to the matrix F (camera position), we will also store the matrix Q , given modulo P - this will be the “field location under the camera”. In particular, the Q matrix itself will be one of the representations of the cell above which the camera is located. To draw the cell with the number k from the geometric model, we take the matrix M _k (mod P) from this cell, calculate C _k = Q * (M _k (mod P)) , and find the cell from our field corresponding to the matrix C _k ( we once remembered it). And draw the entire contents of the cell, using the matrix FM _k , as indicated in the previous section.

If, when the camera moves, we have gone beyond the central cell, and now the center of the geometric model with the number is drawn in the center 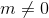, then the projection of the field on the model must be moved. We will say that now we will use F '= FM _m as the camera position, and we will take Q' = Q (M _m (mod P)) as the matrix of the field location. If this does not work (and should work), we will see right away - when moving over the field, the image will not always move continuously.

Actually the game "Life"

In general, nothing interesting left. The main task was navigation in the plane of Lobachevsky, and the game “Life” was just the simplest of its practical application. But since we're here ...

We have a list of fields. To set a state (a cell is alive or dead) is not a problem. The problem is to choose interesting rules. Of course, Conway with his 4th order rules is unrealistic to catch up with, but at least you want to catch gliders.

In order to have more freedom, it was decided to consider the neighbors on the sides and in the corners separately, and for each combination to give their answer "alive or dead." It soon became clear that if the cells came to life with at least 4 neighbors, then we would not see gliders, and it is necessary that at least in the situation “one living neighbor on the side and two in the corners” the cell was born (this rule is written as B12). Good results were given by the rule B12,4 / S2,3,4 (the cell is born in situation 2 in a corner, one side - or with 4 living neighbors in any combination, and remains alive with 2,3,4 living neighbors - again, in any combination). There were many stable figures, several interesting pulsars, and instead of gliders some “shock waves” periodically flew by. Unfortunately, as the initial density increases, the configuration becomes chaotic, and its density stays at 1/3.

Another interesting configuration is B12,21 / S3,4,6 (a cell is born if it has exactly three living neighbors, and there must be living neighbors on the side and in the corner, and it survives if there are 3, 4 or 6 living neighbors). There are few stable figures and pulsars in this world, but there are a lot of gliders. In fact, the entire field consists of gliders and their debris (the density is kept at 1/200), so they do not live long.

Other findings

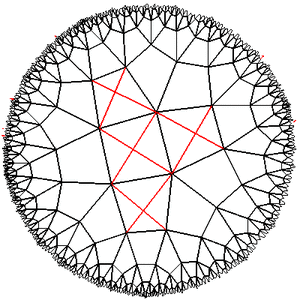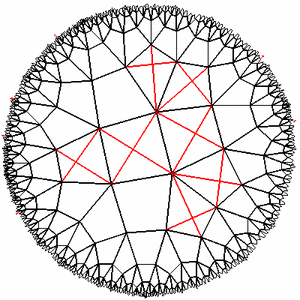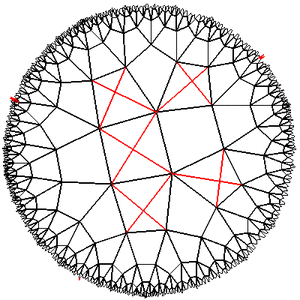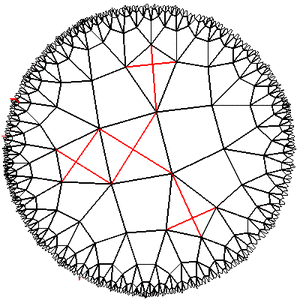Experiments with the Lobachevsky plane showed that it is indeed very small in size and large in area. If you move a few steps away from something, then its apparent size will decrease to complete indistinguishability, and it will be very difficult to come back. If you try to circumvent any obstacle, even the fact that you turn right all the time does not guarantee that your path will close (for example, if we walk along the squares {4,5} and turn 90 grams every two step, then go away infinitely far). Areas that seem to be narrow free gaps between zones filled with living cells can actually be a huge empty space, and the area of ​​living cells, if viewed from afar, will be a small spot on a completely empty horizon ...

In general, the object is interesting. And if someone is bored with flat playing fields, and you don’t want to go into three dimensions, you can try to transfer the game to the lattices of the Lobachevsky plane. Suddenly work?



Airframe span





Walk on the plane of the series "we all die"





Fragment of the game on the grid {5,4}