Parallel programming in Python using multiprocessing and shared array

Introduction

Python is a great language. A bunch of Python + NumPy + Matplotlib, in my opinion, is now one of the best for scientific calculations and fast prototyping algorithms. But each instrument has its own light and dark sides. One of the most discussed features of Python is GIL - Global Interpreter Lock. I would attribute this feature to the dark side of the instrument. Although many will disagree with me.

In short, GIL does not allow more than one stream to be used effectively in a single Python interpreter. GIL advocates claim that single-threaded programs with GIL are much more efficient. But the presence of GIL means that parallel computing using multiple threads and shared memory is not possible. And this is quite a strong limitation in the modern multi-core world.

One of the ways to overcome GIL using threads in C ++ was recently reviewed in the article: Using Python in a multi-threaded C ++ application . I want to consider another way to overcome the limitations of GIL, based on multiprocessing and shared array. In my opinion, this method allows using processes and shared memory for transparent parallel programming in the style of multiple threads and shared memory quite simply and efficiently.

Task.

As an example, consider the following problem. In the three-dimensional space, N points v0, v1, ..., vN are given. It is required for each pair of points to calculate a function depending on the distance between them. The result will be an NxN matrix with the values ​​of this function. As a function, we take the following: f = r ^ 3/12 + r ^ 2 / 6. This test, in fact, is not so synthetic. RBF interpolation, which is used in many areas of computational mathematics, is based on calculating such functions of distance.
')

Parallelization method.

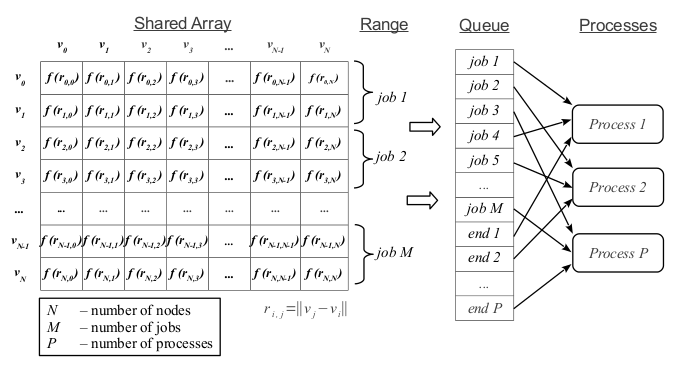
In this problem, each row of the matrix can be calculated independently. For every few rows of the matrix, we will form independent works and place them in the task queue (see fig. 1). Run some processes. Each process will take the next task from the queue for execution until it encounters a special task with the “end” code. In this case, the process ends its work.

Implementation in Python.

In the Python implementation, we will have two main methods: mpCalcDistance (nodes) and
mpCalcDistance_Worker (nodes, queue, arrD). The mpCalcDistance (nodes) method takes as input a list of nodes, creates a shared memory area, prepares a job queue, and starts processes. The mpCalcDistance_Worker method (nodes, queue, arrD) is a computational method that runs in its own thread. It takes as input a list of nodes, a job queue, and a shared memory area. Consider the implementation of these methods in more detail.

Method mpCalcDistance (nodes)

Create a shared memory area:

nP = nodes.shape[0] nQ = nodes.shape[0] arrD = mp.RawArray(ctypes.c_double, nP * nQ) 

Create a job queue. Each task is nothing but a simple range of rows of the matrix. The special value None is a sign of the completion of the process:

  nCPU = 2 nJobs = nCPU * 36 q = nP / nJobs r = nP % nJobs jobs = [] firstRow = 0 for i in range(nJobs): rowsInJob = q if (r > 0): rowsInJob += 1 r -= 1 jobs.append((firstRow, rowsInJob)) firstRow += rowsInJob queue = mp.JoinableQueue() for job in jobs: queue.put(job) for i in range(nCPU): queue.put(None) 

We create processes and wait until the queue of tasks ends:

  workers = [] for i in range(nCPU): worker = mp.Process(target = mpCalcDistance_Worker, args = (nodes, queue, arrD)) workers.append(worker) worker.start() queue.join() 

From the area of ​​shared memory form a matrix with the results:

  D = np.reshape(np.frombuffer(arrD), (nP, nQ)) return D 

Method mpCalcDistance_Worker (nodes, queue, arrD)

Wrap the shared memory area in the matrix:

  nP = nodes.shape[0] nQ = nodes.shape[0] D = np.reshape(np.frombuffer(arrD), (nP, nQ)) 

Until the queue of tasks is over, we take the following task from the queue and perform the calculation:

  while True: job = queue.get() if job == None: break start = job[0] stop = job[0] + job[1] # components of the distance vector p = nodes[start:stop] q = nodes.T Rx = p[:, 0:1] - q[0:1] Ry = p[:, 1:2] - q[1:2] Rz = p[:, 2:3] - q[2:3] # calculate function of the distance L = np.sqrt(Rx * Rx + Ry * Ry + Rz * Rz) D[start:stop, :] = L * L * L / 12 + L * L / 6 queue.task_done() 

results

Runtime: dual-core processor, Ubuntu 12.04, 64bit.


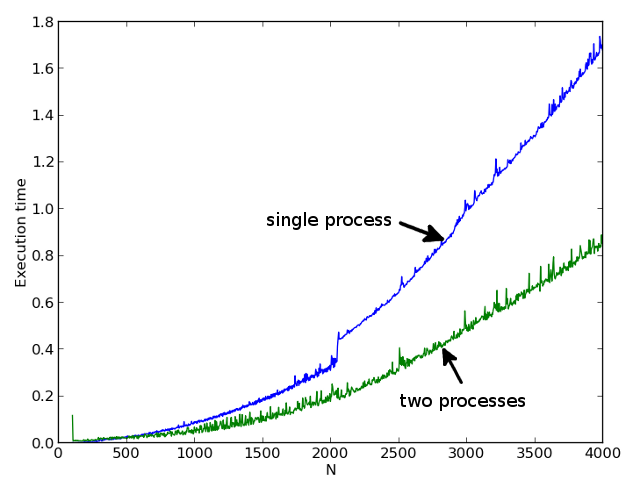
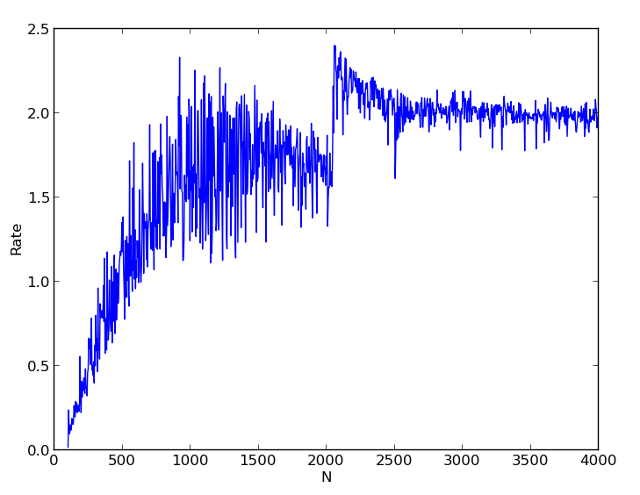
The first picture shows the times of single-stream and two-stream calculations for different N. The second picture shows the ratio of single-stream to double-stream calculations. It can be seen that starting from N = 500, we already receive a significant acceleration of the calculation.

A very interesting result is obtained in the region of the number N = 2000. In the single-threaded version, we get a noticeable jump in the calculation time, and in a multi-threaded calculation, the acceleration factor even exceeds 2. I explain this with the cache effect. In a multi-threaded version, the data for each task is completely cached. And in the one-threaded no longer.

So the use of processes and shared memory, in my opinion, simply allows you to bypass the limitations of GIL.

Full code of the whole script:

 """ Python multiprocessing with shared memory example. This example demonstrate workaround for the GIL problem. Workaround uses processes instead of threads and RawArray allocated from shared memory. See also: [1] http://docs.python.org/2/library/multiprocessing.html [2] http://folk.uio.no/sturlamo/python/multiprocessing-tutorial.pdf [3] http://www.bryceboe.com/2011/01/28/the-python-multiprocessing-queue-and-large-objects/ """ import time import ctypes import multiprocessing as mp import numpy as np import matplotlib.pyplot as plt def generateNodes(N): """ Generate random 3D nodes """ return np.random.rand(N, 3) def spCalcDistance(nodes): """ Single process calculation of the distance function. """ p = nodes q = nodes.T # components of the distance vector Rx = p[:, 0:1] - q[0:1] Ry = p[:, 1:2] - q[1:2] Rz = p[:, 2:3] - q[2:3] # calculate function of the distance L = np.sqrt(Rx * Rx + Ry * Ry + Rz * Rz) D = L * L * L / 12 + L * L / 6 return D def mpCalcDistance_Worker(nodes, queue, arrD): """ Worker process for the multiprocessing calculations """ nP = nodes.shape[0] nQ = nodes.shape[0] D = np.reshape(np.frombuffer(arrD), (nP, nQ)) while True: job = queue.get() if job == None: break start = job[0] stop = job[0] + job[1] # components of the distance vector p = nodes[start:stop] q = nodes.T Rx = p[:, 0:1] - q[0:1] Ry = p[:, 1:2] - q[1:2] Rz = p[:, 2:3] - q[2:3] # calculate function of the distance L = np.sqrt(Rx * Rx + Ry * Ry + Rz * Rz) D[start:stop, :] = L * L * L / 12 + L * L / 6 queue.task_done() queue.task_done() def mpCalcDistance(nodes): """ Multiple processes calculation of the distance function. """ # allocate shared array nP = nodes.shape[0] nQ = nodes.shape[0] arrD = mp.RawArray(ctypes.c_double, nP * nQ) # setup jobs #nCPU = mp.cpu_count() nCPU = 2 nJobs = nCPU * 36 q = nP / nJobs r = nP % nJobs jobs = [] firstRow = 0 for i in range(nJobs): rowsInJob = q if (r > 0): rowsInJob += 1 r -= 1 jobs.append((firstRow, rowsInJob)) firstRow += rowsInJob queue = mp.JoinableQueue() for job in jobs: queue.put(job) for i in range(nCPU): queue.put(None) # run workers workers = [] for i in range(nCPU): worker = mp.Process(target = mpCalcDistance_Worker, args = (nodes, queue, arrD)) workers.append(worker) worker.start() queue.join() # make array from shared memory D = np.reshape(np.frombuffer(arrD), (nP, nQ)) return D def compareTimes(): """ Compare execution time single processing versus multiple processing. """ nodes = generateNodes(3000) t0 = time.time() spD = spCalcDistance(nodes) t1 = time.time() print "single process time: {:.3f} s.".format(t1 - t0) t0 = time.time() mpD = mpCalcDistance(nodes) t1 = time.time() print "multiple processes time: {:.3f} s.".format(t1 - t0) err = np.linalg.norm(mpD - spD) print "calculate error: {:.2e}".format(err) def showTimePlot(): """ Generate execution time plot single processing versus multiple processing. """ N = range(100, 4000, 4) spTimes = [] mpTimes = [] rates = [] for i in N: print i nodes = generateNodes(i) t0 = time.time() spD = spCalcDistance(nodes) t1 = time.time() sp_tt = t1 - t0 spTimes.append(sp_tt) t0 = time.time() mpD = mpCalcDistance(nodes) t1 = time.time() mp_tt = t1 - t0 mpTimes.append(mp_tt) rates.append(sp_tt / mp_tt) plt.figure() plt.plot(N, spTimes) plt.plot(N, mpTimes) plt.xlabel("N") plt.ylabel("Execution time") plt.figure() plt.plot(N, rates) plt.xlabel("N") plt.ylabel("Rate") plt.show() def main(): compareTimes() #showTimePlot() if __name__ == '__main__': main()