The predestination of the development of information waves
Hi habr!
I already wrote about the possibility of predicting the development of information waves and social trends by analyzing the diffusion of innovation for a particular sample. Some time passed, I consulted with the luminaries of media analytics and statistics, acquired new knowledge on the topic and formulated new ideas.
I'll start in order.
')
There is a theory of diffusion of innovation . This is a theory called by its existence to explain how, why, and at what speed new ideas and technologies spread in society. The main essence of the theory, perhaps, can be expressed in one graph.
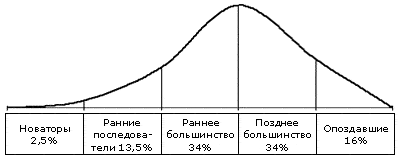
It goes without saying that the percentage on the graph is an average, and depending on the sample and subject matter, it will change along with all the variables. More importantly, the form of the function graph will always be monotonous. This is in principle understandable to anyone and means only that every trend, like all living things on earth, once comes a beginning and sometime ends.
Nicholas Kristakis and James Fowler (Harvard pundits), using the theory of diffusion of innovation and building social graphs, at one point made a startling discovery, a discovery that is most obvious to the point of genius.
Taking a sample of people connected with each other and having determined the unit of information disseminated, they divided the sample in a ratio of 10/90, where group A - 10% of people with the greatest number of social connections within the sample, and group B - all the rest. For each group, for the same topic were the diffusion graphics of innovation.
The result was always the following:

The fact that group A, which has a large number of social connections and is located closer to the center of the social graph, perceives all information waves before group B is obvious, in principle, and without plotting. Much more important that the form of such graphs, of course in the appropriate percentage ratio, will always strive for absolute imitation. This means that by tracking the distribution of information from a certain group of users, we can predict the distribution of such information in a group 10 times longer than the observed one in a quite respectable period (depending on the environment, information and qualities of the network actors ).
It seems to me that this is amazing.
Albert-Laszlo Barabashy - the creator of the theory of scale-free networks . Networks in which the degrees of the vertices are distributed according to a power law. It has been empirically proven that scale-free networks are one of the favorite tools of Mother Nature, because most of the naturally obtained networks (biological, cosmic and, of course, social) are built in this way.

On the left in the figure, a typical network is shown based on randomly compiled data.
It is sensitive to attacks, if several actors are taken out of it at random, then the damage can be great up to complete destruction.
On the right is a scale-free network, a small number of nodes in it are characterized by numerous connections, and many nodes have only a small number of connections, therefore, it is less likely to cause damage to it by accidental removal of actors.
Of course, any social graph will be a scale-free network.
This means that it is possible to single out the most reasonable groups of actors.
This means that, depending on the weight of the actors (the possibilities of disseminating information), they can be grouped together and compared with larger actors (for example, a large group of users with a newspaper).
It means that the actors can be distributed into a whole pyramid of social weight and track the distribution of information at each level.
I do not know about you, but I admire such a method to the very depths of the soul and imagination peaks.
But too happy here can not be. Of course, that the distribution of information is influenced by many third-party factors, which are simply impossible to track through the Internet (and we are talking about it). It is impossible to completely predetermine any informational wave, but there is good news - you can strive for the absolute endlessly, creating for example an infinite number of matrices for specific characteristics of a topic or sample.
We should also raise the ethical question of tracking people's moods.
This suggests a comparison with nuclear power, which can be packaged in bombs and distributed to third-world dictators, or it can be distributed in bulk to everyone.
Thank you for your attention and interest.
I already wrote about the possibility of predicting the development of information waves and social trends by analyzing the diffusion of innovation for a particular sample. Some time passed, I consulted with the luminaries of media analytics and statistics, acquired new knowledge on the topic and formulated new ideas.
I'll start in order.
')
There is a theory of diffusion of innovation . This is a theory called by its existence to explain how, why, and at what speed new ideas and technologies spread in society. The main essence of the theory, perhaps, can be expressed in one graph.

It goes without saying that the percentage on the graph is an average, and depending on the sample and subject matter, it will change along with all the variables. More importantly, the form of the function graph will always be monotonous. This is in principle understandable to anyone and means only that every trend, like all living things on earth, once comes a beginning and sometime ends.
Nicholas Kristakis and James Fowler (Harvard pundits), using the theory of diffusion of innovation and building social graphs, at one point made a startling discovery, a discovery that is most obvious to the point of genius.
Taking a sample of people connected with each other and having determined the unit of information disseminated, they divided the sample in a ratio of 10/90, where group A - 10% of people with the greatest number of social connections within the sample, and group B - all the rest. For each group, for the same topic were the diffusion graphics of innovation.
The result was always the following:

The fact that group A, which has a large number of social connections and is located closer to the center of the social graph, perceives all information waves before group B is obvious, in principle, and without plotting. Much more important that the form of such graphs, of course in the appropriate percentage ratio, will always strive for absolute imitation. This means that by tracking the distribution of information from a certain group of users, we can predict the distribution of such information in a group 10 times longer than the observed one in a quite respectable period (depending on the environment, information and qualities of the network actors ).
It seems to me that this is amazing.
Albert-Laszlo Barabashy - the creator of the theory of scale-free networks . Networks in which the degrees of the vertices are distributed according to a power law. It has been empirically proven that scale-free networks are one of the favorite tools of Mother Nature, because most of the naturally obtained networks (biological, cosmic and, of course, social) are built in this way.

On the left in the figure, a typical network is shown based on randomly compiled data.
It is sensitive to attacks, if several actors are taken out of it at random, then the damage can be great up to complete destruction.
On the right is a scale-free network, a small number of nodes in it are characterized by numerous connections, and many nodes have only a small number of connections, therefore, it is less likely to cause damage to it by accidental removal of actors.
Of course, any social graph will be a scale-free network.
This means that it is possible to single out the most reasonable groups of actors.
This means that, depending on the weight of the actors (the possibilities of disseminating information), they can be grouped together and compared with larger actors (for example, a large group of users with a newspaper).
It means that the actors can be distributed into a whole pyramid of social weight and track the distribution of information at each level.
I do not know about you, but I admire such a method to the very depths of the soul and imagination peaks.
But too happy here can not be. Of course, that the distribution of information is influenced by many third-party factors, which are simply impossible to track through the Internet (and we are talking about it). It is impossible to completely predetermine any informational wave, but there is good news - you can strive for the absolute endlessly, creating for example an infinite number of matrices for specific characteristics of a topic or sample.
We should also raise the ethical question of tracking people's moods.
This suggests a comparison with nuclear power, which can be packaged in bombs and distributed to third-world dictators, or it can be distributed in bulk to everyone.
Thank you for your attention and interest.
Source: https://habr.com/ru/post/167279/
All Articles