Catalana numbers
Undoubtedly, the most remarkable mathematical fact is the identity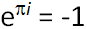 
. It seemed in an amazing way that seemingly completely unconnected constants from different areas of mathematics came together. It is not so difficult to prove this identity, but few manage to explain it, to understand the deep meaning.
As another remarkable fact, I would like to recall the numbers of Catalan, which miraculously emerge in a variety of combinatorial problems. Unfortunately, they fall out of consideration of the typical school curriculum, but I am sure that any computer science specialist should be familiar with them.
The Catalan number itself is expressed by the formula C (n) = (2n)! / N! (N + 1) !, where the exclamation mark, as usual, means factorial. The beginning of the sequence looks like this: 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796 ...
English Wikipedia claims that at least 66 different constructions are known, which lead to the appearance of Catalan numbers. Here are some of them:
For each of these constructions, it is possible either by induction or by recurrent relations to prove that the number of corresponding objects is expressed by the Catalan number. I will not dwell on this evidence - they can be found in textbooks on discrete mathematics. There are also some remarkable ratios that can be obtained using some of the mentioned constructions. But this requires writing cumbersome formulas, which I would like to avoid. What is more interesting now is the coincidence of all these quantities for completely different things?
Of course not. The connection of these structures is much deeper. You can build a one-to-one correspondence between these objects and I will try to demonstrate some of these correspondences. In addition to simple curiosity, it has some practical value. For example, the problem of generating all binary trees (the solution of which in the forehead is not obvious) can be reduced to a much simpler problem of generating bracket sequences.
It is very easy to construct a correspondence between bracket sequences and monotone paths in a square. Reading the bracket sequence from left to right, we will build a path, starting from the lower left corner - for each opening bracket we draw a horizontal segment, for a closing bracket - a vertical segment.
Since the sequence had an equal number of opening and closing brackets, the path will end up in the upper right corner, and the fact that each opening bracket is earlier than the corresponding closing bracket (the sequence is correct) ensures that the path does not go to the upper half of the square. Obviously, this construction is reversible and one can get a bracket sequence from each monotone path.
In the above figure, the corresponding brackets and segments are marked with one color. It is well seen that the segments corresponding to one pair of brackets "see each other":
As the second task, we construct a correspondence between the correct bracket sequences and the tables Young 2xn. Here, too, everything is simple. We number the brackets from left to right. If the bracket opens, then we write the corresponding number in the upper line. If closing, then at the bottom. Since the i-th opening bracket is always to the left of the i-th closing one, the number corresponding to the opening bracket will be less than the number corresponding to the closing one. So, the upper number in the table will be less than the lower one in the same column, that is, from the correct bracket sequence, we get a Young table. This construction is also reversible, and therefore a one-to-one correspondence is obtained.
Now we will deal with binary trees. It is very easy to see the correspondence between binary trees and the arrangement of parentheses in an expression with homogeneous operations, but this gives slightly different sequences. To bind binary trees to the correct bracket sequences, you must use a slightly different approach. We use the standard tree traversal and number the vertices (we take the root as 0) in the traversal order. Now, if during the transition to the number I we descended from parent to child, then we put the opening bracket on the i-th place. Otherwise, we put a closing one.
The tree is binary, so each node has a neighbor. So, going down to the child and putting the opening bracket, we will sooner or later get to his neighbor and put a closing bracket. This ensures that the resulting sequence is correct. The construction is easy to reverse and using the bracket sequence to obtain a binary tree.
Note that if in the bracket sequence n pairs, then the corresponding tree has n + 1 leaves.
To construct a correspondence between the triangulations of a polygon, the simplest way is to use a binary tree. This time we will enumerate all the leaves in it from left to right (the other nodes will be marked with letters). For triangulation, we take a polygon in which there are one more vertices than leaves in a tree. One of the sides of this polygon is noted as the starting one, and the others are numbered (counterclockwise for clarity).
Next, we perform the following procedure - if the two vertices of the tree are adjacent, then the corresponding sides of the polygon are “pulled together” with a diagonal, which we mark with the letter that marks the parent of this pair of nodes in the tree. Next, we continue the “tightening” procedure until a single starting segment remains from the polygon.
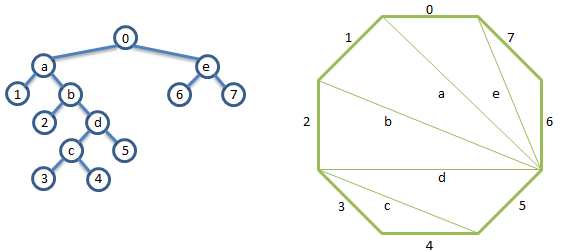
As you can see, the three sides of each triangle in the resulting partition correspond to one parent node and its two descendants. Therefore, if you take two different trees, you get two different partitions.
Well, in conclusion, I will give a sign, which shows the correspondence of objects for the third day of Catalan.
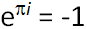. It seemed in an amazing way that seemingly completely unconnected constants from different areas of mathematics came together. It is not so difficult to prove this identity, but few manage to explain it, to understand the deep meaning.As another remarkable fact, I would like to recall the numbers of Catalan, which miraculously emerge in a variety of combinatorial problems. Unfortunately, they fall out of consideration of the typical school curriculum, but I am sure that any computer science specialist should be familiar with them.
The Catalan number itself is expressed by the formula C (n) = (2n)! / N! (N + 1) !, where the exclamation mark, as usual, means factorial. The beginning of the sequence looks like this: 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796 ...
English Wikipedia claims that at least 66 different constructions are known, which lead to the appearance of Catalan numbers. Here are some of them:
- Correct bracket sequences are sets of opening and closing brackets, in which each opening bracket corresponds to a closing one. The number of possible sequences with a fixed number of pairs of brackets is expressed by the number of Catalan. For example, 14 regular sequences of four pairs of brackets:
(((()))), ((() ())), ((()) ()), ((())) (), (() (())) (() () ()), (() ()) (),
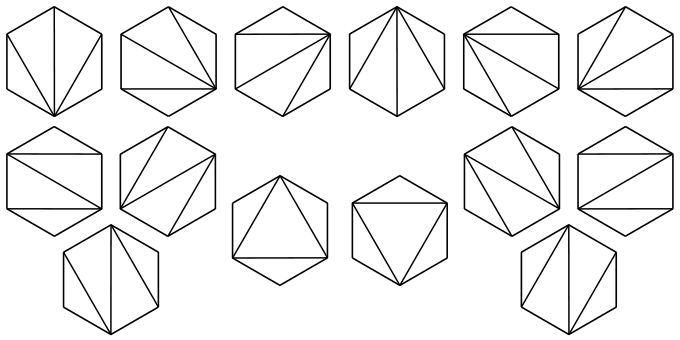
(()) (()), (()) () (), () ((())), () (() ()), () (()) (), () () ( ()), () () () () - Binary trees are trees, from each node of which (except for leaves) exactly two branches come out. The number of binary trees with a given number of leaves is the Catalan number. The figure shows five trees with 4 leaves in each.
Such trees have already been discussed on Habré
') - Any trees. The number of non-isomorphic trees with a given number of vertices is also equal to the number of Catalan. Such trees were also discussed.
- Monotone paths in the square are the routes from the lower left corner of the square to the upper right, which go up or to the right along the grid lines and do not go above the diagonal. In the figure, all such paths are for a 3x3 square.
- Polygon triangulation. The number of different triangulations of a convex polygon by the diagonals is equal to the Catalan number.
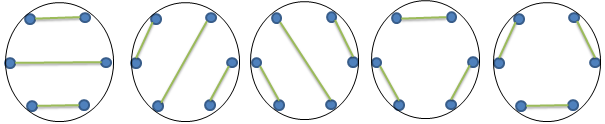
- Splitting vertices of a polygon into pairs. An even number of points on a circle can be combined into pairs with non-intersecting chords. The number of methods of such associations is also equal to the number of Catalan.
- Young table is a rectangle filled with consecutive numbers so that they grow in all rows and columns. The number of Young table sizes of 2xn is also expressed by the Catalan number.
For each of these constructions, it is possible either by induction or by recurrent relations to prove that the number of corresponding objects is expressed by the Catalan number. I will not dwell on this evidence - they can be found in textbooks on discrete mathematics. There are also some remarkable ratios that can be obtained using some of the mentioned constructions. But this requires writing cumbersome formulas, which I would like to avoid. What is more interesting now is the coincidence of all these quantities for completely different things?
Of course not. The connection of these structures is much deeper. You can build a one-to-one correspondence between these objects and I will try to demonstrate some of these correspondences. In addition to simple curiosity, it has some practical value. For example, the problem of generating all binary trees (the solution of which in the forehead is not obvious) can be reduced to a much simpler problem of generating bracket sequences.
Compliance 1
It is very easy to construct a correspondence between bracket sequences and monotone paths in a square. Reading the bracket sequence from left to right, we will build a path, starting from the lower left corner - for each opening bracket we draw a horizontal segment, for a closing bracket - a vertical segment.
Since the sequence had an equal number of opening and closing brackets, the path will end up in the upper right corner, and the fact that each opening bracket is earlier than the corresponding closing bracket (the sequence is correct) ensures that the path does not go to the upper half of the square. Obviously, this construction is reversible and one can get a bracket sequence from each monotone path.
In the above figure, the corresponding brackets and segments are marked with one color. It is well seen that the segments corresponding to one pair of brackets "see each other":
Match 2
As the second task, we construct a correspondence between the correct bracket sequences and the tables Young 2xn. Here, too, everything is simple. We number the brackets from left to right. If the bracket opens, then we write the corresponding number in the upper line. If closing, then at the bottom. Since the i-th opening bracket is always to the left of the i-th closing one, the number corresponding to the opening bracket will be less than the number corresponding to the closing one. So, the upper number in the table will be less than the lower one in the same column, that is, from the correct bracket sequence, we get a Young table. This construction is also reversible, and therefore a one-to-one correspondence is obtained.
Match 3
Now we will deal with binary trees. It is very easy to see the correspondence between binary trees and the arrangement of parentheses in an expression with homogeneous operations, but this gives slightly different sequences. To bind binary trees to the correct bracket sequences, you must use a slightly different approach. We use the standard tree traversal and number the vertices (we take the root as 0) in the traversal order. Now, if during the transition to the number I we descended from parent to child, then we put the opening bracket on the i-th place. Otherwise, we put a closing one.
The tree is binary, so each node has a neighbor. So, going down to the child and putting the opening bracket, we will sooner or later get to his neighbor and put a closing bracket. This ensures that the resulting sequence is correct. The construction is easy to reverse and using the bracket sequence to obtain a binary tree.
Note that if in the bracket sequence n pairs, then the corresponding tree has n + 1 leaves.
Match 4
To construct a correspondence between the triangulations of a polygon, the simplest way is to use a binary tree. This time we will enumerate all the leaves in it from left to right (the other nodes will be marked with letters). For triangulation, we take a polygon in which there are one more vertices than leaves in a tree. One of the sides of this polygon is noted as the starting one, and the others are numbered (counterclockwise for clarity).
Next, we perform the following procedure - if the two vertices of the tree are adjacent, then the corresponding sides of the polygon are “pulled together” with a diagonal, which we mark with the letter that marks the parent of this pair of nodes in the tree. Next, we continue the “tightening” procedure until a single starting segment remains from the polygon.
As you can see, the three sides of each triangle in the resulting partition correspond to one parent node and its two descendants. Therefore, if you take two different trees, you get two different partitions.
Instead of an epilogue
Well, in conclusion, I will give a sign, which shows the correspondence of objects for the third day of Catalan.
Source: https://habr.com/ru/post/165295/
All Articles