The simplest image clustering by the k-means method (k-means)
Often when searching for moving objects in video, whether by subtracting the background, time difference, optical flow, we end up with a lot of points that, after the action of the above algorithms, are marked as having changed their position relative to the previous frame and are related to the foreground.
After such processing, there is a question about the segmentation of objects by the method of cluster analysis, which will be discussed below and its implementation in C ++.
')
First, a little theory:
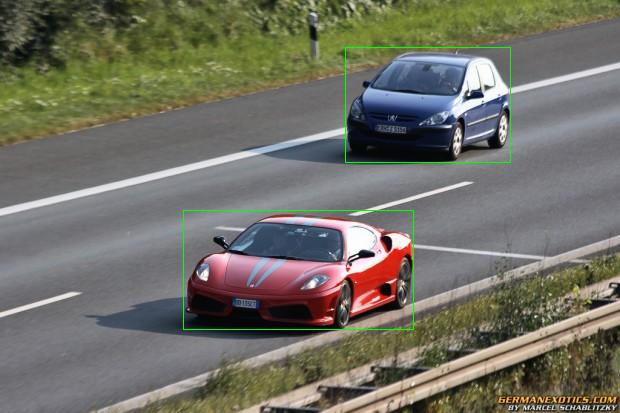
Segmentation is the process of splitting a digital image into multiple segments (sets of pixels). Simply put, this is the thing that allows you to determine which pixels from this set belong to Ferrari, and which to Peugeot.
From the point of view of computing resources, it is very effective to use cluster analysis methods for segmentation. The essence of clustering is that all source objects (in this case, pixels) are divided into several non-intersecting groups so that objects that fall into one group have similar characteristics, while for objects from different groups these characteristics should significantly differ. The resulting groups are called clusters. The initial values in the simplest way for clustering are pixel coordinates (x, y), in more complex cases, for example for half-tone images, a three-dimensional vector (x, y, I (x, y)) is used, where I (x, y) - grayscale
and a five-dimensional vector if RGB is used.
Centroid - the point which is the center of the cluster.
k-means (k-means) is the most popular clustering method. The algorithm is widely preferred because of its ease of implementation, high speed (and this is very important when working with video).
The algorithm is such that it seeks to minimize the total square deviation of cluster points from the centers of these clusters. In common speech, this is an iterative algorithm that divides a given set of pixels into k clusters of points, which are as close as possible to their centers, and the clustering itself occurs due to the displacement of these same centers. Such a principle of divide and conquer.
You should also stipulate that the k-means method is very sensitive to noise, which can significantly distort the results of clustering. So ideally, before clustering, you need to drive frames through filters designed to reduce it.
Here is the very principle of the simplest clustering method K-means:
Here is a picture that roughly demonstrates the operation of the algorithm:

Here is a good applet to illustrate the operation of the k-means algorithm.
First we need a class, let's call it Cluster, which will store the vector of coordinates of pixels belonging to the cluster, the current and previous values of the coordinates of the centroid:
Now we need to implement a method that will distribute the initial coordinates of the centroids. Of course, you can do something more complicated, but in our case, even distribution along the vector will do:
You also need to write a method that will be responsible for finding the centroid coordinates in accordance with paragraph 5. The coordinates of the new centroid can be found by describing a rectangle around the cluster pixels and then the centroid will be the intersection of its diagonals.
And now it only remains to make an unpretentious method of “attaching” pixels to a specific cluster itself on the principle of comparing modules of segments:
Finally, the main loop:
Let us return to the picture with machines, clustering moving objects, a problem arises when using the k-means algorithm, namely, we don’t know how many moving objects there will be in this scene, although we can approximately predict. For example, a frame with machines, on that scene, it would be reasonable to assume that well, there will be a maximum of 10 machines. Thus, setting the program input to k = 10 and outlining the points of 10 clusters with green rectangles, we get something like this:

Now it’s commonplace to intersect intersecting rectangles, we find the resulting clusters, by circling that with a rectangle we will get an image translated at the beginning of the post. Everything is simple.

After such processing, there is a question about the segmentation of objects by the method of cluster analysis, which will be discussed below and its implementation in C ++.
')
Object Segmentation
First, a little theory:
Segmentation is the process of splitting a digital image into multiple segments (sets of pixels). Simply put, this is the thing that allows you to determine which pixels from this set belong to Ferrari, and which to Peugeot.
From the point of view of computing resources, it is very effective to use cluster analysis methods for segmentation. The essence of clustering is that all source objects (in this case, pixels) are divided into several non-intersecting groups so that objects that fall into one group have similar characteristics, while for objects from different groups these characteristics should significantly differ. The resulting groups are called clusters. The initial values in the simplest way for clustering are pixel coordinates (x, y), in more complex cases, for example for half-tone images, a three-dimensional vector (x, y, I (x, y)) is used, where I (x, y) - grayscale
and a five-dimensional vector if RGB is used.
K-medium method
Centroid - the point which is the center of the cluster.
k-means (k-means) is the most popular clustering method. The algorithm is widely preferred because of its ease of implementation, high speed (and this is very important when working with video).
The algorithm is such that it seeks to minimize the total square deviation of cluster points from the centers of these clusters. In common speech, this is an iterative algorithm that divides a given set of pixels into k clusters of points, which are as close as possible to their centers, and the clustering itself occurs due to the displacement of these same centers. Such a principle of divide and conquer.
You should also stipulate that the k-means method is very sensitive to noise, which can significantly distort the results of clustering. So ideally, before clustering, you need to drive frames through filters designed to reduce it.
Here is the very principle of the simplest clustering method K-means:
- It is necessary to choose from the set of k pixels those pixels that will be the centroids of the corresponding k clusters.
A sample of initial centroids can be either randomly or according to a certain algorithm. - We enter a cycle that continues until the centroids of the clusters stop changing their position.
- We go around each pixel and see which centroid of which cluster it is nearby.
- Found a nearby centroid? Bind a pixel to the cluster of this centroid.
- Touched all the pixels? Now you need to calculate the new coordinates of the centroids of k clusters.
- Now check the coordinates of the new centroids. If they are respectively equal to the previous centroids, we exit the cycle, if not, we return to step 3.
Here is a picture that roughly demonstrates the operation of the algorithm:

Here is a good applet to illustrate the operation of the k-means algorithm.
Let's start
First we need a class, let's call it Cluster, which will store the vector of coordinates of pixels belonging to the cluster, the current and previous values of the coordinates of the centroid:
class Cluster{ vector<POINT> scores; public: int curX , curY;// int lastX, lastY;// size_t Size(){ return scores.size();}// inline void Add(POINT pt){ scores.push_back(pt); }// void SetCenter(); void Clear();// static Cluster* Bind(int k, Cluster * clusarr, vector<POINT>& vpt); static void InitialCenter(int k, Cluster * clusarr , vector<POINT>& vpt);; static void Start(int k, Cluster * clusarr, vector<POINT>& vpt); inline POINT& at(unsigned i){ return scores.at(i);}// }; Now we need to implement a method that will distribute the initial coordinates of the centroids. Of course, you can do something more complicated, but in our case, even distribution along the vector will do:
void Cluster::InitialCenter(int k, Cluster * clusarr, vector<POINT>& vpt){ int size = vpt.size(); int step = size/k; int steper = 0; for(int i = 0;i < k;i++,steper+=step){ clusarr[i].curX = vpt[steper].x; clusarr[i].curY = vpt[steper].y; } } You also need to write a method that will be responsible for finding the centroid coordinates in accordance with paragraph 5. The coordinates of the new centroid can be found by describing a rectangle around the cluster pixels and then the centroid will be the intersection of its diagonals.
void Cluster::SetCenter(){ int sumX = 0, sumY = 0; int i = 0; int size = Size(); for(; i<size;sumX+=scores[i].x,i++);//the centers of mass by x i = 0; for(; i<size;sumY+=scores[i].y, i++);//the centers of mass by y lastX = curX; lastY = curY; curX = sumX/size; curY = sumY/size; } void Cluster::Clear(){ scores.clear(); } And now it only remains to make an unpretentious method of “attaching” pixels to a specific cluster itself on the principle of comparing modules of segments:
Cluster * Cluster::Bind(int k, Cluster * clusarr, vector<POINT>& vpt){ for(int j = 0; j < k;j++) clusarr[j].Clear();// int size = vpt.size(); for(int i = 0; i < size; i++){// int min = sqrt( pow((float)clusarr[0].curX-vpt[i].x,2)+pow((float)clusarr[0].curY-vpt[i].y,2) ); Cluster * cl = &clusarr[0]; for(int j = 1; j < k; j++){ int tmp = sqrt( pow((float)clusarr[j].curX-vpt[i].x,2)+pow((float)clusarr[j].curY-vpt[i].y,2) ); if(min > tmp){ min = tmp; cl = &clusarr[j];}// } cl->Add(vpt[i]);// } return clusarr; } Finally, the main loop:
void Cluster::Start(int k, Cluster * clusarr, vector<POINT>& vpt){ Cluster::InitialCenter(k,clusarr,vpt); for(;;){// int chk = 0; Cluster::Bind(k,clusarr,vpt);// for(int j = 0; j < k;j++)// clusarr[j].SetCenter(); for(int p = 0; p<k;p++)// - if(clusarr[p].curX == clusarr[p].lastX && clusarr[p].curY == clusarr[p].lastY) chk++; if(chk == k) return;// } } And what follows from all this?
Let us return to the picture with machines, clustering moving objects, a problem arises when using the k-means algorithm, namely, we don’t know how many moving objects there will be in this scene, although we can approximately predict. For example, a frame with machines, on that scene, it would be reasonable to assume that well, there will be a maximum of 10 machines. Thus, setting the program input to k = 10 and outlining the points of 10 clusters with green rectangles, we get something like this:

Now it’s commonplace to intersect intersecting rectangles, we find the resulting clusters, by circling that with a rectangle we will get an image translated at the beginning of the post. Everything is simple.
Source: https://habr.com/ru/post/165087/
All Articles