Javascript: Draw with Bezier Curves
Good day, habrazhiteli!
I really like the baroque elements. Once again, having met a similar pattern on one of the sites, I imagined how he would look wonderful in animation, the picture would come to life. Especially with the advent of html5, the animation should be much easier to implement. But how on points to draw a curve? Then just by the way I remember the Bezier curve!
In vector graphics lessons, I hated Bezier curves. The principle of its work seemed magical, incomprehensible and, if not to say coarser, illogical. The feeling was that the curve itself did not know how to twist, and how arrogant the tomcat was stretching as it was more convenient for her, and not as I needed.
In fact, as always, it was only necessary to devote a little time to the theory. Everything turned out to be simple and quite interesting. The result was the implementation of the curves in javascript using canvas.
Who cares how to build this winding beast welcome under the cut!
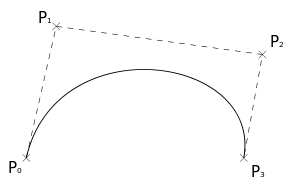
Let's start with the principle of construction. The Bezier curve is constructed on several reference points. Figuratively speaking: the curve starts at the zero reference point, begins to move to the first, but suddenly notices the second - starts to touch it, smoothly changes its route in its direction, and then a third appears on the horizon, even more attractive ... And so passing by points, the curve stops its choice at the last reference point, where it comes. The path turns out like an alcoholic going home in the morning.
')
From the lyrics go to the harsh mathematics.
The theory is brazenly borrowed from Wikipedia :
The Bezier curve is a special case of Bernstein polynomials, is a parametric curve and is given by the expression:
 where
where
n is the number of reference points;
i is the number of the reference point;
t is the step at which we consider the position of the curve. For example, when building a curve using 100 points, the step will be 0.01 (not the reference, but points on the curve itself);
P - in our case, the coordinate of the reference point;
b (t) is the basic function of the Bezier curve. This coefficient determines the weight of the reference point. The Bernstein polynom itself is:

where Is the number of combinations of n through i , where n is the degree of the polynomial, i is the sequence number of the reference vertex.
Is the number of combinations of n through i , where n is the degree of the polynomial, i is the sequence number of the reference vertex.
In the first and last steps, the value of the Bernstein polynomial is 1, the explanation is here . The midpoint of the curve is most influenced by the middle reference points, in the first third - the reference points of the first third, and so on. Bernstein polynom takes values from 0 to 1.
And so, to calculate the coordinate of the Bezier curve, we need:
With the theory sort of figured out, go to the practice.
We consider the basic function:
Next we get the coordinates of the curve.
You can build a Bezier curve in three-dimensional, four-dimensional space, and so on, but we will stop on a plane.
Draw a curve:
It's time to try:
Jsfiddle example
Related Links:
Article on javascript.ru
upd: The HTML5 standard supports quadraticCurveTo and bezierCurveTo methods for building Bezier curves by three and four points, respectively. Thank you lany .
I really like the baroque elements. Once again, having met a similar pattern on one of the sites, I imagined how he would look wonderful in animation, the picture would come to life. Especially with the advent of html5, the animation should be much easier to implement. But how on points to draw a curve? Then just by the way I remember the Bezier curve!
In vector graphics lessons, I hated Bezier curves. The principle of its work seemed magical, incomprehensible and, if not to say coarser, illogical. The feeling was that the curve itself did not know how to twist, and how arrogant the tomcat was stretching as it was more convenient for her, and not as I needed.
In fact, as always, it was only necessary to devote a little time to the theory. Everything turned out to be simple and quite interesting. The result was the implementation of the curves in javascript using canvas.
Who cares how to build this winding beast welcome under the cut!
Some theory
Let's start with the principle of construction. The Bezier curve is constructed on several reference points. Figuratively speaking: the curve starts at the zero reference point, begins to move to the first, but suddenly notices the second - starts to touch it, smoothly changes its route in its direction, and then a third appears on the horizon, even more attractive ... And so passing by points, the curve stops its choice at the last reference point, where it comes. The path turns out like an alcoholic going home in the morning.

')
From the lyrics go to the harsh mathematics.
The theory is brazenly borrowed from Wikipedia :
The Bezier curve is a special case of Bernstein polynomials, is a parametric curve and is given by the expression:
 where
wheren is the number of reference points;
i is the number of the reference point;
t is the step at which we consider the position of the curve. For example, when building a curve using 100 points, the step will be 0.01 (not the reference, but points on the curve itself);
P - in our case, the coordinate of the reference point;
b (t) is the basic function of the Bezier curve. This coefficient determines the weight of the reference point. The Bernstein polynom itself is:

where
 Is the number of combinations of n through i , where n is the degree of the polynomial, i is the sequence number of the reference vertex.
Is the number of combinations of n through i , where n is the degree of the polynomial, i is the sequence number of the reference vertex.In the first and last steps, the value of the Bernstein polynomial is 1, the explanation is here . The midpoint of the curve is most influenced by the middle reference points, in the first third - the reference points of the first third, and so on. Bernstein polynom takes values from 0 to 1.
And so, to calculate the coordinate of the Bezier curve, we need:
- Calculate the weight of the reference point;
- Multiply the weight by the coordinate of this reference point;
- Repeat steps 1-2 for all anchor points;
- Add the resulting values - this will be the coordinate of the curve.
With the theory sort of figured out, go to the practice.
Hooray! Practice.
We consider the basic function:
// i - , n - , t - ( 0 1) function getBezierBasis(i, n, t) { // function f(n) { return (n <= 1) ? 1 : n * f(n - 1); }; // i- return (f(n)/(f(i)*f(n - i)))* Math.pow(t, i)*Math.pow(1 - t, n - i); } Next we get the coordinates of the curve.
You can build a Bezier curve in three-dimensional, four-dimensional space, and so on, but we will stop on a plane.
// arr - . - , (x = arr[0], y = arr[1]) // step - (0 < step < 1), 0.01 function getBezierCurve(arr, step) { if (step == undefined) { step = 0.01; } var res = new Array() for (var t = 0; t < 1 + step; t += step) { if (t > 1) { t = 1; } var ind = res.length; res[ind] = new Array(0, 0); for (var i = 0; i < arr.length; i++) { var b = getBezierBasis(i, arr.length - 1, t); res[ind][0] += arr[i][0] * b; res[ind][1] += arr[i][1] * b; } } return res; } Draw a curve:
// ctx - rendering context , arr - // delay - , pause - , function drawLines(ctx, arr, delay, pause) { if (delay == undefined) { delay = 10; } if (pause == undefined) { pause = delay; } var i = 0; function delayDraw() { if (i >= arr.length - 1) { return; } ctx.moveTo(arr[i][0],arr[i][1]); ctx.lineTo(arr[i+1][0],arr[i+1][1]); ctx.stroke(); ++i; setTimeout(delayDraw, delay); } setTimeout(delayDraw, pause); } It's time to try:
drawC = document.getElementById('bezier'); drawC.width = document.width - 30; drawC.height = document.height - 30; if (drawC && drawC.getContext) { ctx = drawC.getContext('2d'); ctx.fillStyle="#33CC99"; ctx.lineWidth=0.1; var flow; // var arr = new Array(); arr[0] = new Array(0, 100); arr[1] = new Array(100, 80); arr[2] = new Array(150, 150); arr[3] = new Array(200, 155); flow = getBezierCurve(new Array(arr[0], arr[1], arr[2], arr[3]), 0.01); drawLines(ctx, flow, 10); } Jsfiddle example
Related Links:
Article on javascript.ru
upd: The HTML5 standard supports quadraticCurveTo and bezierCurveTo methods for building Bezier curves by three and four points, respectively. Thank you lany .
Source: https://habr.com/ru/post/163073/
All Articles