Basics in SciLab. On the example of exam questions on CSVE
Tomorrow I will take an exam on a subject such as KSVE (Computer Service Computing Experiment). And the best way to prepare is to write an article. I will review some of the exam questions that are related to SciLab.
The article is more suitable for students using scilab to test a solution, for or for passing an exam on the discipline of the KSVE. For a more detailed study, you should read the literature listed at the end of the article.
Basic terms
Scilab (read by Saylab) is a package of applied mathematical programs that provides a powerful open environment for engineering (technical) and scientific calculations.
CeCILL (from “CEA CNRS INRIA Logiciel Libre”) is a free software license adapted to French and international law, similar to the GNU General Public License and still compatible with it.
A system of m linear algebraic equations with n unknowns (or, a linear system, also abbreviated as SLAU) in linear algebra is a system of equations of the form

Ordinary differential equations (ODE) is a differential equation of the form
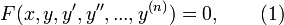
where is an unknown function (possibly a vector function, then, as a rule, also a vector function with values in space of the same dimension; in this case they speak of a system of differential equations) depending on the independent variable, the prime means differentiation with respect to. The number (the order of the highest derivative entering this equation) is called the order of the differential equation (1)
1. Computer math system SciLab: History of development. Features and key features. Advantages and disadvantages.
Story
Since 1994, distributed with source code via the Internet. In 2003, the Scilab Consortium was created to support Scilab. Now it includes 25 participants, including Mandriva, INRIA and ENPC (France).
')
Opportunities
Scilab contains hundreds of mathematical functions, and there is the possibility of adding new ones written in various languages (C, C ++, Fortran, etc.). There are also various data structures (lists, polynomials, rational functions, linear systems), an interpreter, and a high-level language.
Scilab was designed as an open system, and users can add their own data types and operations to it by overloading.
Many tools are available in the system:
2D and 3D graphics, animation
Linear algebra, sparse matrices (sparse matrices)
Polynomial and rational functions
Interpolation, approximation
Simulation: TAC and Remote Control Solution
Scicos: a hybrid system for modeling dynamic systems and simulation
Differential and non-differential optimizations
Signal processing
Parallel work
Statistics
Work with computer algebra
Interface to Fortran, Tcl / Tk, C, C ++, Java, LabVIEW
Scilab has a programming language similar to MATLAB. The package includes a utility that allows you to convert documents Matlab in Scilab.
Scilab allows you to work with elementary and a large number of special functions (Bessel, Neumann, integral functions), has powerful tools for working with matrices, polynomials (including symbolically), perform numerical calculations (for example, numerical integration) and solving problems of linear algebra, optimization and simulation, powerful statistical functions, as well as a tool for building and working with graphs.
For numerical calculations used libraries Lapack, LINPACK, ODEPACK, Atlas and others.
The package also includes Scicos - a tool for editing block diagrams and simulations (similar to simulink in the MATLAB package). Scilab can work with LabVIEW.
Key features
Differences from some commercial programs:
Free
Free (since version 5.0).
Small size - the distribution of version 4 took less than 20 MB against a more than two GB MATLAB package. The installer version 5 (5.4.0) increased in volume to 108 MB.
Ability to run in the console without using a graphical interface, including in the version for Windows (in UNIX and Windows versions of MatLab, this feature is also present). This allows automated calculations, there is a batch mode.
Advantages and disadvantages
The search for advantages and disadvantages on the Internet has not given anything. So talk about what I noticed myself.
If we talk about the merits, then the most basic for me is the free of charge of this package, compared to the same Mathematic, when to perform laboratory work I had to look for a serial or crack. Next is cross-platform, because I prefer to use Gentoo than Windows. In principle, most of the advantages are described in Key Features.
Of the shortcomings, I see only 2: This is not such a visualization of programming as in Mathematic, and the system also uses primarily numerical approaches to calculate, which can affect accuracy.
2. Basics of working in SciLab. User and system variables. Mathematical expressions. Comments
When writing this article I use the version of scilab-5.3.3 under windows.
SciLab 5.3.3
Operating systems: Windows, Linux, MacOS
User and system variables
Year / Release Date: 2011
Version: 5.3.3
Developer: Free Open Source Software for Numerical Computation
Developer website: www.scilab.org
Digit capacity: 32bit + 64bit
License: CeCILL
According to the characteristics of the data is not found, but I can say that this package is loaded without glitches on my laptop
Processor: Intel Celeron Dual-Core T3300 2.0 GHz
2GB DDR3 RAM
Intel GMA4500M Video Adapter
Before proceeding further, consider the interface itself. At startup, a command window opens.

There are 2 ways to work: 1 - this is work in the same command window, 2 - open SciNotes (something like a backlit notebook) where you can write code that you can run later, the result will appear in the command window.
For example, I will review the output of Hellow world.
Command line. We use the display function disp ()

When working in SciNotes, you get something similar

to execute the code, it is necessary or click on the arrow in the right :) (as in many development environments)
or Execute-> ... without displaying commands
in principle, you can use other methods of execution, and not use the output on the screen
The result of the execution will be:

because we can say that the interface has been studied, then I will give just the code and the result of the execution
SciLab is registry sensitive, i.e. A and a are different variables.
Basic operations:
+ addition
- subtraction
* multiplication
/ division on the right, i.e. x / y = xy ^ (- 1)
\ division on the left, i.e. x \ y = x ^ (- 1) y
^ exponentiation, i.e. x ^ y
** exponentiation (equivalent to ^)
'Hermitian conjugation (complex conjugation and transposition)
3. Basics of working in SciLab. Functions and their types. Ways of declaring custom functions. Using functions. Script files and their use for storing functions.
Elementary math functions.
types in SciLab
iconvert convert to integer representation
inttype integer type definition
The easiest way to call a custom function is:
example of custom function:
Save it. The following is an example of calling this function.
4. Definition of one-dimensional and multidimensional arrays. Basic operations on arrays.
An example of how to define a one-dimensional array:
Specifying a two-dimensional array:
square brackets ”[” and ”]” indicate the beginning and end of the enumeration
matrix elements
the comma ”,” separates the matrix elements that are in one line,
semicolon ";" separates the rows of the matrix.
size determine the size of the matrix
matrix change matrix size
resize_matrix create a new matrix of a given size and copy
into it elements from the original matrix
Matrix operations:
Appeal to the elements of the matrix
i = 1; 2, a j = 3; four
for this, we take a ready-made matrix
A whole matrix
A (:, :) whole matrix
A (i: j, k) elements of the matrix in the k-th column from the i-th to j-th row
A (i, j: k) elements of the matrix in the i-th row from j-th to k-th column
A (i, :) i-th row of the matrix
A (:, j) jth column of the matrix
Generate the identity matrix
Matrix Operations
+ addition. + elementwise addition
- subtraction. - elementwise subtraction
* multiplication. * elementwise multiplication
/ division on the right ./ elementwise division on the right
\ division on the left. \ elementwise division on the left
^ or * exponentiation: ^ elementwise exponentiation
'Hermitian conjugation (complex conjugation and transposition)
. ' transpose without pairing
an example of multiplying a number by a 2 by 2 matrix
5. Definition of one-dimensional and multidimensional arrays. Special matrix functions
matrix functions
chol decomposition of cholester
companion accompanying matrix
cond condition number
det matrix determinant
inv inverse matrix
linsolve solving linear equation systems
lsq least squares method
lu LU decomposition with a choice of support element
qr QR decomposition
rcond inverse condition number
spec eigenvalues and vectors
svd matrix singular number decomposition
testmatrix generation of special matrices (Hilbert, Frank, etc.)
trace trace matrix
6. Definition of one-dimensional and multi-dimensional arrays. Decision SLAU. Character arrays and operations on them
The text of the script file with the solution of the Kramer formula
Gauss system solution
7. Numerical integration. Approaches to integration. Integration of user-defined functions
Numerical integration (historical name: (numerical) quadrature) - calculation of the value of a definite integral (as a rule, approximate). By numerical integration is understood a set of numerical methods for finding the value of a definite integral.
Trapezoid Integration
let's integrate the function, the root of 2 * x-1 on the interval from 1 to 10 with a partition in 1 step
The quadrature formulas of Newton Cotes
8. Numerous differentiation. Approaches to differentiation.
Numerical differentiation is a set of methods for calculating the value of the derivative of a discretely given function.
The basis of numerical differentiation is the approximation of the function, from which the derivative is taken, by an interpolation polynomial. All the basic formulas of numerical differentiation can be obtained using the first Newton interpolation polynomial (Newton's formula for the beginning of the table).
at the point
on the segment
and check
9. Solution of ODE using SciLab. Functions used to solve ODE. The decision of boundary problems.
There are 4 ways to solve an ODE:
1. With the help of the ode command, which is a solver for solving ordinary
differential equation.
2. Using the odedc command, which calculates the solution of mixed discrete
continuous system.
3. The dassl command, which gives a solution to an implicitly expressed differential equation.
4. Using the impl command, which gives a solution to an implicitly expressed linear
differential equation.
Example:
the result is such a schedule

for one you can see the graphic window. Plotting will be discussed in detail below.
10. Construction of two-dimensional graphs in the SciLab system. The main features and types of graphs.
Plot function
Consider an example:
as you can see, the first parameter of the function is a segment, and the second function
it is also possible to draw several functions at once if you list them:

Plot2d function
Consider the function again with an example:

as we can see, this function has much more functionality.
Functions are transmitted immediately by an array, you can also specify the color of the lines and the segment.
Polarplot function
It is used to build a graph in polar coordinates.
chamomile turns out

parameters are similar as in the case of plot2d
11. Construction of three-dimensional graphs in the SciLab system. The main features and types of graphs.
There are 4 ways to build a graph:
Method 1.
Using the command plot3d. The team creates a 3D graph based on the points specified by the matrix
x, y and z.
Method 2
Using the plot3d1 command. The team creates a 3D graph at the points specified
x, y and z matrices using color levels. The thing is generally redundant: magnitude
The z coordinates are also colored, depending on the received value.
z.
Method 3.
Using the fplot3d command. This is an analogue of the fplot3d command, but the imaged surface
set by external function.
Method 4.
Using the fplot3d1 command. This is an analogue of the command plot3d1, but the imaged surface
set by external function.
See the help syntax for these commands.
Example 1

I forgot to specify that in the graphics window there is the ability to export data, i.e. save picture
Example2.

Example 3
The result is the same as in example 1.
Example 4
the result is the same as in example 2
12. The problem of polynomials in SciLab. Character operations with polynomials. Solving algebraic equations. Comparison of fsolve and roots functions.
Consider the example of solving the equation 2x ^ 4-8x ^ 3 + 8x ^ 2-1 = 0

The array indicates the coefficients for x
After constructing the polynomial, try to get the solution:
To solve the transcendental equations, use the function Scilab fsolve (x0, f)
task
I hope this article will serve as an impetus for further study of SciLab or solving your tasks / laboratories
List of sources used:
1. http://en.wikipedia.org/wiki/Scilab
2. http://vse-o-scilab.narod.ru/osnovi_raboti_v_scilab/konsol_scilab/
3. Introduction to Scilab Micha¨el Baudin Translation Artem Glebov November 2010
4. Alekseev E.R., Chesnokova O.V. Arrays and matrices in Scilab. Solving linear algebra problems.
The article is more suitable for students using scilab to test a solution, for or for passing an exam on the discipline of the KSVE. For a more detailed study, you should read the literature listed at the end of the article.
Basic terms
Scilab (read by Saylab) is a package of applied mathematical programs that provides a powerful open environment for engineering (technical) and scientific calculations.
CeCILL (from “CEA CNRS INRIA Logiciel Libre”) is a free software license adapted to French and international law, similar to the GNU General Public License and still compatible with it.
A system of m linear algebraic equations with n unknowns (or, a linear system, also abbreviated as SLAU) in linear algebra is a system of equations of the form

Ordinary differential equations (ODE) is a differential equation of the form
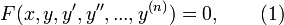
where is an unknown function (possibly a vector function, then, as a rule, also a vector function with values in space of the same dimension; in this case they speak of a system of differential equations) depending on the independent variable, the prime means differentiation with respect to. The number (the order of the highest derivative entering this equation) is called the order of the differential equation (1)
1. Computer math system SciLab: History of development. Features and key features. Advantages and disadvantages.
Story
Since 1994, distributed with source code via the Internet. In 2003, the Scilab Consortium was created to support Scilab. Now it includes 25 participants, including Mandriva, INRIA and ENPC (France).
')
Opportunities
Scilab contains hundreds of mathematical functions, and there is the possibility of adding new ones written in various languages (C, C ++, Fortran, etc.). There are also various data structures (lists, polynomials, rational functions, linear systems), an interpreter, and a high-level language.
Scilab was designed as an open system, and users can add their own data types and operations to it by overloading.
Many tools are available in the system:
2D and 3D graphics, animation
Linear algebra, sparse matrices (sparse matrices)
Polynomial and rational functions
Interpolation, approximation
Simulation: TAC and Remote Control Solution
Scicos: a hybrid system for modeling dynamic systems and simulation
Differential and non-differential optimizations
Signal processing
Parallel work
Statistics
Work with computer algebra
Interface to Fortran, Tcl / Tk, C, C ++, Java, LabVIEW
Scilab has a programming language similar to MATLAB. The package includes a utility that allows you to convert documents Matlab in Scilab.
Scilab allows you to work with elementary and a large number of special functions (Bessel, Neumann, integral functions), has powerful tools for working with matrices, polynomials (including symbolically), perform numerical calculations (for example, numerical integration) and solving problems of linear algebra, optimization and simulation, powerful statistical functions, as well as a tool for building and working with graphs.
For numerical calculations used libraries Lapack, LINPACK, ODEPACK, Atlas and others.
The package also includes Scicos - a tool for editing block diagrams and simulations (similar to simulink in the MATLAB package). Scilab can work with LabVIEW.
Key features
Differences from some commercial programs:
Free
Free (since version 5.0).
Small size - the distribution of version 4 took less than 20 MB against a more than two GB MATLAB package. The installer version 5 (5.4.0) increased in volume to 108 MB.
Ability to run in the console without using a graphical interface, including in the version for Windows (in UNIX and Windows versions of MatLab, this feature is also present). This allows automated calculations, there is a batch mode.
Advantages and disadvantages
The search for advantages and disadvantages on the Internet has not given anything. So talk about what I noticed myself.
If we talk about the merits, then the most basic for me is the free of charge of this package, compared to the same Mathematic, when to perform laboratory work I had to look for a serial or crack. Next is cross-platform, because I prefer to use Gentoo than Windows. In principle, most of the advantages are described in Key Features.
Of the shortcomings, I see only 2: This is not such a visualization of programming as in Mathematic, and the system also uses primarily numerical approaches to calculate, which can affect accuracy.
2. Basics of working in SciLab. User and system variables. Mathematical expressions. Comments
When writing this article I use the version of scilab-5.3.3 under windows.
SciLab 5.3.3
Operating systems: Windows, Linux, MacOS
User and system variables
Year / Release Date: 2011
Version: 5.3.3
Developer: Free Open Source Software for Numerical Computation
Developer website: www.scilab.org
Digit capacity: 32bit + 64bit
License: CeCILL
According to the characteristics of the data is not found, but I can say that this package is loaded without glitches on my laptop
Processor: Intel Celeron Dual-Core T3300 2.0 GHz
2GB DDR3 RAM
Intel GMA4500M Video Adapter
Before proceeding further, consider the interface itself. At startup, a command window opens.

There are 2 ways to work: 1 - this is work in the same command window, 2 - open SciNotes (something like a backlit notebook) where you can write code that you can run later, the result will appear in the command window.
For example, I will review the output of Hellow world.
Command line. We use the display function disp ()

When working in SciNotes, you get something similar

to execute the code, it is necessary or click on the arrow in the right :) (as in many development environments)
or Execute-> ... without displaying commands
in principle, you can use other methods of execution, and not use the output on the screen
The result of the execution will be:

because we can say that the interface has been studied, then I will give just the code and the result of the execution
SciLab is registry sensitive, i.e. A and a are different variables.
a = 1, A = 3
// Each operation starts on a new line or separated by commas.
// comments can be left after two symbolic slash
b = 3
c = a + b
disp ©
Basic operations:
+ addition
- subtraction
* multiplication
/ division on the right, i.e. x / y = xy ^ (- 1)
\ division on the left, i.e. x \ y = x ^ (- 1) y
^ exponentiation, i.e. x ^ y
** exponentiation (equivalent to ^)
'Hermitian conjugation (complex conjugation and transposition)
3. Basics of working in SciLab. Functions and their types. Ways of declaring custom functions. Using functions. Script files and their use for storing functions.
Elementary math functions.
acos acosd acosh acoshm acosm acot acotd acoth
acsc acscd acsch asec asecd asech asin asind
asinh asinhm asinm atan atand atanh atanhm atanm
cos cosd cosh coshm cosm cotd cotg coth
cothm csc cscd csch sec secd sech sin
sinc sind sinh sinhm sinm tan tand tanh
tanhm tanm
exp expm log log10 log1p log2 logm max
maxi min mini modulo pmodulo sign signm sqrt
sqrtm
types in SciLab
y = int8 (x) 8-bit number with the sign [-2 ^ 7; (2 ^ 7) -1] = [-128; 127]
y = uint8 (x) is an 8-bit unsigned [0; (2 ^ 8) -1] = [0; 255]
y = int16 (x) 16-bit number with the sign [-2 ^ 15; (2 ^ 15) -1] = [-32768; 32767]
y = uint16 (x) 16-bit unsigned [0; (2 ^ 16) -1] = [0; 65535]
y = int32 (x) 32-bit number with the sign [-2 ^ 31; (2 ^ 31) -1] = [-2147483648; 2147483647]
y = uint32 (x) 32-bit unsigned [0; (2 ^ 32) -1] = [0; 4294967295]
iconvert convert to integer representation
inttype integer type definition
The easiest way to call a custom function is:
outvar = myfunction (invar)
example of custom function:
function y = myfunction (x)
y = 2 * x
endfunction
Save it. The following is an example of calling this function.
-> exec ('D: \ PRIVATE \ Learning \ KSVE \ myfunction.sci', -1)
-> y = myfunction (3)
y =
6
4. Definition of one-dimensional and multidimensional arrays. Basic operations on arrays.
An example of how to define a one-dimensional array:
-> A = [1, 2, 3, 4, 5, 6]
A =
1. 2. 3. 4. 5. 6.
Specifying a two-dimensional array:
-> A = [1, 2, 3; 4, 5, 6]
A =
1. 2. 3.
4. 5. 6.
square brackets ”[” and ”]” indicate the beginning and end of the enumeration
matrix elements
the comma ”,” separates the matrix elements that are in one line,
semicolon ";" separates the rows of the matrix.
size determine the size of the matrix
matrix change matrix size
resize_matrix create a new matrix of a given size and copy
into it elements from the original matrix
Matrix operations:
Appeal to the elements of the matrix
i = 1; 2, a j = 3; four
for this, we take a ready-made matrix
-> A = testmatrix ("hilb", 5)
A =
25. - 300. 1050. - 1400. 630.
- 300. 4800. - 18900. 26880. - 12600.
1050. - 18900. 79380. - 117600. 56700.
- 1400. 26880. - 117600. 179200. - 88200.
630. - 12600. 56700. - 88200. 44100.
-> A (1: 2, 3: 4)
ans =
1050. - 1400.
- 18900. 26880
A whole matrix
A (:, :) whole matrix
A (i: j, k) elements of the matrix in the k-th column from the i-th to j-th row
A (i, j: k) elements of the matrix in the i-th row from j-th to k-th column
A (i, :) i-th row of the matrix
A (:, j) jth column of the matrix
Generate the identity matrix
-> A = ones (3, 3)
A =
1. 1. 1.
1. 1. 1.
1. 1. 1.
Matrix Operations
+ addition. + elementwise addition
- subtraction. - elementwise subtraction
* multiplication. * elementwise multiplication
/ division on the right ./ elementwise division on the right
\ division on the left. \ elementwise division on the left
^ or * exponentiation: ^ elementwise exponentiation
'Hermitian conjugation (complex conjugation and transposition)
. ' transpose without pairing
an example of multiplying a number by a 2 by 2 matrix
-> B = 2 * ones (2, 2)
B =
2. 2.
2. 2.
5. Definition of one-dimensional and multidimensional arrays. Special matrix functions
matrix functions
chol decomposition of cholester
companion accompanying matrix
cond condition number
det matrix determinant
inv inverse matrix
linsolve solving linear equation systems
lsq least squares method
lu LU decomposition with a choice of support element
qr QR decomposition
rcond inverse condition number
spec eigenvalues and vectors
svd matrix singular number decomposition
testmatrix generation of special matrices (Hilbert, Frank, etc.)
trace trace matrix
6. Definition of one-dimensional and multi-dimensional arrays. Decision SLAU. Character arrays and operations on them
The text of the script file with the solution of the Kramer formula
-> A = [2 1 -5 1; 1 -3 0 -6; 0 2 -1 2; 1 4 -7 6]; // Matrix of coefficients
-> b = [8; 9; -5; 0]; // Vector of free coefficients
-> // First auxiliary matrix
-> A1 = A; A1 (:, 1) = b;
-> // The second auxiliary matrix
-> A2 = A; A2 (:, 2) = b;
-> // Third Auxiliary Matrix
-> A3 = A; A3 (:, 3) = b;
-> // Fourth auxiliary matrix
-> A4 = A; A4 (:, 4) = b;
-> // The main determinant is non-zero
-> D = det (A);
-> // Auxiliary matrix determinants
-> d (1) = det (A1);
-> d (2) = det (A2);
-> d (3) = det (A3);
-> d (4) = det (A4);
-> // Vector of unknowns
-> x = d / D
x =
3
- four.
- one.
one.
-> // Check
-> P = A * xb
P =
0
0
- 8.882D-16
2.665D-15
Gauss system solution
-> A = [2 -1 1; 3 2 -5; 1 3 -2];
-> b = [0; 1; 4];
-> // Reduction of the expanded matrix to a triangular view
-> C = rref ([ab]);
-> // Select the last column from the matrix,
-> // x - system solution
-> x = C (1: 3,4: 4)
x =
0.4642857
1.6785714
0.75
-> A * x // Check
ans =
- 5.551D-16
one.
four.
7. Numerical integration. Approaches to integration. Integration of user-defined functions
Numerical integration (historical name: (numerical) quadrature) - calculation of the value of a definite integral (as a rule, approximate). By numerical integration is understood a set of numerical methods for finding the value of a definite integral.
Trapezoid Integration
let's integrate the function, the root of 2 * x-1 on the interval from 1 to 10 with a partition in 1 step
-> x = 1: 10
x =
1. 2. 3. 4. 5. 6. 7. 8. 9. 10.
-> y = sqrt (2 * x-1)
y =
column 1 to 6
1. 1.7320508 2.236068 2.6457513 3. 3.3166248
column 7 to 10
3.6055513 3.8729833 4.1231056 4.3588989
-> inttrap (x, y)
ans =
27.211585
The quadrature formulas of Newton Cotes
-> integrate ('(2 * x-1) ^ 0.5', 'x', 5.13)
ans =
32.666667
8. Numerous differentiation. Approaches to differentiation.
Numerical differentiation is a set of methods for calculating the value of the derivative of a discretely given function.
The basis of numerical differentiation is the approximation of the function, from which the derivative is taken, by an interpolation polynomial. All the basic formulas of numerical differentiation can be obtained using the first Newton interpolation polynomial (Newton's formula for the beginning of the table).
at the point
-> function f = myf (x), f = (x + 2) ^ 3 + 5 * x, endfunction;
-> numdiff (myf, 1)
ans =
32.
-> x = 1; 3 * (x + 2) ^ 2 + 5
ans =
32.
on the segment
v = 0: 3;
-> numdiff (my, v)
ans =
17. 0. 0. 0.
0. 32. 0. 0.
0. 0. 52.999999 0.
0. 0. 0. 80.000002
and check
-> function f1 = my1 (x), f1 = 3 * (x + 2) ^ 2 + 5, endfunction;
-> my1 (v)
ans =
17. 32. 53. 80.
9. Solution of ODE using SciLab. Functions used to solve ODE. The decision of boundary problems.
There are 4 ways to solve an ODE:
1. With the help of the ode command, which is a solver for solving ordinary
differential equation.
2. Using the odedc command, which calculates the solution of mixed discrete
continuous system.
3. The dassl command, which gives a solution to an implicitly expressed differential equation.
4. Using the impl command, which gives a solution to an implicitly expressed linear
differential equation.
Example:
-> y0 = 1;
-> t0 = 1;
-> t = 1: 0.01: 1.5;
-> deff ("[ydot] = f (t, y)", "ydot = y ^ (1/3) * t")
-> y = ode (y0, t0, t, f);
-> y_exact = ((t ^ 2 + 2) / 3) ^ (1.5); // this is the function of the exact solution for comparison
-> my_er = y-y_exact;
-> plot (t, y-y_exact) // is a graph of the computation error from the argument t
the result is such a schedule

for one you can see the graphic window. Plotting will be discussed in detail below.
10. Construction of two-dimensional graphs in the SciLab system. The main features and types of graphs.
Plot function
Consider an example:
x = -2 *% pi: 0.1: 2 *% pi;
y = sin (cos (x));
plot (x, y);
as you can see, the first parameter of the function is a segment, and the second function
it is also possible to draw several functions at once if you list them:
x = -6.28: 0.02: 6.28;
y = sin (x / 2);
z = cos (x);
v = exp (cos (x));
plot (x, y, x, z, x, v);

Plot2d function
Consider the function again with an example:
x = [- 2 *% pi: 0.1: 2 *% pi];
y = [sin (x); cos (x)];
plot2d (x, y ', style = [color ("red"), color ("blue")], rect = [- 8, -2,8,2])

as we can see, this function has much more functionality.
Functions are transmitted immediately by an array, you can also specify the color of the lines and the segment.
Polarplot function
It is used to build a graph in polar coordinates.
fi = 0: 0.01: 2 *% pi;
ro = 3 * cos (5 * fi);
ro1 = 3 * cos (3 * fi);
polarplot (fi, ro, style = color ("red"));
chamomile turns out

parameters are similar as in the case of plot2d
11. Construction of three-dimensional graphs in the SciLab system. The main features and types of graphs.
There are 4 ways to build a graph:
Method 1.
Using the command plot3d. The team creates a 3D graph based on the points specified by the matrix
x, y and z.
Method 2
Using the plot3d1 command. The team creates a 3D graph at the points specified
x, y and z matrices using color levels. The thing is generally redundant: magnitude
The z coordinates are also colored, depending on the received value.
z.
Method 3.
Using the fplot3d command. This is an analogue of the fplot3d command, but the imaged surface
set by external function.
Method 4.
Using the fplot3d1 command. This is an analogue of the command plot3d1, but the imaged surface
set by external function.
See the help syntax for these commands.
Example 1
t = -% pi: 0.3:% pi;
plot3d (t, t, sin (t) '* cos (t), 35.45,' X @ Y @ Z ', [2,2,4]);

I forgot to specify that in the graphics window there is the ability to export data, i.e. save picture
Example2.
t = -% pi: 0.3:% pi;
plot3d1 (t, t, sin (t) '* cos (t), 35.45,' X @ Y @ Z ', [2,2,4]);

Example 3
deff ('[z] = surf (x, y)', 'z = sin (x) * cos (y)');
t = -% pi: 0.3:% pi;
fplot3d (t, t, surf, 35.45, "X @ Y @ Z");
The result is the same as in example 1.
Example 4
deff ('[z] = surf (x, y)', 'z = sin (x) * cos (y)');
t = -% pi: 0.3:% pi;
fplot3d1 (t, t, surf, 35.45, “X @ Y @ Z”);
the result is the same as in example 2
12. The problem of polynomials in SciLab. Character operations with polynomials. Solving algebraic equations. Comparison of fsolve and roots functions.
Consider the example of solving the equation 2x ^ 4-8x ^ 3 + 8x ^ 2-1 = 0
V = [- 1 0 8 -8 2];
p = poly (V, 'x', 'c')

The array indicates the coefficients for x
After constructing the polynomial, try to get the solution:
X = Rooses (p)
X =
2.306563
1.5411961
- 0.3065630
0.4588039
To solve the transcendental equations, use the function Scilab fsolve (x0, f)
task

-> deff ('[y] = f1 (x)', 'y1 = ((x-1) ^ 2) ^ (1/3), y2 = (x ^ 2) ^ (1/3), y = y1-y2 ')
-> fsolve (0, f1)
ans =
0.5
I hope this article will serve as an impetus for further study of SciLab or solving your tasks / laboratories
List of sources used:
1. http://en.wikipedia.org/wiki/Scilab
2. http://vse-o-scilab.narod.ru/osnovi_raboti_v_scilab/konsol_scilab/
3. Introduction to Scilab Micha¨el Baudin Translation Artem Glebov November 2010
4. Alekseev E.R., Chesnokova O.V. Arrays and matrices in Scilab. Solving linear algebra problems.
Source: https://habr.com/ru/post/162889/
All Articles