The dependence of transparency on the orientation of the surface

The other day, twirling a plastic cup in my hands, I noticed that the apparent transparency of plastic depends on the angle at which you look at the surface - if you look perpendicular to the surface, the background is clearly visible, and if you look along the surface, the material becomes almost opaque. I was interested in this phenomenon, and I decided to build a mathematical model.

No sooner said than done. Under the cut, the output of the formula, the fragment shader code and a small demo.

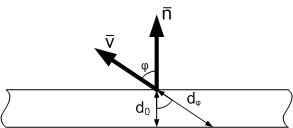
We assume that the material is homogeneous optical - its optical properties do not depend on direction. Then the change in transparency is caused by different lengths of the path of the light beam in the thickness of the material.


')
where - unit surface normal vector, - single direction vector to the observer.

Let the apparent transparency of the material is determined by the opacity coefficient, which determines the mixing of the material color with the background color as follows:

Let's see how the value depends on the thickness of the material. To do this, we divide the layer of material with thickness and opacity coefficient on layers of equal thickness each with opacity coefficient . Let be - background color, - the color of the material, and - the color of the output of each layer.



But also , and consequently:


Those. with increasing thickness, the apparent transparency of the material decreases exponentially.

Let the thickness , then:


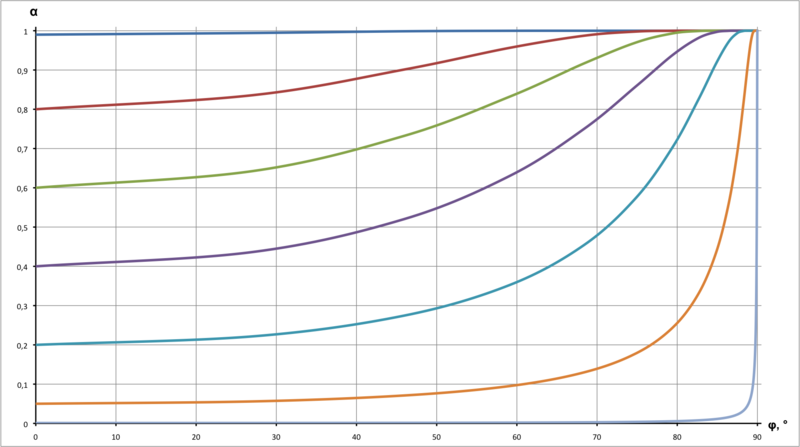
So, the required formula:



Below is the fragment shader code that implements this formula:

varying vec4 v_color; varying vec3 v_normal; varying vec3 v_eye; void main(void) { //         float cosPhi = dot(v_normal, v_eye) / sqrt( dot(v_normal, v_normal) * dot(v_eye, v_eye) ); //    ,        //     ,      // 0.999 ^ 10000 = 4.5173346E-5 float alpha = 1.0 - pow(1.0 - v_color.a, 1.0 / max(abs(cosPhi), 0.00001)); gl_FragColor = vec4(vec3(v_color), alpha); }; 

The result is this:


The source code of the demo application is available on bitbucket.org