I planned to write about some kind of mega-mind, if not about an even-odd sort of Butcher merge, then, at worst, about sorting with a Cartesian tree. But then I remembered that a series of celebrations is coming, which means that it’s worth offering something festive, I would even say frivolous.


')

David Morgan-Mar

Australian fun geek, astrophysicist, mathematician, programmer and inventor. I managed to work at IBM, now an employee of Canon. A lover of comics, "Star Wars", travel, abnormal coding, worlds GURPS. Author of several esoteric programming languages ​​( Chef , ZOMBIE, Piet , etc.).

On the personal site of David Morgan-Mara there is a small selection of “esoteric sorts”, which is a sin not to tell.

Abacus sorting
(Abacus sort)

Suppose you need to sort a set of natural numbers. We will lay them out under each other in the form of horizontal rows of pebbles in an appropriate amount. Shift vertically until it stops.

Actually that's all.

If we count the pebbles in each horizontal row, we get the initial set of numbers in an ordered state.

I have already written in detail about this sorting, so we immediately move on to the next one.

Bog sorting (Bogobogosort)

Traditionally, the slowest sorting is the so-called bog sorting (Bogosort).



Mix the array until its elements are ordered. The time complexity is O (nxn!).

Of course, any exceptionally slow algorithm can be made even less productive. If tail recursion is added to Bogosort when testing subarrays for orderliness, then even the most dying swamp can be drowned in an even bigger quagmire. Well, if you still recursively clone the checked subarrays and sort them until they match the original, then much can be achieved in memory complexity.

The basic procedure is the same as with Bogosort:

1. Check if the array is sorted.
2. If not, then mix it up and return to paragraph 1.

But checking the array for ordering is as follows:

1. A copy of the array is created.
2. The first n-1 elements of the copy are sorted using Bogobogosort.
3. It is checked whether the nth element in the copy is greater than the first n-1 elements.
4. If not, shuffle the copy of the array and return to step 2.
5. If yes, then you need to check whether the copy is the same as the original. If it is the same, then the array is sorted in any way, if not, then we mix up the copy of the array and go to step 2.

Such a sophisticated mockery of the data practically guarantees that the process will continue for a very long time.



As for the complexity of the time, David believes that somewhere of order O (n! ^N! ). When testing on an array of 7 elements of the final result, he did not wait.

Maxwell's Demon Sort

The sorting method is based on the famous thought experiment of the great English physicist of the XIX century, James Clerk Maxwell. This method of hardware implementation, based on the current achievements of science and technology, is quite problematic.

The gas tank is divided into two halves by an impenetrable wall. In the wall there is a hole, which is equipped with a special device, which we call Maxwell's demon. The demon is arranged in such a way that through the hole it only passes fast (hot) gas molecules from the left to the right, and slow (cold) molecules from the right to the left.

As a result of the functioning of this system, a paradox allegedly arises that violates the second law of thermodynamics: in the vessel solely due to the internal energy, without attracting additional, the left part cools and the right part heats up.



Take a vessel with a gas and consider all molecules as an unsorted set of numbers (each of which is a kind of energy map of the molecule). We will partition the vessel with the wall with Maxwell's demon embedded in it. After some time, molecules will be collected in the right part of the vessel, whose energy exceeds a certain specified value (or is equal to it), and in the left part — molecules whose energy is less than this value.

We divide each half of the vessel into its halves using the walls with built-in Maxwell demons (for which other throughput values ​​are given). Thus, we additionally distribute molecules to even more “hot” and “cold” ones. And so we will divide the space inside the vessel with additional walls with built-in Maxwell demons until there are molecules with the same energy in each of its limited parts. At this point, all particles will be "sorted."

Jared Diamond's sort

Algorithm, based on Jared Diamond's Guns, Microbes, and Steel: The Fates of Human Civilizations (Guns, Germs, and Steel: The Fates of Human Societies).

This work, awarded the Pulitzer Prize, is the most significant work on geographical anthropology over the past decade and a half. The book was highly appreciated by sociologists, historians and demographers. Bill Gates, not the last person understanding global global processes, was also impressed: “Impressive ... This book lays the foundation for understanding the history of mankind”.

Due to the extensiveness of the aspects involved, even a brief retelling of the ideas presented in the book is not possible in the narrow framework of this short article. Those interested can easily find the book itself, as well as a 3-part documentary filmed in 2005 by National Geographic Channel, on the Internet.

Now the algorithm.

For each number from the sorted list, we define a primitive civilization of hunter-gatherers, the region of their deployment will be inhabited by wild animals (for subsequent domestication) and plants (for the development of agriculture). The size of each local human population, the species diversity of flora and fauna should be chosen in direct proportion to the corresponding number.

Let me develop agriculture, industry, science and culture. The society that invents and first begins to massively use firearms will correspond in the list to the largest element, with respect to which all others will eventually be ordered.

The execution time depends only on the value of the largest number, which allows one to formally assert about the time complexity O (1). At the moment, only one reliable case of using this sorting is known, the elapsed time was approximately 13000 years. This value would be smaller if the largest element in the array would be larger.

Sort Drops (Dropsort)

Cheap and angry: we pass through the array and along the way we delete (discard) unsorted items from it.



A very useful, by the way, hack with O (n) time complexity. You can not thank.

Sort "Tower of Hanoi" (Tower of Hanoi sort)

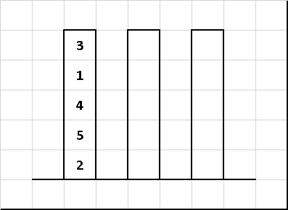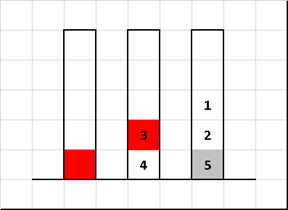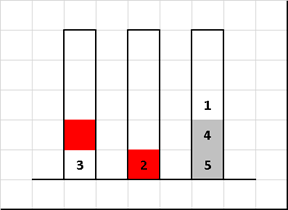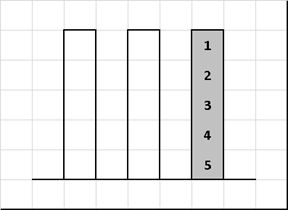
A sorting algorithm based on the famous puzzle of the French mathematician Edward Luc A.

We only change the input value - the disks on the first rod do not have to be in the order “smaller over large”. We will leave the rest of the rules as in the classics - we transfer only one disk at a time, and you should not put “pancakes” of a larger diameter on those that are smaller in size. It is required by transferring the disks from one rod to another as a result of collecting them in a sequence ordered by size.

This sorting is interesting because the degenerate case for it is ... a completely ordered array. Then we are dealing with a reference "hanoi" for which you need to perform 2 ⁿ -1 movements. The best case in time is reverse, in this case, the elements one by one immediately jump into place. And in general, the closer the array is to the sorted state, the worse - and vice versa!

Sorting Intelligent Design Sort

Since an array of size n is possible n! permutations of elements, the probability that the elements in it will follow exactly in the order in which they follow is equal to 1 / n! which is vanishingly small. It is absurd to argue that such a state of the array arose by chance.

It is much more logical to assume that there is some higher rational force that created the array and arranged the elements in it in a certain order. There is no reason to say that this order is not optimal. Most likely, the elements in the structure are already built precisely in the sequence in which it is necessary, even if this contradicts our mundane and imperfect notions of Order.

Moreover, any attempts to “sort” an array will most likely lead to a violation of the perfection originally embedded in it.