Estimates of software projects or is the whole the sum of the components?
The following cross-post (oh, I, beech!) From my main blog.
In this article, I'm going to talk about things that you all have known for a long time. Now I suggest to think about them. <? Xml: namespace prefix = o ns = "urn: schemas-microsoft-com: office: office" /> <o: p> </ o: p>
If you are not new to the software industry, then you are aware that from time to time, any manager finds himself in a phase when he becomes sharply interested in estimating time, work ... And usually, not by any means, but by some fashionable technique. You are asked to report in a week how long the bugs and the feature, which design has not yet managed to do, will take, not to mention the fact that the planned work certainly should be broken into pieces up to an hour, if you can’t be done every minute. .. <o: p> </ o: p>
How is time usually estimated for projects? Everyone knows that it’s impossible to estimate a large piece correctly, so it is broken up into smaller pieces, and then these smaller pieces are put together, for example, in some Gantt diagram or just on a calendar or Excel. <O: p> < / o: p>
')
Today I would like to talk about two completely wrong assumptions that underlie this technique. <O: p> </ o: p>
To begin with, what is the estimated time of the project or is there a project step? <O: p> </ o: p>
No, no, I understand that in the expectations of management, you, like Cassandra, must absolutely predict the future, and unlike Cassandra, this is not an example more optimistic, as business tenets demand (I don’t know how this thing translates, something like a moral code of a young builder of communism - we have to have training for it every year). In general, everyone understands that it is difficult, but your prophecies should be “good enough!” From all points of view. <O: p> </ o: p>
Well, when managers say so - this is understandable. But we are not managers, we are engineers, techies. We know that “good enough” is something very vague. And to be part of an engineering discipline, a concept must be measurable in numbers. That is, I want to somehow measure this matter in order to say distinctly “good enough” or still not “good enough”. And when an engineer wants to measure something, he applies such harmful science - mathematics. It’s harmful because it constantly talks about managers about what it thinks of them, and it’s also right ... <o: p> </ o: p>
So, what is the evaluation in mathematics, more precisely in the statistics and probability theory. And this is the interval in which the expected random variable with a given probability falls. A random variable is how long a project will take or there will be a separate project step. It seems that what is necessary, what the doctor prescribed, that's just what to do with a given probability? <O: p> </ o: p>
Try to approach the manager and say, “With a probability of 80 percent, this project will meet a month.” What will he tell you?
Yeah, have you already felt a slight indisposition? Further better. He wants “for sure”, but what does the mathematics say to this? Imagine a picture of some familiar distribution, say, a Poisson or normal Gaussian. What is the interval, the probability of falling into which is 100 percent? That's right, alas, if the manager wants a guaranteed estimate, then mathematically it is always infinity. Well, or practically, the period for which the project is simply beaten. Any project has a chance of failure. Good engineers, who were allowed to make good grades, have less chance of failure, and bad ones have much more, but still, under no circumstances, it is not zero. <O: p> </ o: p>
That is, volens-nolens will take off your estimates, which will be considered as your promise, although in reality they will be estimates for a probability of eighty, ninety, ninety-five percent ... <o: p> </ o: p>
So, the evaluation of a project or a project step is the time interval in which it will be packed with a probability that is comfortable for you. Or you can say with a comfortable risk for you not to meet. <O: p> </ o: p>
Suppose you choose 80 percent as such (respectively, the risk does not meet the 20 percent). Yes, I know, it sounds very risky, but watching programmers on natural conditions I had the feeling that even 80 percent for the majority are excessively high. Normally, smart managers multiply developer ratings at least one and a half to two times. <O: p> </ o: p>
So, you have a project, it has two steps. You estimate that each step will take two and a half days with a probability of 80 percent. Does this mean that the entire project will take a week with the same probability of 80 percent? If you remember at least a little from the theory, then you have already answered that no, the probability will be completely different, except perhaps with the exception of especially exotic distributions, which usually do not occur in nature. <O: p> </ o: p>
See for yourself the example of, say, a normal distribution. The big blue vertical bar is the very project time that is achievable with an 80 percent probability. The picture shows the deviation back and forth by the same value t 0 , and the shaded areas show the probability of such a deviation, respectively. As you can see, the green area is much larger than pink, that is, it is much easier to fall behind for some fixed time than to overtake the project by the same fixed time. The fact is, I think no one is intuitively surprising, right?
<o: p>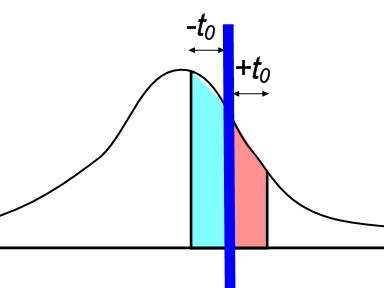
</ o: p>
For the most popular distribution for this kind of values ​​- Poisson, the picture will be the same. As in general, for the majority of distributions found in life. And this means that if you gave estimates of two project steps with a probability of 80 percent like t 1 and t 2 , then t 1 + t 2 will not be an estimate of the entire project with a probability of 80 percent. <O: p> </ o: p>
So as not to fool around with abstract problems, let's also take a look at the question a little more practical. Does it happen that a person finishes work ahead of time? Well, sometimes it happens, but as they say, a negligible value. After all, even if you finish earlier, most likely you are happily using the released time to clean the code, test it, make sure once again, right? Actually, everyday wisdom spread in collections devoted to the Murphy law simply says: “Any work takes all the time allotted to it.” <O: p> </ o: p>
With this amendment, everything becomes even more ridiculous. Since, if we accept that work less than planned does not take, then the project should still fit into t 1 + t 2 , so that both tasks are completed during the planned time, which, I recall, was estimated with a probability of 80 percent. Now it's time to pull out the school textbook on mathematics and count what the probability of the whole project is to keep within the time counted in the Project or else as an addition: <o: p> </ o: p>
P (T1 & T2) = P (T1) * P (T2) = 0.8 * 0.8 = 0.64 <o: p> </ o: p>
That is, if you broke the project into two parts, estimated each with 80 percent probability, then the sum has “reliability” of only 64 percent! Try as homework, what happens if the project is divided into ten steps? Have tried? Yeah. Just over ten percent. Even if you quantify 90 percent of each step from engineers, the chances of your ten-step project will be only 35 percent. <O: p> </ o: p>
By the way, this is why Joel Spolsky, in his Evidence Based Scheduling ( http://www.joelonsoftware.com/items/2007/10/26.html ), insists that the estimates should not be added, but received from the estimates of the steps by the Monte Carlo method . <o: p> </ o: p>
Of course, it can be noted that the quality of individual assessments greatly influences the quality of the assessment of the whole. So an improvement in the assessment of steps from 80 to 90 percent improved the evaluation of the project from ten steps from 10 to 35 percent. But let's be honest, and 35 percent will suit you? And how often do you do projects from just ten steps? And with a hundred steps, even very high-quality step estimates with 99 percent probability for each step will give you at the end less than 40 percent chance for the entire project. Are you satisfied with 40 percent? And where will you find engineers who make mistakes only once out of a hundred and at the same time not devoting all day to writing a single comment line? <O: p> </ o: p>
Of course, in fairness it should be noted that such a "collapse" of the chances of success occurs only for steps on the critical path. But do not forget that if you use your resources (people) efficiently, even with a sufficiently small delay, any step may be on a critical path. So the situation may not be as bad as in the examples above, but not as good as we would like. However, you know that too ...: -) <o: p> </ o: p>
Of course, now there will be a natural question, but what to do? You know, something is possible. But this is a subject for a separate article, and not one. <O: p> </ o: p>
And completely dotting the “i”, briefly, what I was trying to say in this article: <o: p> </ o: p>
1. Evaluation is not when the project is done. This is the time at which he will meet with a given probability . Even if the manager or engineer does not know this, it is still there and depends on the optimism of the engineer and the manager’s aggressiveness towards the lagging behind. <O: p> </ o: p>
2. Management introduces an order of magnitude larger errors in project evaluations, adding estimates of individual steps, rather than engineers, evaluating these individual steps. <O: p> </ o: p>
3. Even small errors in the estimates of individual steps can significantly reduce the reliability of the assessment of the entire project. <O: p> </ o: p>
4. And as usual, the calculator does not replace the brain, and Microsoft Project - the art of management. <O: p> </ o: p>
5. Oh, yes, one more thing: Do not make yourself an idol. Including from fashionable techniques. <O: p> </ o: p>
<o: p> </ o: p>
In this article, I'm going to talk about things that you all have known for a long time. Now I suggest to think about them. <? Xml: namespace prefix = o ns = "urn: schemas-microsoft-com: office: office" /> <o: p> </ o: p>
If you are not new to the software industry, then you are aware that from time to time, any manager finds himself in a phase when he becomes sharply interested in estimating time, work ... And usually, not by any means, but by some fashionable technique. You are asked to report in a week how long the bugs and the feature, which design has not yet managed to do, will take, not to mention the fact that the planned work certainly should be broken into pieces up to an hour, if you can’t be done every minute. .. <o: p> </ o: p>
How is time usually estimated for projects? Everyone knows that it’s impossible to estimate a large piece correctly, so it is broken up into smaller pieces, and then these smaller pieces are put together, for example, in some Gantt diagram or just on a calendar or Excel. <O: p> < / o: p>
')
Today I would like to talk about two completely wrong assumptions that underlie this technique. <O: p> </ o: p>
To begin with, what is the estimated time of the project or is there a project step? <O: p> </ o: p>
No, no, I understand that in the expectations of management, you, like Cassandra, must absolutely predict the future, and unlike Cassandra, this is not an example more optimistic, as business tenets demand (I don’t know how this thing translates, something like a moral code of a young builder of communism - we have to have training for it every year). In general, everyone understands that it is difficult, but your prophecies should be “good enough!” From all points of view. <O: p> </ o: p>
Well, when managers say so - this is understandable. But we are not managers, we are engineers, techies. We know that “good enough” is something very vague. And to be part of an engineering discipline, a concept must be measurable in numbers. That is, I want to somehow measure this matter in order to say distinctly “good enough” or still not “good enough”. And when an engineer wants to measure something, he applies such harmful science - mathematics. It’s harmful because it constantly talks about managers about what it thinks of them, and it’s also right ... <o: p> </ o: p>
So, what is the evaluation in mathematics, more precisely in the statistics and probability theory. And this is the interval in which the expected random variable with a given probability falls. A random variable is how long a project will take or there will be a separate project step. It seems that what is necessary, what the doctor prescribed, that's just what to do with a given probability? <O: p> </ o: p>
Try to approach the manager and say, “With a probability of 80 percent, this project will meet a month.” What will he tell you?
Yeah, have you already felt a slight indisposition? Further better. He wants “for sure”, but what does the mathematics say to this? Imagine a picture of some familiar distribution, say, a Poisson or normal Gaussian. What is the interval, the probability of falling into which is 100 percent? That's right, alas, if the manager wants a guaranteed estimate, then mathematically it is always infinity. Well, or practically, the period for which the project is simply beaten. Any project has a chance of failure. Good engineers, who were allowed to make good grades, have less chance of failure, and bad ones have much more, but still, under no circumstances, it is not zero. <O: p> </ o: p>
That is, volens-nolens will take off your estimates, which will be considered as your promise, although in reality they will be estimates for a probability of eighty, ninety, ninety-five percent ... <o: p> </ o: p>
So, the evaluation of a project or a project step is the time interval in which it will be packed with a probability that is comfortable for you. Or you can say with a comfortable risk for you not to meet. <O: p> </ o: p>
Suppose you choose 80 percent as such (respectively, the risk does not meet the 20 percent). Yes, I know, it sounds very risky, but watching programmers on natural conditions I had the feeling that even 80 percent for the majority are excessively high. Normally, smart managers multiply developer ratings at least one and a half to two times. <O: p> </ o: p>
So, you have a project, it has two steps. You estimate that each step will take two and a half days with a probability of 80 percent. Does this mean that the entire project will take a week with the same probability of 80 percent? If you remember at least a little from the theory, then you have already answered that no, the probability will be completely different, except perhaps with the exception of especially exotic distributions, which usually do not occur in nature. <O: p> </ o: p>
See for yourself the example of, say, a normal distribution. The big blue vertical bar is the very project time that is achievable with an 80 percent probability. The picture shows the deviation back and forth by the same value t 0 , and the shaded areas show the probability of such a deviation, respectively. As you can see, the green area is much larger than pink, that is, it is much easier to fall behind for some fixed time than to overtake the project by the same fixed time. The fact is, I think no one is intuitively surprising, right?
<o: p>
</ o: p>For the most popular distribution for this kind of values ​​- Poisson, the picture will be the same. As in general, for the majority of distributions found in life. And this means that if you gave estimates of two project steps with a probability of 80 percent like t 1 and t 2 , then t 1 + t 2 will not be an estimate of the entire project with a probability of 80 percent. <O: p> </ o: p>
So as not to fool around with abstract problems, let's also take a look at the question a little more practical. Does it happen that a person finishes work ahead of time? Well, sometimes it happens, but as they say, a negligible value. After all, even if you finish earlier, most likely you are happily using the released time to clean the code, test it, make sure once again, right? Actually, everyday wisdom spread in collections devoted to the Murphy law simply says: “Any work takes all the time allotted to it.” <O: p> </ o: p>
With this amendment, everything becomes even more ridiculous. Since, if we accept that work less than planned does not take, then the project should still fit into t 1 + t 2 , so that both tasks are completed during the planned time, which, I recall, was estimated with a probability of 80 percent. Now it's time to pull out the school textbook on mathematics and count what the probability of the whole project is to keep within the time counted in the Project or else as an addition: <o: p> </ o: p>
P (T1 & T2) = P (T1) * P (T2) = 0.8 * 0.8 = 0.64 <o: p> </ o: p>
That is, if you broke the project into two parts, estimated each with 80 percent probability, then the sum has “reliability” of only 64 percent! Try as homework, what happens if the project is divided into ten steps? Have tried? Yeah. Just over ten percent. Even if you quantify 90 percent of each step from engineers, the chances of your ten-step project will be only 35 percent. <O: p> </ o: p>
By the way, this is why Joel Spolsky, in his Evidence Based Scheduling ( http://www.joelonsoftware.com/items/2007/10/26.html ), insists that the estimates should not be added, but received from the estimates of the steps by the Monte Carlo method . <o: p> </ o: p>
Of course, it can be noted that the quality of individual assessments greatly influences the quality of the assessment of the whole. So an improvement in the assessment of steps from 80 to 90 percent improved the evaluation of the project from ten steps from 10 to 35 percent. But let's be honest, and 35 percent will suit you? And how often do you do projects from just ten steps? And with a hundred steps, even very high-quality step estimates with 99 percent probability for each step will give you at the end less than 40 percent chance for the entire project. Are you satisfied with 40 percent? And where will you find engineers who make mistakes only once out of a hundred and at the same time not devoting all day to writing a single comment line? <O: p> </ o: p>
Of course, in fairness it should be noted that such a "collapse" of the chances of success occurs only for steps on the critical path. But do not forget that if you use your resources (people) efficiently, even with a sufficiently small delay, any step may be on a critical path. So the situation may not be as bad as in the examples above, but not as good as we would like. However, you know that too ...: -) <o: p> </ o: p>
Of course, now there will be a natural question, but what to do? You know, something is possible. But this is a subject for a separate article, and not one. <O: p> </ o: p>
And completely dotting the “i”, briefly, what I was trying to say in this article: <o: p> </ o: p>
1. Evaluation is not when the project is done. This is the time at which he will meet with a given probability . Even if the manager or engineer does not know this, it is still there and depends on the optimism of the engineer and the manager’s aggressiveness towards the lagging behind. <O: p> </ o: p>
2. Management introduces an order of magnitude larger errors in project evaluations, adding estimates of individual steps, rather than engineers, evaluating these individual steps. <O: p> </ o: p>
3. Even small errors in the estimates of individual steps can significantly reduce the reliability of the assessment of the entire project. <O: p> </ o: p>
4. And as usual, the calculator does not replace the brain, and Microsoft Project - the art of management. <O: p> </ o: p>
5. Oh, yes, one more thing: Do not make yourself an idol. Including from fashionable techniques. <O: p> </ o: p>
<o: p> </ o: p>
Source: https://habr.com/ru/post/16179/
All Articles