We forge your signature with the help of a hinge mechanism. Kempe theorem
In this post I will tell you about the program that forges any signature with the help of a hinge mechanism. The program is based on the Kempe theorem, proved in the middle of the 19th century.
With the development of technology and the emergence of trains, inquisitive minds have a very interesting problem, and whether it is possible to create a hinge mechanism that translates a circular motion into movement in a straight line, to put it differently, draws a straight line. The hinge mechanism is a lot of sticks fastened together, which can freely rotate at the points of attachment. Many scientists struggled with this problem, inventing ingenious mechanisms, but they all drew inaccurate lines. For example, the mechanisms of Watt, Chebyshev and Hoiken:
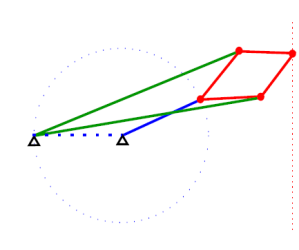
Many mathematicians believed that the problem of creating a hinge mechanism, which draws an ideal straight line, is basically unsolvable, until in the middle of the 19th century the ingenious Lipkin-Posselye mechanism was discovered, which paints an exact straight line:
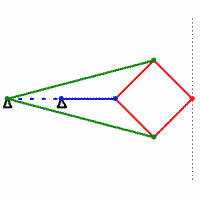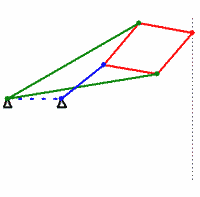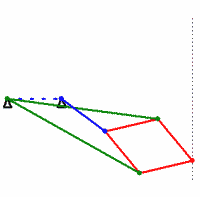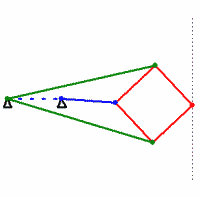
In this mechanism, all the sticks of the same color have the same length. Prove that the mechanism actually draws a straight line can be direct calculations, as they say, in the forehead. But people familiar with the inversion transform can see a fairly clear logic in the proof . By the time of the invention of the Lipkin-Posselier mechanism, the lubricants were already so good that they could do without this ideal converter into straight-line motion in engineering. After all, it is possible through another wand to transmit an almost straight motion to the piston. This stick will not always be perfectly parallel to the piston guide, but there is nothing wrong with that. As a result, the Lipkin-Posselier mechanism did not find wide application in engineering, but it had a huge impact on mathematics.
A few years later, Kempe, a mathematician-lawyer, gives an algorithm, how absolutely for any algebraic curve on a plane to build a hinge mechanism that can only draw this curve and cannot do anything else. In other words, there is a mechanism that is limited in movement by one degree of freedom. Moving along this degree of freedom, the mechanism draws our algebraic curve. Excellent presentation of evidence Kempe I found in this article . We remind the reader that the algebraic curves referred to in the Kempe theorem are the curves given by the equation where
where  - any polynomial. For example,
- any polynomial. For example,  Is a circle of radius
Is a circle of radius  ,
, 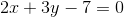 - the inclined straight line
- the inclined straight line 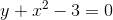 - parabola. In his proof, Kempe uses many interesting ideas, but the Lipkin-Posselier mechanism already known to us is a key building tool.
- parabola. In his proof, Kempe uses many interesting ideas, but the Lipkin-Posselier mechanism already known to us is a key building tool.
As soon as I learned about the Kempe theorem, I immediately wanted to write a program in which the user can draw any curve, say his signature, and the program approximates the signature of an algebraic curve, and then Kempe will construct a hinge mechanism that falsifies it. I really wanted to make a web application so that the user does not need to install anything on the computer, so that you can go to the site and run everything “in one click”. Since I am not a programmer, it was still a great opportunity for me to get acquainted with JavaScript and HTML5.
After I learned the evidence from Kempe, I had a very serious problem:
how to approximate the signature of an algebraic curve with good accuracy, fast, and even slow javascript? There is a very simple, but unsuitable way for us to approximate a curve by combining small circles scattered along the curve, as shown in the picture:
with good accuracy, fast, and even slow javascript? There is a very simple, but unsuitable way for us to approximate a curve by combining small circles scattered along the curve, as shown in the picture:

Every little The second circle is obviously an algebraic curve, since it is given by a polynomial equation
The second circle is obviously an algebraic curve, since it is given by a polynomial equation 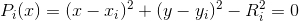 where
where  - the center of the circle, and
- the center of the circle, and 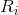 - its radius. The algebraic curve, obviously, will be the union of all small circles, since this union will be given by a polynomial equation
- its radius. The algebraic curve, obviously, will be the union of all small circles, since this union will be given by a polynomial equation  . But as you see, this kind of approximation doesn’t suit us at all, because there are so many self-intersection points. I would like to have a more "beautiful" approximation. It turns out that the problem of “beautiful” approximation is difficult both from a mathematical point of view and from a computational one. To somehow feel this, it is useful to present an algebraic curve.
. But as you see, this kind of approximation doesn’t suit us at all, because there are so many self-intersection points. I would like to have a more "beautiful" approximation. It turns out that the problem of “beautiful” approximation is difficult both from a mathematical point of view and from a computational one. To somehow feel this, it is useful to present an algebraic curve.  as the intersection of the surface
as the intersection of the surface  and planes
and planes 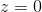 . The intersection line is very sensitive to the coefficients of a polynomial.
. The intersection line is very sensitive to the coefficients of a polynomial.  it can be completely uncontrollable, incoherent, have branch points, which will spoil the "beauty" of the approximation.
it can be completely uncontrollable, incoherent, have branch points, which will spoil the "beauty" of the approximation.
After a week of experimenting with various algorithms, all my attempts to somehow approximate the curve turned out to be in vain. All algorithms worked very slowly and poorly. I almost gave up, having previously posted a question on mathoverflow , where many professional mathematicians traditionally sit. In the question I casually mentioned that I need it in order to forge signatures with hinges. What was my surprise that in a day or two I was answered by the mathematician Mikhail Kapovich . He replied "not in the eyebrow, but in the eye." As it turned out, he once studied the Kempe theorem and, together with John Millson, proved in his article that it is possible to construct hinge mechanisms not only for algebraic curves, but also for curves that are more naturally suitable for approximation problems, namely, for curves given parametrically with polynomial expressions:
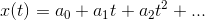
')
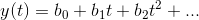
With such curves it is easier to approximate any continuous curves, including our signature. You can approximate the so-called Chebyshev polynomials , and you can first approximate the Fourier series, and then trigonometric functions in the Fourier series approximate the Taylor series. It turns out that instead of trying to approximate a curve with algebraic curves, it is better to change Kempe’s proof itself and learn how to construct hinged mechanisms that can construct curves that are more suitable for approximation problems.
The whole story felt like a huge diamond find. But, to my shame, I did not fully understand that article. The article is written quite difficult. But the fact that there is a solution to my problem opened my eyes. I realized that a slight change in the original Kempe proof can be used to build hinges that draw cosine trigonometric curves, that is, curves of the form
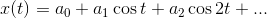

With such curves it is even easier to approximate our signature (the theory of Fourier series) than with curves from the article by Kapovich-Millson. Indeed, it follows from the theory of Fourier series that on a segment functions
functions 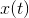 and
and 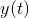 can be expanded in a row in cosines. For accuracy of approximation
can be expanded in a row in cosines. For accuracy of approximation 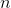 we have:
we have:

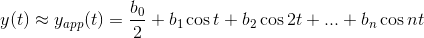
Coefficients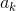 and
and  easy to find. You just need to multiply the equalities left and right
easy to find. You just need to multiply the equalities left and right  and integrate from
and integrate from  before
before 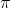 , then in the right part almost all the integrals will be reset to zero, except for one at the term
, then in the right part almost all the integrals will be reset to zero, except for one at the term 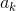 in the first equality and with a member
in the first equality and with a member  in the second. The result will be:
in the second. The result will be:
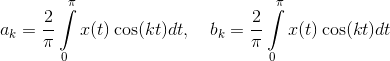
I thought for a very long time whether to post in this post an algorithm for constructing hinges that build these trigonometric curves. Then I realized that it would add mathematical dullness to the text. People usually do not like to read long proofs in texts of this kind. Therefore, I will manage just a link (upd: mirror ). Curious can look.
And here, in fact, the application itself, which forges your signature: david.wf/linkage . (upd: mirror ) Please note, you can use the mouse to move the structure, and the scroller to zoom in and out (upd: the degree of approximation can also be changed with a special slider “approximation”). The application works on modern browsers, I have not tested the old ones. The least slows down on chrome, since only chrome is much faster than other browsers draws straight ( pruflink ). Frankly, I spent a lot of effort on optimization, so that nothing slowed down on weak computers, but, to be honest, I didn’t achieve much success. Once again, the hinge that the program builds is not able to draw anything except your signature. The hinge is driven by a spinning blue triangle - the “engine”.

Kempe theorem
With the development of technology and the emergence of trains, inquisitive minds have a very interesting problem, and whether it is possible to create a hinge mechanism that translates a circular motion into movement in a straight line, to put it differently, draws a straight line. The hinge mechanism is a lot of sticks fastened together, which can freely rotate at the points of attachment. Many scientists struggled with this problem, inventing ingenious mechanisms, but they all drew inaccurate lines. For example, the mechanisms of Watt, Chebyshev and Hoiken:
 |  |  |
Many mathematicians believed that the problem of creating a hinge mechanism, which draws an ideal straight line, is basically unsolvable, until in the middle of the 19th century the ingenious Lipkin-Posselye mechanism was discovered, which paints an exact straight line:

In this mechanism, all the sticks of the same color have the same length. Prove that the mechanism actually draws a straight line can be direct calculations, as they say, in the forehead. But people familiar with the inversion transform can see a fairly clear logic in the proof . By the time of the invention of the Lipkin-Posselier mechanism, the lubricants were already so good that they could do without this ideal converter into straight-line motion in engineering. After all, it is possible through another wand to transmit an almost straight motion to the piston. This stick will not always be perfectly parallel to the piston guide, but there is nothing wrong with that. As a result, the Lipkin-Posselier mechanism did not find wide application in engineering, but it had a huge impact on mathematics.
A few years later, Kempe, a mathematician-lawyer, gives an algorithm, how absolutely for any algebraic curve on a plane to build a hinge mechanism that can only draw this curve and cannot do anything else. In other words, there is a mechanism that is limited in movement by one degree of freedom. Moving along this degree of freedom, the mechanism draws our algebraic curve. Excellent presentation of evidence Kempe I found in this article . We remind the reader that the algebraic curves referred to in the Kempe theorem are the curves given by the equation
Process
As soon as I learned about the Kempe theorem, I immediately wanted to write a program in which the user can draw any curve, say his signature, and the program approximates the signature of an algebraic curve, and then Kempe will construct a hinge mechanism that falsifies it. I really wanted to make a web application so that the user does not need to install anything on the computer, so that you can go to the site and run everything “in one click”. Since I am not a programmer, it was still a great opportunity for me to get acquainted with JavaScript and HTML5.
After I learned the evidence from Kempe, I had a very serious problem:
how to approximate the signature of an algebraic curve

Every little
After a week of experimenting with various algorithms, all my attempts to somehow approximate the curve turned out to be in vain. All algorithms worked very slowly and poorly. I almost gave up, having previously posted a question on mathoverflow , where many professional mathematicians traditionally sit. In the question I casually mentioned that I need it in order to forge signatures with hinges. What was my surprise that in a day or two I was answered by the mathematician Mikhail Kapovich . He replied "not in the eyebrow, but in the eye." As it turned out, he once studied the Kempe theorem and, together with John Millson, proved in his article that it is possible to construct hinge mechanisms not only for algebraic curves, but also for curves that are more naturally suitable for approximation problems, namely, for curves given parametrically with polynomial expressions:
')
With such curves it is easier to approximate any continuous curves, including our signature. You can approximate the so-called Chebyshev polynomials , and you can first approximate the Fourier series, and then trigonometric functions in the Fourier series approximate the Taylor series. It turns out that instead of trying to approximate a curve with algebraic curves, it is better to change Kempe’s proof itself and learn how to construct hinged mechanisms that can construct curves that are more suitable for approximation problems.
The whole story felt like a huge diamond find. But, to my shame, I did not fully understand that article. The article is written quite difficult. But the fact that there is a solution to my problem opened my eyes. I realized that a slight change in the original Kempe proof can be used to build hinges that draw cosine trigonometric curves, that is, curves of the form
With such curves it is even easier to approximate our signature (the theory of Fourier series) than with curves from the article by Kapovich-Millson. Indeed, it follows from the theory of Fourier series that on a segment
Coefficients
I thought for a very long time whether to post in this post an algorithm for constructing hinges that build these trigonometric curves. Then I realized that it would add mathematical dullness to the text. People usually do not like to read long proofs in texts of this kind. Therefore, I will manage just a link (upd: mirror ). Curious can look.
And here, in fact, the application itself, which forges your signature: david.wf/linkage . (upd: mirror ) Please note, you can use the mouse to move the structure, and the scroller to zoom in and out (upd: the degree of approximation can also be changed with a special slider “approximation”). The application works on modern browsers, I have not tested the old ones. The least slows down on chrome, since only chrome is much faster than other browsers draws straight ( pruflink ). Frankly, I spent a lot of effort on optimization, so that nothing slowed down on weak computers, but, to be honest, I didn’t achieve much success. Once again, the hinge that the program builds is not able to draw anything except your signature. The hinge is driven by a spinning blue triangle - the “engine”.
Source: https://habr.com/ru/post/161301/
All Articles