Simplest triangulation in java
Good day to all!
I want to talk about one interesting problem and its solution, which I applied in one of my projects.
The essence of the problem is as follows:
There are several signal detectors (for example, GSM base stations). And these detectors send to the server the signal level for a certain source. It is necessary to calculate and display on the map the coordinates of the source
If you are interested in how to do this, welcome under cat.
Let A (xa, ya), B (xb, yb), C (xc, yc) be signal detectors with given coordinates in a certain rectangular coordinate system. O (xo, yo) - signal source.
We recall from the school textbook of physics that the amplitude of the signal is inversely proportional to the square of the distance to the source. Thus, the distance Ra from the source O to the detector A will be equal to
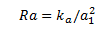
where ka is some coefficient that we can get when calibrating devices.
The formula for calculating the distance a1 is taken from the school course of geometry (it is embarrassing to give it here, but let it be for completeness).
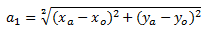
The heterogeneity of the environment is neglected. Yes, it will give some error, but the solution to this problem is beyond the scope of the problem. We assume that the constant factors affecting the propagation of the signal (the presence and material of the walls, for example) are already embedded in the coefficient ka. Temporary factors - interference, signal re-reflection, etc. - will affect the result, but in practice, even indoors they do not interfere very much.
Thus, we have dependency formulas for distance from all sources.
If we solve the problem "in the forehead" - we have a system of quadratic equations, the solution of which will give us a point with coordinates xo, yo. The problem is that the university course of linear algebra I forgot a little. After a week of thinking, I stumbled upon this method.
Let's draw around each detector a circle whose radius is inversely proportional to the signal level. The area of intersection of all circles and will contain the signal source. For simplicity, we can assume that the source is in the center of this area.
We build a drawing for a case with three detectors and one source.
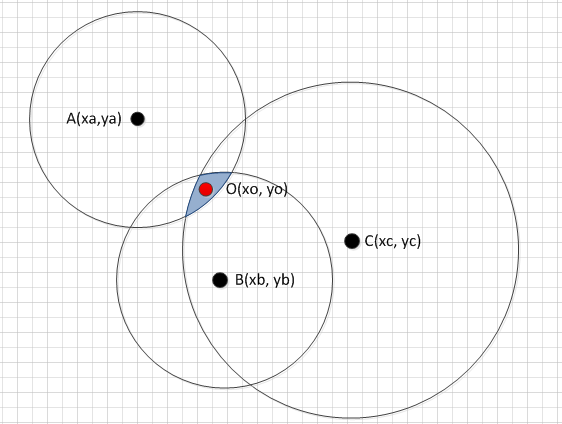
Here B and A are closest to the signal source, so the diameter of the circle is smaller. C farthest, diameter larger. The dependence of the diameter of the circle on the signal level is determined experimentally. This drawing is built in real coordinates (say, meters), in order to go to practice, we translate them into pixels in the most usual way. You just need to know the size of the map (width, height) in pixels and in meters. The nonlinearity of the projection (if it is a satellite image) is as before neglected. It is better to use a large-scale scheme, in my project it was a floor plan.
So, a simple solution is found, we will try to put it into practice. The server part of my project was developed in Java, receives data from TCP detectors with SSL encryption in json format. This part of the code is independent, it is executed in a separate thread. Received events are stored in the mysql database.
Triangulation works in its stream, selects events that have not yet been processed from the mysql database (no later than 3 seconds before the current time - in order to receive information about the same signal from all sources).
Although the solution turned out to be simple and does not require any mathematics, it is also somehow necessary to short-cut the intersection of the circles. Fortunately, Java has an AWT library that will do everything for us. The absence of the window interface does not confuse her, and some of its classes work fine on the server in the backend.
I cite a bit simplified code from the project.
So, as you understand, ppx / ppy are coefficients for converting real coordinates to pixels.
We take the signal level for the first detector, calculate the distance to the source, build a circle using coordinates known to us with the obtained radius.
Now we go through all the remaining sources and do the same. We intersect the first circle with the result; we use the result in the cycle for the remaining detectors. An additional trick - we intersect with the rectangle of the room, otherwise it may happen that the result will go beyond it, that we do not need.
Well, in the end we check that we have at least something left as a result, plus we calculate the calculation error (like half the diagonal of the rectangle in which the resulting area is inscribed).
This is the function to calculate the distance.
Previously, it was a logarithmic function, but, unfortunately, the attenuation of a real signal is different, we had to look at the signal level at several points in the laboratory and record the signal level and the corresponding distance in two arrays.
I removed the real numbers just in case so as not to disturb the NDA.
By the way, absolutely the same solution is possible on C #. Instead of Area, you need to use GraphicsPath, there is an Intersect method. The only difficulty is finding the center of the intersection obtained. Here is the code to find the center of the region in C #:
So, not having sufficient knowledge in mathematics and physics, with certain assumptions, it is possible to solve a rather complicated problem.
Thanks for attention!
I want to talk about one interesting problem and its solution, which I applied in one of my projects.
The essence of the problem is as follows:
There are several signal detectors (for example, GSM base stations). And these detectors send to the server the signal level for a certain source. It is necessary to calculate and display on the map the coordinates of the source
If you are interested in how to do this, welcome under cat.
Part 1. Theory and some geometry
Let A (xa, ya), B (xb, yb), C (xc, yc) be signal detectors with given coordinates in a certain rectangular coordinate system. O (xo, yo) - signal source.
We recall from the school textbook of physics that the amplitude of the signal is inversely proportional to the square of the distance to the source. Thus, the distance Ra from the source O to the detector A will be equal to
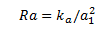
where ka is some coefficient that we can get when calibrating devices.
The formula for calculating the distance a1 is taken from the school course of geometry (it is embarrassing to give it here, but let it be for completeness).
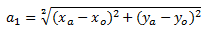
The heterogeneity of the environment is neglected. Yes, it will give some error, but the solution to this problem is beyond the scope of the problem. We assume that the constant factors affecting the propagation of the signal (the presence and material of the walls, for example) are already embedded in the coefficient ka. Temporary factors - interference, signal re-reflection, etc. - will affect the result, but in practice, even indoors they do not interfere very much.
Thus, we have dependency formulas for distance from all sources.
If we solve the problem "in the forehead" - we have a system of quadratic equations, the solution of which will give us a point with coordinates xo, yo. The problem is that the university course of linear algebra I forgot a little. After a week of thinking, I stumbled upon this method.
Let's draw around each detector a circle whose radius is inversely proportional to the signal level. The area of intersection of all circles and will contain the signal source. For simplicity, we can assume that the source is in the center of this area.
We build a drawing for a case with three detectors and one source.

Here B and A are closest to the signal source, so the diameter of the circle is smaller. C farthest, diameter larger. The dependence of the diameter of the circle on the signal level is determined experimentally. This drawing is built in real coordinates (say, meters), in order to go to practice, we translate them into pixels in the most usual way. You just need to know the size of the map (width, height) in pixels and in meters. The nonlinearity of the projection (if it is a satellite image) is as before neglected. It is better to use a large-scale scheme, in my project it was a floor plan.
Part 2. We proceed to practice.
So, a simple solution is found, we will try to put it into practice. The server part of my project was developed in Java, receives data from TCP detectors with SSL encryption in json format. This part of the code is independent, it is executed in a separate thread. Received events are stored in the mysql database.
Triangulation works in its stream, selects events that have not yet been processed from the mysql database (no later than 3 seconds before the current time - in order to receive information about the same signal from all sources).
Although the solution turned out to be simple and does not require any mathematics, it is also somehow necessary to short-cut the intersection of the circles. Fortunately, Java has an AWT library that will do everything for us. The absence of the window interface does not confuse her, and some of its classes work fine on the server in the backend.
I cite a bit simplified code from the project.
public static TriangulationPoint triangulate(AlertDbo sourceAlert, AlertDbo[] children, MapFileDbo map) { … double ppx = map.getWidth() / map.getRealWidth(); //pixels per feet horizontal double ppy = map.getHeight() / map.getRealHeight(); //pixels per feet vertical So, as you understand, ppx / ppy are coefficients for converting real coordinates to pixels.
We take the signal level for the first detector, calculate the distance to the source, build a circle using coordinates known to us with the obtained radius.
double strength = sourceAlert.getSignalStrength(); double distance = calculateDistance(strength *sourceAlert.getDetector().getKoef()); MapCoordDbo coord = sourceAlert.getCoords(); … Area area = new Area(new Ellipse2D.Double(coord.getX(), coord.getY(), distance*2, distance*2)); Now we go through all the remaining sources and do the same. We intersect the first circle with the result; we use the result in the cycle for the remaining detectors. An additional trick - we intersect with the rectangle of the room, otherwise it may happen that the result will go beyond it, that we do not need.
for(int j=0;j<children.length;j++) { … strength = children[j].getSignalStrength(); distance = calculateDistance(strength * children[j].getDetector().getKoef()); coord = children[j].getCoords(); area.intersect(new Area( new Ellipse2D.Double(coord.getX(), coord.getY(), distance*2, distance*2) )); area.intersect(new Area(new Rectangle(0, 0, map.getWidth(), map.getHeight()))); } Well, in the end we check that we have at least something left as a result, plus we calculate the calculation error (like half the diagonal of the rectangle in which the resulting area is inscribed).
if(area.getBounds().getWidth()>0 && area.getBounds().getHeight()>0) { TriangulationPoint tp = new TriangulationPoint(); tp.x = area.getBounds().getCenterX(); tp.y = area.getBounds().getCenterY(); double dx = area.getBounds().getWidth() / 2; double dy = area.getBounds().getHeight() / 2; tp.err = Math.sqrt(dx*dx + dy*dy) /2; return tp; } return null; } This is the function to calculate the distance.
public static double calculateDistance(double db) { double[] dbs = {…}; double[] fts = {…}; double koef = -…; double prevDb = 70; double prevDist = 0; for(int i=0;i<dbs.length;i++) { if(dbs[i]<db) { break; } koef = (dbs[i] - prevDb) / (fts[i] - prevDist); prevDb = dbs[i]; prevDist = fts[i]; } return prevDist + koef * (db - prevDb); } Previously, it was a logarithmic function, but, unfortunately, the attenuation of a real signal is different, we had to look at the signal level at several points in the laboratory and record the signal level and the corresponding distance in two arrays.
I removed the real numbers just in case so as not to disturb the NDA.
By the way, absolutely the same solution is possible on C #. Instead of Area, you need to use GraphicsPath, there is an Intersect method. The only difficulty is finding the center of the intersection obtained. Here is the code to find the center of the region in C #:
private PointF RegionCentroid(Region region, Matrix transform) { float mx = 0; float my = 0; float total_weight = 0; foreach (RectangleF rect in region.GetRegionScans(transform)) { float rect_weight = rect.Width * rect.Height; mx += rect_weight * (rect.Left + rect.Width / 2f); my += rect_weight * (rect.Top + rect.Height / 2f); total_weight += rect_weight; } return new PointF(mx / total_weight, my / total_weight); } So, not having sufficient knowledge in mathematics and physics, with certain assumptions, it is possible to solve a rather complicated problem.
Thanks for attention!
')
Source: https://habr.com/ru/post/161195/
All Articles