About two-dimensional packaging: online algorithms
This is a continuation of the post about offline packaging algorithms.The essence of the problem: we have a semi-infinite strip - as in tetris, only without a game over, and a finite set of rectangles. Rectangle data comes in real time; Each new rectangle must be placed immediately and no longer move. The goal is to minimize the overall height of the packed rectangles.
This is an online variation of the problem of packing rectangles into a semi-bounded strip (2 Dimensional Strip Packing, 2DSP).
A little more theoretical information can be found in the previous article, but for now, without further ado, let's turn to the algorithms.
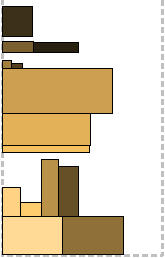
For illustration, this sequence of bricks will be used:
(The source data sponsor is random.org).
Some heuristic algorithms will be described, the general idea of which is to pre-divide a strip into areas and place newly incoming rectangles in a specific area according to certain criteria.
')
Level algorithms
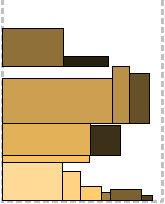
The approach of all level algorithms is that the strip is divided into levels, based on the height of the rectangles present at this stage. Rectangles are placed along the bottom of the current level from left to right as long as possible; a rectangle that does not fit is packed to the next level. The height of each level is determined by the highest rectangle in it. Here are three packaging options:
Next Fit Level - when the next level opens, the previous one “closes” and is no longer considered;
First Fit Level - at each step of the algorithm, each level is viewed, starting from the lowest one, and the rectangle is packed into the first suitable one, which has enough space;
Best Fit Level - at every step of the algorithm, all levels are viewed, and the most appropriate one is selected - the one at which there will be a minimum of space after packaging.
All three algorithms are illustrated above. At this stage, it is easy to guess which one.
Algorithms NFL, FFL, BFL
Next Fit Level
First Fit Level
Best Fit Level
Input: The dimensions of the rectangles {w (Li); h (Li)} and the strip width W.
Output: The height H and the packing.
1: level = 0; h (level + 1) = 0; H = 0; i = 0
2: while there is an unpacked rectangle do
3: i ++
4: if there is a level
5: pack rectangle left justified
6: if h (level + 1) <h (Li) then
7: h (level + 1) = h (Li)
8: end if
9: else [there is insufficient space on current level]
10: open the rectangle
11: H + = h (level + 1); level ++
12: end if
13: end while
14: print H and entire packing First Fit Level
Input: The dimensions of the rectangles {w (Li); h (Li)} and the strip width W.
Output: The height H and the packing.
1: level = 0; h (level + 1) = h (L1); H = h (L1); i = 1
2: while there is an unpacked rectangle do
3: i ++; level = 0
4: search for space level
5: if such a level exists then
6: pack rectangle left justified
7: if this is the level and h (level) <h (li) then
8: h (level) = h (Li)
9: end if
10: else [there is insufficient space in all existing levels]
11: create a new level above the top-most level
12: pack rectangle left justified
13: h (level) = h (Li); H + = h (Li)
14: end if
15: end while
16: print H and entire packing Best Fit Level
Input: The dimensions of the rectangles {w (Li); h (Li)} and the strip width W.
Output: The height H and the packing.
1: level = 0; h (level + 1) = h (L1); H = h (L1); i = 0
2: while there is an unpacked rectangle do
3: i ++; level = 0
4: Search for the lowest level with minimum residual horizontal space
5: if such a level exists then
6: pack rectangle left justified
7: else [such a level does not exist]
8: create a new level above the top-most level
9: pack rectangle left justified
10: h (level) = h (Li); H + = h (Li)
11: end if
12: end while
13: print H and entire packing Bi-Level Next Fit
Sly modification Next Fit Level. Levels are created in two, each with its own strategy.
The bottom level (or all odd ones): the first arriving rectangle is packed along the left edge, the rest - from right to left, while there is enough space. Then the level is closed and its height is determined by the highest rectangle in it.
Top level (or all even): if there is only one rectangle on the bottom level, the level is packed similarly to the bottom one. If two or more, then the first rectangle is packed over the lower of the two pressed to the edges of the strip, and also pressed against the edge of the strip; all subsequent ones are packed from right to left, regardless of whether the first one was packed - on the left or on the right.
It sounds confusing and not immediately clear why such dances with a tambourine. The only thing that this algorithm obviously provides is a more uniform distribution of rectangles over the volume of the strip, without skewing to the left edge. But we will return to this strategy when we consider compression algorithms.
BiNFL Algorithm
Bi-Level Next Fit
Input: The dimensions of the rectangles {w (Li); h (Li)} and the strip width W.
Output: The height H and the packing.
1: level = 1; h (level) = 0; H = 0; i = 1
2: open a new bi-level
3: call 'pack on lower level'
4: print H and entire packing
Procedure 'pack on lower level'
1: the first rectangle packed is left justified
2: subsequent rectangles that fit are right justified
3: if there is insufficient space then
4: h (level) tallest rectangle packed
5: call 'pack on upper level'
6: end if
Procedure 'pack on the upper level'
1: if Li + 1 is the first rectangle packed then
2: left justify on top of Li
3: else
4: if Li + 2 is the first rectangle packed then
5: pack above min {h (Li); h (Li + 1)}
6: justify according to min {h (Li); h (Li + 1)}
7: else
8: if Li + j (j> 3) fits on the upper level then
9: left justify all other rectangles
10: else [rectangle does not fit]
11: H + = h (lower) + h (upper); open new bi-level
12: end if
13: end if
14: end if Shelf algorithms
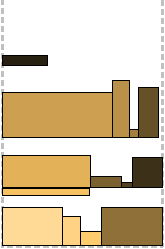
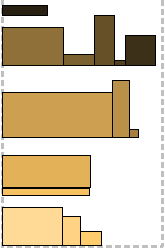
Shelf algorithms are not tied to the exact height of the rectangles, and after packing the first level (shelf) there is not much room left in case the next one is a little higher. This “little” is regulated by the parameter r ∈ (0; 1). The shelf height is defined as r k , where r k + 1 <h (L i ) ≤ r k for some integer k and the height of the first packed rectangle h (L i ). Similar to layered algorithms, Next Fit, First Fit, and Best Fit shelf bypass strategies are applied. The “reserve” left on each shelf becomes profitable in the last two cases (compare FFL and FFS, BFL and BFS). In the example, p = 0.7.
Algorithms NFS, FFS, BFS
Next Fit Shelf
First Fit Shelf
Best Fit Shelf
Input: The dimensions of the rectangles {w (Li); h (Li)}
w and strip width
Output: The height H and the packing.
1: shelf = 1; w (shelf) = 0;
h (shelf) = r ^ k for some integer k; i = 0; H = h (shelf)
2: while there is an unpacked rectangle do
3: i ++; compute k
4: if there is sufficient space and r ^ (k + 1) <h (Li) ≤ r ^ k then
5: Rectangle Packed Rectangle
6: else [there is insufficient space]
7: create one new shelf
Li and the pack.
8: shelf ++; H + = r ^ k
9: end if
10: end while
11: print H and entire packing. First Fit Shelf
Input: The dimensions of the rectangles {w (Li); h (Li)}
w and strip width
Output: The height H and the packing.
1: shelf = 1; h (shelf) = r ^ k for some integer k;
i = 0; H = h (shelf); shelfnum = 1
2: while there is an unpacked rectangle do
3: i ++; compute k
4: search for low height
5: if such a shelf exists then
6: Pack Rectangle Pack
7: else [there is insufficient space in all shelves of
appropriate height or such a shelf does not exist]
8: create a new shelf above the top-most shelf
Li and the pack.
9: shelf ++; H + = r ^ k; shelfnum ++
10: end if
11: end while
12: print H and entire packing. Best Fit Shelf
Input: The dimensions of the rectangles {w (Li); h (Li)}
w and strip width
Output: The height H and the packing.
1: shelf = 1; h (shelf) = r ^ k for some integer k;
i = 0; H = h (shelf); shelfnum = 1
2: while there is an unpacked rectangle do
3: i ++; compute k
4: search all shelves (starting with the bottom) for one
with appropriate height and has minimum horizontal space.
5: if such a shelf exists then
6: Pack Rectangle Pack
7: else [there is insufficient space or
there is no shelf of appropriate height]
8: create a new shelf above the top-most shelf
Li on the new shelf.
9: shelf ++; H + = r ^ k; shelfnum ++
10: end if
11: end while
12: print H and entire packing. Harmonic shelf
Harmonic Shelf packs rectangles one level not only with a similar height, but also with a similar width. The result will be more levels, but they will be filled with denser. An additional parameter M is introduced to calculate the allowable width.
The total width of the strip, for simplicity, we take it per unit, divided by M intervals I 1 .. I M. The author claims that a reasonable value of M is in [3; 12]. The width of the intervals is calculated by the formula:
; 
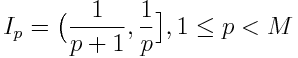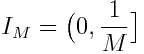
For each rectangle, p is calculated. Parameter k for height is calculated similarly to shelf algorithms. Two conditions are checked: is there a place on a shelf with height r k for a rectangle and does it correspond to p already packed there. If at least one is not done, it creates its own shelf, with blackjack and the most comfortable conditions. In the example, p = 0.7, M = 4.
HS Algorithm
Harmonic shelf
Input: The dimensions of the rectangles {w (Li); h (Li)}
the parameters M and the strip width W.
Output: The height H and the packing.
1: shelf = 1; h (shelf) = r ^ k for some integer k; i = 0
2: while there is an unpacked rectangle do
3: i ++; compute k such that r ^ (k + 1) <h (Li) ≤ r ^ k
4: compute the value of p such that 1 / (p + 1) <w (Li) ≤ 1 / p
where 1 ≤ p <M
5: amongst shelves of height r ^ k find the one
with packing rectangles
6: if there is a r ^ k then rectangle of height
7:
8: shelf ++
9: end if
10: if rectangle
11: h (shelf) = r ^ k; H + = h (shelf)
12: end if
13: end while
14: print H and entire packing Azar y
For division into levels, a certain threshold value 0 < Y <1/2 is introduced. The width of the rectangles is scaled according to the width of the strip, which is taken as one. Rectangles with a height of 2 j -1 <h (L i ) ≤ 2 j and a width of 2 - x -1 <h (L i ) ≤ 2 - x are packed into one level. That is, a level is characterized by a pair ( x , j ) for some integer j and natural x .
Rectangles with a width of at least Y are buffered and packed each on a separate level. That is, if you get such a rectangle, you urgently need to open a new level that is equal in height. All others (non-buffer) are packed at the first appropriate level. Suitable - in the sense of the same pair ( x , j ). If suddenly there is not enough space, a non-buffer rectangle may become the first in a new level, then the height of this level will be 2 j .
Some kind of unhealthy hierarchy, in general.
In the example, Y = 0.4.
Azar algorithm
Azar y
Input: The dimensions of the rectangles {w (Li); h (Li)}
the parameter Y and the strip width W.
Output: The height H and the packing.
1: h (level) = 0; w (level) = 0; level = 0
2: while there is an unpacked rectangle do
3: if w (Li) ≥ Y then
4: level ++; w (level) = w (Li); h (level) = h (Li); H + = h (level)
5: else [w (Li) <Y]
6: compute x and j such that
2 ^ (j-1) <h (Li) ≤ 2 ^ j and 2 ^ (- x-1) <w (Li) ≤ 2 ^ (- x)
7: search for the lowest (x, j) level
8: if no (x, j) level is available or Li is blocked then
9: level ++; h (level) = 2 ^ j; H + = h (level)
10: w (level) + = w (Li)
11: else [(x, j) level is available and not blocked]
12: w (level) + = w (Li)
13: end if
14: end if
15: end while
16: print H and entire packing Compression algorithms
Compression algorithms are based on BiNFL and are essentially patches to the top-level packaging method.
The general difference is that the top level is always packed from left to right.
Compression Part Fit: For each rectangle packed on the upper level, it is checked whether there is a space below it on the lower level. If it is possible to move it to the lower level so that a part of it remains at the upper level, it moves (from here Part Fit - it can be partially “pressed” into the previous level). In this way, the overall height of the second level can be reduced. More on the packaging, it does not radically affect. In the first picture you can see a rectangle hanging between the levels - it was shifted.
Compression Full Fit: For each rectangle packed to the top level, it is checked whether it can completely move down to the previous level. Actually, if it can, it shifts. This gives us a strategic advantage: the space thus freed up can be used for the next rectangle. Unfortunately, the second picture does not contain such a situation, but on it you can see two failed.
Compression Combo: Yes, yes, this is a combination of the two previous ones and, accordingly, a combination of their advantages. The third drawing illustrates.
Algorithms CPF, CFF, CC
Compression
Compression Part Fit
Compression Full Fit
Compression combo
Input: The dimensions of the rectangles {w (Li); h (Li)} and the strip width W.
Output: The height H and the packing.
1: i = 0; H = 0
2: open new bi-level
3: packing on lower level is similar to BiNFL; H + = h (lowerlevel)
4: if there is a gap
5: call 'pack on the upper level'
6: end if
7: print H and entire packing
Procedure 'pack on the upper level'
1: while there is an unpacked rectangle do
2: if i ≥ 3 and Li is the first rectangle packed then
3: justify according to the shorter
of the rectangles
4: slide rectangle downwards if there is a sufficient space
and go to 12
5: else
6: if i ≥ 3 and Li is the second rectangle packed then
7: right justify and go to 12
8: else [rectangle does not fit]
9: H + = h (upperlevel); open new bi-level
10: end if
11: end if
12: end while Compression Part Fit
Input: The dimensions of the rectangles {w (Li); h (Li)} and the strip width W.
Output: The height H and the packing.
1: i = 0; H = 0
2: open a new bi-level
3: packing on lower level is similar to BiNFL; H + = h (lowerlevel)
4: if there is a gap
5: call 'pack on the upper level'
6: end if
7: print H and entire packing
Procedure 'pack on the upper level'
1: while there is an unpacked rectangle do
2: if h (Li)> VerticalSpace and w (Li) ≤ HorizontalSpace then
3: shift rectangle Li downwards; go to 11
4: else
5: if h (Li) ≤ VerticalSpace and W - w (level) ≥ w (Li) then
6: left justify; go to 11
7: else [rectangle does not fit]
8: H + = h (upperlevel); open a new bi-level
9: end if
10: end if
11: end while Compression Full Fit
Input: The dimensions of the rectangles {w (Li); h (Li)} and the strip width W.
Output: The height H and the packing.
1: i = 0; H = 0
2: open a new bi-level
3: packing on lower level is similar to BiNFL; H + = h (lowerlevel)
4: if there is a gap
5: call 'pack on the upper level'
6: end if
7: print H and entire packing
Procedure 'pack on the upper level'
1: while there is an unpacked rectangle do
2: if h (Li) ≤ VerticalSpace and w (Li) ≤ HorizontalSpace then
3: slide rectangle Li downwards; go to 11
4: else
5: if h (Li) ≤ VerticalSpace and W - w (level) ≥ w (Li) then
6: left justify; go to 11
7: else [rectangle does not fit]
8: H + = h (upperlevel); open new bi-level
9: end if
10: end if
11: end while Compression combo
Input: The dimensions of the rectangles {w (Li); h (Li)} and the strip width W.
Output: The height H and the packing.
1: i = 0; H = 0
2: open a new bi-level
3: packing on lower level is similar to BiNFL; H + = h (lowerlevel)
4: if there is a gap
5: call 'pack on the upper level'
6: end if
7: print H and entire packing
Procedure 'pack on the upper level'
1: while there is an unpacked rectangle do
2: if w (Li) ≤ HorizontalSpace then
3: slide rectangle Li downwards; go to 11
4: else
5: if w (Li)> HorizontalSpace and W - w (level) ≥ w (Li) then
6: left justify, go to 11
7: else [rectangle does not fit]
8: H + = h (upperlevel); open new bi-level
9: end if
10: end if
11: end while Online fit
More time-consuming method than previous ones, but also more productive. Based on the Burke algorithm for an offline variant of the task. Some aspects I, perhaps, draw.
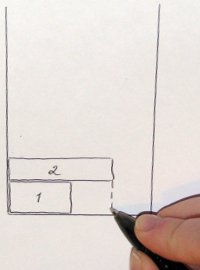
During the packaging, Empty Areas may form, which the algorithm will try to fill in first. How they can be formed can be seen in the photo on the left. Note that for this you need to store a certain representation of the fullness of the band.
After filling out from an empty area, it may turn out to be two (or it may not, you know).
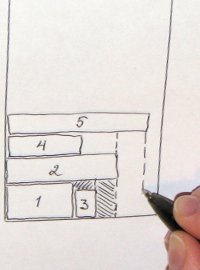
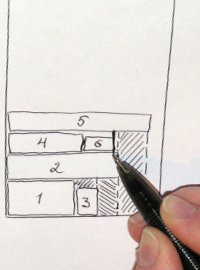Also, several areas can be created in one step at a time — the space below the rectangle is analyzed vertically and divided by the number of “steps”. On the middle photo, once again shows the division of the empty area into two after packing a rectangle there (by the way, it seems to me that in this place it would be better to split it horizontally ).In general, the farther into the forest, the more voids. At each step, the rapidly shallowing voids are closely examined. Here I see another optimization: you can enter a measure of appropriate area and discard unwanted ones.
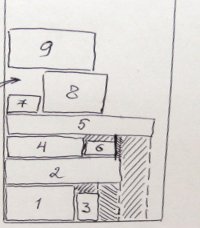If none of the empty areas match, the packaging continues with the Burke method. I remember. A height map for the strip is constructed, and the rectangle is tried on the lowest area at the moment. If he does not enter there, the low place is “filled” to the level of the nearest step, and the search is repeated. So a potential place can be pushed to the very top, and then there is another option for the formation of empty space (see right).The same elevation map is used at each step to identify empty areas.
In general, everything has been said. First we try to pack in empty areas, then in the lowest place, and last of all - from above, a degenerate case of the “lowest place”.
OF algorithm
Online fit
Input: The dimensions of the rectangles {w (Li); h (Li)} and the strip width W.
Output: The height H and the packing.
1: i = 0; H = 0
2: Create a linear array number of elements are equal to W
3: while there is an unpacked rectangle do
4: i ++
5: Li
6: if w (EmptyArea) ≥ w (Li) and h (EmptyArea) ≥ h (Li) then
7: pack rectangle in empty area
8: else
9: If the area is empty
10: Search for linear array for packing width
11: else [there is a space in linear array]
12: pack rectangle on top left justified
from the index leading to smaller space
13: end if
14: end if
15: end while
16: H = highest entry in the linear array
17: print H and entire packing Afterword
To dispel the sense of purposelessness of what is happening, I will give one of the classic, but inspiring examples of the application of algorithms for two-dimensional packaging in a semi-unlimited band. This is a task scheduler for a multiprocessor system. In modern software for clusters, more “adult” algorithms are used, but the planning task itself is reduced to 2DSP. Under the conditions of clusters, the flow of incoming tasks is nothing more than online data for packaging: the horizontal dimension is the required number of cores, the vertical is the task time. (Everything is like at the dawn of technology: you get in line to the computer and you warn in advance how much resources you need and how long your card will turn). The scheduler must allocate specific processors for the task and determine the launch moment. In its pure form, by the way, no algorithm can be used, as time drips while the scheduler is waiting for a task or is thinking about its placement. Additionally, the programmer can be tied by hands with different specific conditions: the priority of tasks; the ability to scale the task at runtime; hardware delays and system self-service, including redistribution taking into account failed resources; comparison of the nature of communications within the task with the cluster architecture, etc.
Any algorithm is beautiful in its mathematical rigor, until you start to apply it to real life.
And finally, the comparative characteristics of the algorithms in a pleasant, impersonal form. Here is the ratio of the optimal packing height (the sum of the areas of the rectangles divided by the width of the strip) to the resulting.
| NFL | Ffl | Bfl | BiNFL | Nfs | Ffs | Bfs | HS | Azar y | CPF | CFF | CC | Of |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.56 | 0.63 | 0.75 | 0.56 | 0.45 | 0.57 | 0.57 | 0.37 | 0.44 | 0.60 | 0.59 | 0.63 | 0.72 |
Code (Qt):
Algorithms packager.h packager.cpp
Gui window.h window.cpp renderarea.h renderarea.cpp main.cpp
Source: https://habr.com/ru/post/160869/
All Articles