Non-binary logic
At the beginning of World War II, the US Army faced an acute problem of a shortage of ballistic firing tables, vital for the work of artillery. A typical ballistic table is a set of numerical data of projectile flight paths, previously calculated for specific firing conditions, barrel, projectile, weather conditions and air temperature. Manual calculation of only one trajectory took several days, and each table managed in huge amounts of man-hours.
At that time, only a few highly qualified specialists were engaged in these calculations, and even an increase in the laboratory staff in 1942 did not help much. In June of the same year, a contract was concluded with the Moore School of Electrical Engineering of the University of Pennsylvania, which had a differential analyzer for the design of Vanivar Bush, the mechanical calculator of that era. The work was led by a lieutenant, and later Captain Hermann Goldstein, who received a doctorate in mathematics from the University of Chicago. It was he who with Professor Brainer in 1943 introduced the idea of an "electronic differential analyzer" by John Mockley.
The new machine, the project of which was rejected a year earlier for excessive novelty, began to perform real work only in the autumn of 1945. The wetlands, who previously worked with weather and physical data, predicted the future urgent need for a high-speed calculator, and although by the end of the construction there was no need to manufacture ballistic tables, the computer was in demand and was used in the design of nuclear and thermonuclear bomb, weather calculations and radioactive fallout , solving the problem of supersonic aircraft construction and calculating mathematical constants.
')
With its general primitiveness (for setting the program it was necessary to manually move the nodes and switches) and technical difficulties of operation associated with the unreliability of vacuum tubes, ENIAC impressed with its capabilities and speed, which was not limited by the presence of moving parts. Unlike other electromechanical machines of that era, which worked on electric relays, and its successor EDVAK, the first general-purpose electronic digital computer was not a binary, but a decimal one.

Decimal drives of computer ENIAC
The choice of the decimal system was dictated by questions of its ease of use; the creators of the machine decided to neglect the merits of other number systems. ENIAK could add, subtract, multiply, divide, extract the square root and compare any decimal numbers of 10 digits. In memory of 20 drives, which were also adders, up to 20 such numbers could be stored. The numbers were not represented by ten different electrical values, which could easily have changed, but by the absence or presence of active pulses, and a set of signals of the same number was transmitted together via several different wires. Thus, 11 lines approached each register (10 digits and a sign).
Each trigger of the machine had two inputs and two outputs and contained two triodes connected in such a way that at any moment the current passed through only one. Ten triggers formed a decimal ring capable of counting numeric signals and storing numbers. In turn, ten rings were combined into a basic arithmetic drive. If one of the rings went beyond the limit of 9 values, the older neighbor received an additional impulse.
The computer, which was essentially a mechanically programmable calculator, relied in its work on these drives. When added, one of the drives passed the digits of the corresponding digits to another, and when subtracted, it took them. Multiplication required four accumulators storing a multiplier, a multiplicand, and two cells for performing a mathematical operation. When dividing, the dividend, divisor, quotient and remainder shifted by digits for subtraction from the dividend were stored.
It is obvious that ENIAC was largely hardware redundant. Its complexity, caused by the use of such a “humane” decimal form of representing numbers on the basis of binary triggers, and the instability in the operation of vacuum tubes somewhat hampered its work and forced the staff to go for various tricks in its operation.
The latest machine upgrade took place in July 1953 (before ENIAC had acquired, for example, a mechanical power supply decoupling system). Already in 1951, the question of insufficient amount of memory arose, and Burroughs Corporation offered to use promising technology of magnetic cells. The main problem of the performer was the language. To implement a 100-word memory in ENIAC, each of which was 10 decimal digits and 10 digits of these numbers, 9.100 bits of storage would be required. Instead, each digit was presented in the form of 4 bits with the introduction of code converters, but even taking into account the lost bits of the forbidden states, the savings were significant - only 4,100 bits were required.
A series of IBM, UNIVAC and other machines followed ENIAK, but decimal computers were gradually replaced by binary ones. The reasons for this are simple: the elementary logical elements common today have only two states that they can assume, so writing data in binary form is certainly simpler and denser. Sixty years later, a departure from binary logic is perceived as a losing step, but is binary mathematically the best choice?
The specific natural log density of the information is described by the function
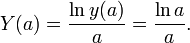
This function reaches a maximum at a = e. This means that the calculus system has the highest information recording density with a base equal to the base of natural logarithms (e ≈ 2.718281828459045). This is the way the basis was chosen for fixing logarithmic tables. At the same time, of the integer number systems, the ternary rather than binary number system has the highest information recording density.
The ternary number system exists in two versions: symmetric, having negative digits (−1, 0, 1) in the set, and asymmetric (0, 1, 2). It should be noted that the ternary symmetric number system has the property that provides a simpler representation of negative numbers in the computer's memory. (As it is known, for this purpose it is necessary to enter additional code in order to not complicate the computer architecture.)
The ternary computer operates with ternary logic, the first and most well-known multi-valued logic. Unlike binary logic, where a statement is assigned values either “true” or “false”, the ternary fuzzy logic has the state “unknown”. The advantage of three-digit logic over a binary is best demonstrated by comparing two numbers: here the ternary logic immediately gives the result (more, less or equal), and the binary answer requires you to first find out if the first is greater than the second and then make sure the second first.
Not all laws of binary logic are true for the ternary logic, for some ternary analogs are formulated. A number of researchers appeals to the fact that three-valued logic is much more natural and peculiar to human thinking than binary. Today, obsolete binary logic, according to their statements, does not allow us to enter the three-digit one. The development of the ternary logic in different periods of time involved the Polish philosopher and logician Jan Lukasevich, the English mathematician Lewis Carroll and others.
Despite all the advantages of the ternary logic and the ternary number system, in the history of mankind there are only two of the most successful attempts to create a ternary computer. The first of these, mechanical, dates back to the 19th century. Fowler's wooden calculator used a symmetrical threefold number system, and Augustus de Morgan made the most accurate description of it today, on the basis of which the machine was recreated.

Fearing the theft of his ideas, Fowler single-handedly made wood parts. To compensate for the low accuracy caused by it, the inventor gave his car large dimensions - 1.80 meters in length, 90 cm in depth and 30 cm in height. Before that, Fowler had developed methods for working with the number system used in his car.
The machine consists of four parts. Depending on the operation being performed, the first part (highlighted in red in the figure) is multiplicable or partial, the second (highlighted in blue) is a multiplier or divisor, the third (highlighted in burgundy) is a work or dividend, the fourth is a transfer apparatus that simplifies the answer to its simplest forms after performing basic operations and can be moved for this to a multiplier or divisor to work with them.
The multiplier is a frame that can move perpendicular to the rods of the multiplicable and the product, and is located between their planes in such a way that its edge can be combined with a sliding movement with each pivot of the multiplicand in turn. The multiplier consists of a set of rods, with each of the rods having a prong at each edge and a prong that interacts with the multiplier with the multiplier rods. One set of teeth is placed so that it rests on the frame, which can rotate around an axis. Each rod may come into contact with the frame above, below or around the axis of rotation. The teeth on the axis do not receive movement, the rest will move in one direction or another, depending on which side the tooth touches the frame. Perpendicular teeth from the other end can move back and forth or remain motionless, in turn, they thereby interact with the rods, which make up the frame of the work, which is similar to the frame of the multiplicand and has a detail connecting it with the multiplier.

When multiplying, the frame of the multiplier is set so that the edge of the multiplier coincides with the first rod of the multiplicand. From the edge there is a fixed tooth, which engages with the rod of the multiplicand above which it appears, moving it in one direction or another according to which direction the frame of the multiplier can turn. Then the rotating frame must be moved in such a way that the rod of the multiplicand falls to zero. This multiplies the multiplier of the multiplicand with the multiplier. Then the action of perpendicular teeth displays the result on the frame of the work. The frame of the multiplier is shifted until the tooth is above the next rod of the multiplicand, then the tooth is shifted so that the next rod of the multiplicand is moved to the zero position. The next digit of the multiplicand will be multiplied by the multiplier, and the frame of the product will receive and add it. The operation is repeated until the multiplicative digits run out.
The result of the multiplication will not be represented in the simplest form: it must contain only +1 or −1, and the resulting intermediate answer can contain +2, −2, +3 or −3, etc. on any bar. To adjust the result, a transfer mechanism is used, which is a simple device that, like a multiplier, can make lateral movement, and can be placed on any pair of adjacent rods. The transfer apparatus advances the left of the two rods by one and retracts the rod to the right by 3 units or vice versa. Even without the presence of the obligatory skill of working with the transfer mechanism, a serious mistake is impossible, since for each operation the lower column can be transferred only by 3 units, while the next column will change in the opposite direction by one unit.
The division of numbers is the opposite way.
The second most successful project of the ternary computing machine is the relatively modern serial (50 copies) Setun computer built at the MSU computer center in 1959. Its creator is the Soviet designer Nikolai Petrovich Brusentsov, and E.A. Zhogolev, V.V. Verigin, S.P. Maslov, A.M. Tishulina et al. The machine used a symmetrical trinity system.

Setun's minimum addressable unit of memory is a six-trit night and takes values from -364 to 364. Working with a range of negative values is a feature that distinguishes a treyt from a binary byte, the values of which extend from 0 to 255. With the help of a treyt, you can encode everything upper and lower case symbols of the Russian and Latin alphabets, necessary mathematical and service symbols.
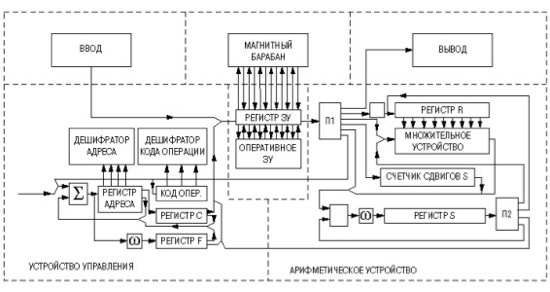
The machine was not realized on unreliable vacuum tubes or transistors that were expensive at that time, but on ferrite-diode elements assembled on the basis of a gain. The clock generator set the clock operation of the cells at 200 kHz. The cells were assembled into functional blocks: adders, decoder ternary code, shift registers. With the help of a thirty-contact connector, each unit was connected to other “Setun” blocks, forming the basic components of a computer: an arithmetic unit and a control unit
When designing, Brusentsov borrowed the principle of operation of logic elements from the LEM-1 computer, but while the latter uses a pair of cores for each bit - work and compensation, the compensation core works in Setun, which sets the ternary character of the computer. In the ternary Brusentsov cell, one trit was recorded in two binary digits, the fourth state of two binary digits was not used.
The first prototype of the Setun machine showed 95% of useful time during tests (real work outside testing, maintenance and troubleshooting), while 60% was considered a good result. At the expense of simple technologies "Setun" with all the periphery cost 27.5 thousand rubles (for comparison: only the processor unit was record-breaking cheap PDP-8 cost 20 thousand dollars), and the car showed interest not only in the socialist countries, but also in the West. The Czechoslovak Zbroevka Yana Šverma factory was ready to start producing cars for buyers abroad and promised a benefit of half a million dollars from each car, but higher management required first to start mass production of cars in the USSR, although it was already then that the project was nearing closure.
And the project was really closed. In 1967, when it was decided to make various production gifts for the 100th anniversary of the birth of Lenin, the designers, some of whom had already changed jobs, undertook to make Setun-70, an improved version of the original, for this date. It was a slightly different computer: it was a stack, but unlike Elbrus with its operand stack and later PDP-11 with its procedural stack, Setun-70 had two stacks - commands and operands. As Brusentsov himself says, the programs on the “Setun-70” turned out to be easily readable and easily mastered, and instead of debugging a control assembly was used — a pass of the written code from bottom to top. Later, “Setun-70” was emulated on binary machines in the form of an interactive system for structured programming of PRSP , but the developers, having the bitter experience of “Setun”, naturally did not make any attempts to replicate “Setun-70”.

We should not think that today the ternary logic has been completely forgotten: it is used in telecommunications, where the speed of information transfer is important. Sending one trit per cycle increases the data transfer rate for one digit by 1.5 times per bit, with an increase in the number of digits, the rate increases exponentially, while the unit hardware costs decrease.
IBM, Motorola, Hypres and Texas Instruments conduct various studies in the field of ternary computers. Significant hardware problems in the implementation of three-valued logic today does not exist; on the contrary, new and new promising elements with three states are proposed. In the framework of silicon-germanium alloys (SiGe), you can implement digital integrated circuits that work with three or more signal levels.
In their scientific work “The Architecture of the Ternary Optical Computer ” Jin Yi, Hee Huacan and Lu Yangtian offer to use two states of polarization of light with orthogonal directions of oscillation to express information. Three researchers propose to use a fiber ring as a register, a semiconductor memory for a ternary cell, and liquid crystals as modulators and adders.
It should be remembered about the whole complex of shortcomings of the ternary logic. For example, logical elements with three states will cost more, and designing a computer based on them will be fraught with various difficulties.
For the productive work of a ternary computer, you need a lot of quality ternary software, which does not exist now. To date, several thousand man-years and billions of dollars have been spent on some binary software projects, and recreating from scratch such a three-valued logic would be too expensive.
Otherwise, the ternary computer is mathematically the best solution, and the peculiarities of the work of its logic, as well as the representation of negative numbers, indicate this. It remains to hope that our attitude towards the ternary logic will change with time.
« », mortarti.com , trinary.ru , trinitas.ru , .
At that time, only a few highly qualified specialists were engaged in these calculations, and even an increase in the laboratory staff in 1942 did not help much. In June of the same year, a contract was concluded with the Moore School of Electrical Engineering of the University of Pennsylvania, which had a differential analyzer for the design of Vanivar Bush, the mechanical calculator of that era. The work was led by a lieutenant, and later Captain Hermann Goldstein, who received a doctorate in mathematics from the University of Chicago. It was he who with Professor Brainer in 1943 introduced the idea of an "electronic differential analyzer" by John Mockley.
The new machine, the project of which was rejected a year earlier for excessive novelty, began to perform real work only in the autumn of 1945. The wetlands, who previously worked with weather and physical data, predicted the future urgent need for a high-speed calculator, and although by the end of the construction there was no need to manufacture ballistic tables, the computer was in demand and was used in the design of nuclear and thermonuclear bomb, weather calculations and radioactive fallout , solving the problem of supersonic aircraft construction and calculating mathematical constants.
')
With its general primitiveness (for setting the program it was necessary to manually move the nodes and switches) and technical difficulties of operation associated with the unreliability of vacuum tubes, ENIAC impressed with its capabilities and speed, which was not limited by the presence of moving parts. Unlike other electromechanical machines of that era, which worked on electric relays, and its successor EDVAK, the first general-purpose electronic digital computer was not a binary, but a decimal one.

Decimal drives of computer ENIAC
The choice of the decimal system was dictated by questions of its ease of use; the creators of the machine decided to neglect the merits of other number systems. ENIAK could add, subtract, multiply, divide, extract the square root and compare any decimal numbers of 10 digits. In memory of 20 drives, which were also adders, up to 20 such numbers could be stored. The numbers were not represented by ten different electrical values, which could easily have changed, but by the absence or presence of active pulses, and a set of signals of the same number was transmitted together via several different wires. Thus, 11 lines approached each register (10 digits and a sign).
Each trigger of the machine had two inputs and two outputs and contained two triodes connected in such a way that at any moment the current passed through only one. Ten triggers formed a decimal ring capable of counting numeric signals and storing numbers. In turn, ten rings were combined into a basic arithmetic drive. If one of the rings went beyond the limit of 9 values, the older neighbor received an additional impulse.
The computer, which was essentially a mechanically programmable calculator, relied in its work on these drives. When added, one of the drives passed the digits of the corresponding digits to another, and when subtracted, it took them. Multiplication required four accumulators storing a multiplier, a multiplicand, and two cells for performing a mathematical operation. When dividing, the dividend, divisor, quotient and remainder shifted by digits for subtraction from the dividend were stored.
It is obvious that ENIAC was largely hardware redundant. Its complexity, caused by the use of such a “humane” decimal form of representing numbers on the basis of binary triggers, and the instability in the operation of vacuum tubes somewhat hampered its work and forced the staff to go for various tricks in its operation.
The latest machine upgrade took place in July 1953 (before ENIAC had acquired, for example, a mechanical power supply decoupling system). Already in 1951, the question of insufficient amount of memory arose, and Burroughs Corporation offered to use promising technology of magnetic cells. The main problem of the performer was the language. To implement a 100-word memory in ENIAC, each of which was 10 decimal digits and 10 digits of these numbers, 9.100 bits of storage would be required. Instead, each digit was presented in the form of 4 bits with the introduction of code converters, but even taking into account the lost bits of the forbidden states, the savings were significant - only 4,100 bits were required.
A series of IBM, UNIVAC and other machines followed ENIAK, but decimal computers were gradually replaced by binary ones. The reasons for this are simple: the elementary logical elements common today have only two states that they can assume, so writing data in binary form is certainly simpler and denser. Sixty years later, a departure from binary logic is perceived as a losing step, but is binary mathematically the best choice?
The specific natural log density of the information is described by the function
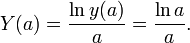
This function reaches a maximum at a = e. This means that the calculus system has the highest information recording density with a base equal to the base of natural logarithms (e ≈ 2.718281828459045). This is the way the basis was chosen for fixing logarithmic tables. At the same time, of the integer number systems, the ternary rather than binary number system has the highest information recording density.
The ternary number system exists in two versions: symmetric, having negative digits (−1, 0, 1) in the set, and asymmetric (0, 1, 2). It should be noted that the ternary symmetric number system has the property that provides a simpler representation of negative numbers in the computer's memory. (As it is known, for this purpose it is necessary to enter additional code in order to not complicate the computer architecture.)
The ternary computer operates with ternary logic, the first and most well-known multi-valued logic. Unlike binary logic, where a statement is assigned values either “true” or “false”, the ternary fuzzy logic has the state “unknown”. The advantage of three-digit logic over a binary is best demonstrated by comparing two numbers: here the ternary logic immediately gives the result (more, less or equal), and the binary answer requires you to first find out if the first is greater than the second and then make sure the second first.
Not all laws of binary logic are true for the ternary logic, for some ternary analogs are formulated. A number of researchers appeals to the fact that three-valued logic is much more natural and peculiar to human thinking than binary. Today, obsolete binary logic, according to their statements, does not allow us to enter the three-digit one. The development of the ternary logic in different periods of time involved the Polish philosopher and logician Jan Lukasevich, the English mathematician Lewis Carroll and others.
Despite all the advantages of the ternary logic and the ternary number system, in the history of mankind there are only two of the most successful attempts to create a ternary computer. The first of these, mechanical, dates back to the 19th century. Fowler's wooden calculator used a symmetrical threefold number system, and Augustus de Morgan made the most accurate description of it today, on the basis of which the machine was recreated.

Fearing the theft of his ideas, Fowler single-handedly made wood parts. To compensate for the low accuracy caused by it, the inventor gave his car large dimensions - 1.80 meters in length, 90 cm in depth and 30 cm in height. Before that, Fowler had developed methods for working with the number system used in his car.
The machine consists of four parts. Depending on the operation being performed, the first part (highlighted in red in the figure) is multiplicable or partial, the second (highlighted in blue) is a multiplier or divisor, the third (highlighted in burgundy) is a work or dividend, the fourth is a transfer apparatus that simplifies the answer to its simplest forms after performing basic operations and can be moved for this to a multiplier or divisor to work with them.
The multiplier is a frame that can move perpendicular to the rods of the multiplicable and the product, and is located between their planes in such a way that its edge can be combined with a sliding movement with each pivot of the multiplicand in turn. The multiplier consists of a set of rods, with each of the rods having a prong at each edge and a prong that interacts with the multiplier with the multiplier rods. One set of teeth is placed so that it rests on the frame, which can rotate around an axis. Each rod may come into contact with the frame above, below or around the axis of rotation. The teeth on the axis do not receive movement, the rest will move in one direction or another, depending on which side the tooth touches the frame. Perpendicular teeth from the other end can move back and forth or remain motionless, in turn, they thereby interact with the rods, which make up the frame of the work, which is similar to the frame of the multiplicand and has a detail connecting it with the multiplier.

When multiplying, the frame of the multiplier is set so that the edge of the multiplier coincides with the first rod of the multiplicand. From the edge there is a fixed tooth, which engages with the rod of the multiplicand above which it appears, moving it in one direction or another according to which direction the frame of the multiplier can turn. Then the rotating frame must be moved in such a way that the rod of the multiplicand falls to zero. This multiplies the multiplier of the multiplicand with the multiplier. Then the action of perpendicular teeth displays the result on the frame of the work. The frame of the multiplier is shifted until the tooth is above the next rod of the multiplicand, then the tooth is shifted so that the next rod of the multiplicand is moved to the zero position. The next digit of the multiplicand will be multiplied by the multiplier, and the frame of the product will receive and add it. The operation is repeated until the multiplicative digits run out.
The result of the multiplication will not be represented in the simplest form: it must contain only +1 or −1, and the resulting intermediate answer can contain +2, −2, +3 or −3, etc. on any bar. To adjust the result, a transfer mechanism is used, which is a simple device that, like a multiplier, can make lateral movement, and can be placed on any pair of adjacent rods. The transfer apparatus advances the left of the two rods by one and retracts the rod to the right by 3 units or vice versa. Even without the presence of the obligatory skill of working with the transfer mechanism, a serious mistake is impossible, since for each operation the lower column can be transferred only by 3 units, while the next column will change in the opposite direction by one unit.
The division of numbers is the opposite way.
The second most successful project of the ternary computing machine is the relatively modern serial (50 copies) Setun computer built at the MSU computer center in 1959. Its creator is the Soviet designer Nikolai Petrovich Brusentsov, and E.A. Zhogolev, V.V. Verigin, S.P. Maslov, A.M. Tishulina et al. The machine used a symmetrical trinity system.

Setun's minimum addressable unit of memory is a six-trit night and takes values from -364 to 364. Working with a range of negative values is a feature that distinguishes a treyt from a binary byte, the values of which extend from 0 to 255. With the help of a treyt, you can encode everything upper and lower case symbols of the Russian and Latin alphabets, necessary mathematical and service symbols.

The machine was not realized on unreliable vacuum tubes or transistors that were expensive at that time, but on ferrite-diode elements assembled on the basis of a gain. The clock generator set the clock operation of the cells at 200 kHz. The cells were assembled into functional blocks: adders, decoder ternary code, shift registers. With the help of a thirty-contact connector, each unit was connected to other “Setun” blocks, forming the basic components of a computer: an arithmetic unit and a control unit
When designing, Brusentsov borrowed the principle of operation of logic elements from the LEM-1 computer, but while the latter uses a pair of cores for each bit - work and compensation, the compensation core works in Setun, which sets the ternary character of the computer. In the ternary Brusentsov cell, one trit was recorded in two binary digits, the fourth state of two binary digits was not used.
The first prototype of the Setun machine showed 95% of useful time during tests (real work outside testing, maintenance and troubleshooting), while 60% was considered a good result. At the expense of simple technologies "Setun" with all the periphery cost 27.5 thousand rubles (for comparison: only the processor unit was record-breaking cheap PDP-8 cost 20 thousand dollars), and the car showed interest not only in the socialist countries, but also in the West. The Czechoslovak Zbroevka Yana Šverma factory was ready to start producing cars for buyers abroad and promised a benefit of half a million dollars from each car, but higher management required first to start mass production of cars in the USSR, although it was already then that the project was nearing closure.
And the project was really closed. In 1967, when it was decided to make various production gifts for the 100th anniversary of the birth of Lenin, the designers, some of whom had already changed jobs, undertook to make Setun-70, an improved version of the original, for this date. It was a slightly different computer: it was a stack, but unlike Elbrus with its operand stack and later PDP-11 with its procedural stack, Setun-70 had two stacks - commands and operands. As Brusentsov himself says, the programs on the “Setun-70” turned out to be easily readable and easily mastered, and instead of debugging a control assembly was used — a pass of the written code from bottom to top. Later, “Setun-70” was emulated on binary machines in the form of an interactive system for structured programming of PRSP , but the developers, having the bitter experience of “Setun”, naturally did not make any attempts to replicate “Setun-70”.

We should not think that today the ternary logic has been completely forgotten: it is used in telecommunications, where the speed of information transfer is important. Sending one trit per cycle increases the data transfer rate for one digit by 1.5 times per bit, with an increase in the number of digits, the rate increases exponentially, while the unit hardware costs decrease.
IBM, Motorola, Hypres and Texas Instruments conduct various studies in the field of ternary computers. Significant hardware problems in the implementation of three-valued logic today does not exist; on the contrary, new and new promising elements with three states are proposed. In the framework of silicon-germanium alloys (SiGe), you can implement digital integrated circuits that work with three or more signal levels.
In their scientific work “The Architecture of the Ternary Optical Computer ” Jin Yi, Hee Huacan and Lu Yangtian offer to use two states of polarization of light with orthogonal directions of oscillation to express information. Three researchers propose to use a fiber ring as a register, a semiconductor memory for a ternary cell, and liquid crystals as modulators and adders.
It should be remembered about the whole complex of shortcomings of the ternary logic. For example, logical elements with three states will cost more, and designing a computer based on them will be fraught with various difficulties.
For the productive work of a ternary computer, you need a lot of quality ternary software, which does not exist now. To date, several thousand man-years and billions of dollars have been spent on some binary software projects, and recreating from scratch such a three-valued logic would be too expensive.
Otherwise, the ternary computer is mathematically the best solution, and the peculiarities of the work of its logic, as well as the representation of negative numbers, indicate this. It remains to hope that our attitude towards the ternary logic will change with time.
« », mortarti.com , trinary.ru , trinitas.ru , .
Source: https://habr.com/ru/post/160595/
All Articles