Collection Overhead
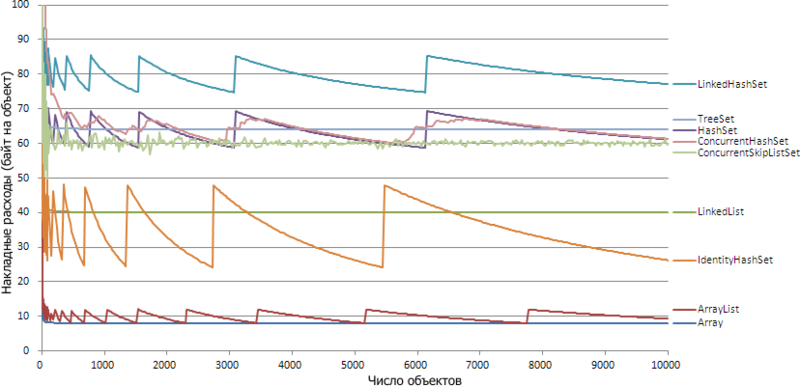
I was wondering which collections eat as much as extra memory when storing objects. I took measurements of overheads for popular collections that involve storing items of the same type (that is, lists and sets) and put the results on a general schedule. Here is a picture for the 64-bit Hotspot JVM (Java 1.6):
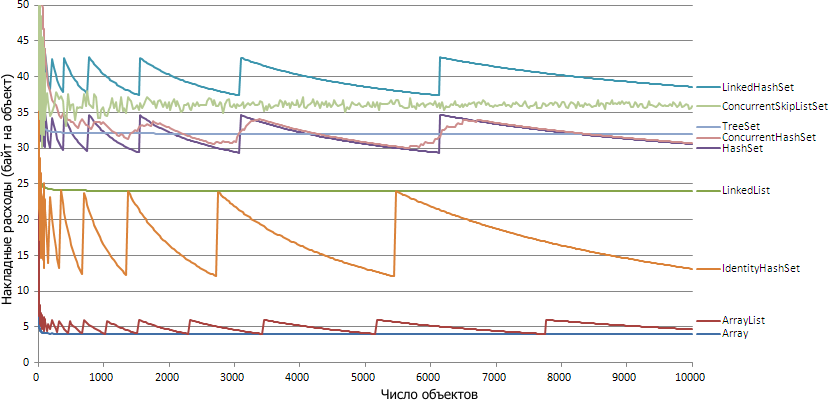
But for 32-bit Hotspot:
Below I will tell you how the measurements were taken, and then try to figure out why the pictures look that way.
Measurements were performed for standard Java collections from java.util and java.util.concurrent, as well as for a regular Java array. The IdentityHashSet and ConcurrentHashSet collections are created from the corresponding Map using the Collections.newSetFromMap () method. All collections were initialized by default without first specifying the number of elements (well, except for the array, for which this is mandatory), and then filled with test objects using the add method (and assignment was simply performed for the array). About 500 collections of each type were created with a different number of elements from 1 to 10,000. As elements, 10,000 different rows of random length were used, consisting of random letters. In principle, the elements themselves affect only the ConcurrentHashSet, and even that is insignificant, so the graphs will look similar for any data.
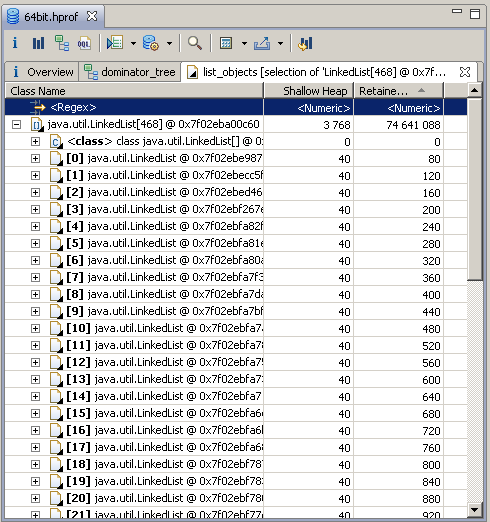
After filling in the arrays, a memory dump was taken from the process and analyzed using the Eclipse Memory Analyzer, which very correctly calculated the Retained set of each of the collections, not including the objects themselves, but only including the overhead. It looks like this, for example:
Well, then copy in Excel, simple mathematical operations and plotting with a little drawing in a graphical editor.
')
It can be seen that each collection has a lower overhead limit and the more elements there are, the more often it becomes close to it. However, for some collections it cannot be said that the overhead function converges to this boundary in a mathematical sense. For example, ArrayList although it is increasingly at the value of 8 bytes (for 64bit), but it continues to jump to the value of 12 bytes with each new memory allocation.
Interestingly, the graphs for 32bit and 64bit are very similar: for most collections, the graphics differ by half except for two exceptions: ConcurrentSkipListSet and LinkedList. Consider each collection separately and see why it’s such a schedule.
The simplest option is an array, for which the number of elements is known in advance. It contains the reference for each object: 4 (8) bytes (the value for 64-bit JVM is in parentheses), in addition, the array length is stored - int, 4 bytes, and the object descriptor is 8 (16) bytes. In addition, each object is aligned by 8 bytes, due to which arrays with an even number of elements per 32bit lose 4 bytes. Result: 4 (8) bytes per object plus a constant from 12 to 24 bytes.
An empty array is 16 (24) bytes.
There is almost the same with a slight difference: since the number of elements in the array is unknown in advance, the array is allocated with a margin (by default 10 elements) and, if necessary, expands a little more than one and a half times:
Therefore, the schedule jumps to 6 (12) bytes. The constant is also slightly larger: 40 (64) bytes, since in addition to the array, there is the ArrayList object itself, which stores the link to the array, the actual size of the list, and the number of modifications (for throwing ConcurrentModificationException). However, this is the most economical way to store data of the same type, if you do not know in advance how many of them will be.
The default ArrayList without elements takes 80 (144) bytes.
For a linked list, the picture looks like an array: tends to asymptote along a hyperbola. For each element of the list, one service object of the java.util.LinkedList.Entry type is created. Each of these objects contains three links (to the list item itself, to the previous and next Entry), while due to alignment, 32 bytes are lost by 4 bytes, so 24 (40) bytes are required for each Entry. The constant includes the handle of the LinkedList object, the head Entry and a link to it, the size of the list and the number of modifications, and is 48 (80) bytes. The same takes an empty list, since no memory is reserved here, of course, is not allocated.
In general, all sets used are based on Map. A separate implementation in some cases could be somewhat more compact, but the general code is, of course, more important.
The graph is also similar to LinkedList and an array. For each element, a java.util.TreeMap.Entry tree branch is created, which contains five links: a key, a value, a parent, a left and right child. In addition to these, a boolean variable is stored, indicating the color of the branch, red or black (see red-black tree ). A separate Boolean variable is 4 bytes, so the entire record is 32 (64) bytes.
The persistent data in the TreeMap is as follows: a reference to the comparator, a link to the root of the tree (as opposed to a headstone Entry in LinkedList, the root is used for its intended purpose — it refers to the real element of the set) size and number of modifications. With a handle to the TreeMap object, 48 (80) bytes are obtained. The TreeSet itself adds only its descriptor and a link to the TreeMap. The total is 64 (104) bytes. An empty set weighs the same. By the way, the memory consumption does not depend on the degree of balance of the tree.
HashSet is based on HashMap, which is somewhat trickier than TreeMap. For each element, a java.util.HashMap.Entry entry is created containing references to the key, the value following Entry (if several entries fall into one hash table cell), and the hash value itself. Total Entry weighs 24 (48) bytes.
In addition to Entry, there is also a hash table, with links to Entry, which contains 16 elements initially and doubles when the number of elements exceeds 75% of its size (75% is the default loadFactor value, it can be specified in the constructor). That is, when designing by default, an increase in the table occurs when the number of elements exceeds 12, 24, 48, 96, etc. (2 n * 3, the last burst on the graph is 6144 elements). Immediately after the increase, the table is 2 / 0.75 = 2.67 times the number of elements, that is, the total consumption is about 34.67 (69.33) bytes per element (not counting the constant). Immediately before the increase, the table is only 1 / 0.75 = 1.33 times the number of elements, and the total consumption is 29.33 (58.67) bytes per element. Note that the memory consumption is completely independent of how often hash collisions occur.
Those who wish can calculate the constant component themselves, I will only say that the initialized, empty HashSet by default weighs 136 (240) bytes.
Almost the same as in HashSet. It uses java.util.LinkedHashMap.Entry, which inherits java.util.HashMap.Entry, adding two links to the previous and next elements, so the graph is 8 (16) bytes higher than for HashSet, reaching before extending the table 37.33 (74.67) , and after - a record 42.67 (85.33). The constant has also increased, since, like LinkedList, the head Entry is stored, which does not refer to the element of the set. Freshly created LinkedHashSet weighs 176 (320) bytes.
IdentityHashMap is a very interesting thing. It violates the standard Map contract by comparing == keys, not equals, and using System.identityHashCode. It is also interesting because it does not create objects like Entry, but simply stores all keys and values in one array (keys in even elements, values in odd ones). In the event of a collision, it does not create a list, but writes the object to the first free cell along the course of the array. Thanks to it record-breaking low overhead costs among all sets are reached.
IdentityHashMap doubles the size of the array every time it is more than 2/3 full (unlike HashMap, this ratio is not adjustable). By default, an array is created on 32 elements (that is, the size of the array is 64). Accordingly, the expansion occurs when exceeding 21, 42, 85, 170, etc. ([2 n / 3], the last burst on the chart is 5461). Before the expansion, the array contains 3 times more elements than the keys in the IdentityHashMap, and after the expansion - 6 times. Thus, overhead costs range from 12 (24) to 24 (48) bytes per element. The empty set by default takes quite a lot - 344 (656) bytes, but already with nine elements it becomes more economical than all other sets.
ConcurrentHashMap is the first collection in which the graph depends on the elements themselves (or rather on their hash functions). Roughly speaking, this is a set of a fixed number of segments (there are 16 by default), each of which is a synchronous analogue of a HashMap. Part of the bits from the modified hash code is used to select a segment, access to different segments can occur in parallel. In the limit, the overheads coincide with the overheads of the HashMap itself, because java.util.concurrent.ConcurrentHashMap.HashEntry is arranged almost the same as java.util.HashMap.Entry. The increase in the size of the segments occurs independently, because the graph does not rise simultaneously: first, the segments in which more elements fall are enlarged.
This collection came out on top in the initial size - 1304 (2328) bytes, because it immediately gets 16 segments, each of which has a table with 16 records and several auxiliary fields. However, for 10,000 ConcurrentHashSet elements, HashSet is just 0.3% larger.
Implemented through ConcurrentSkipListMap and, in my opinion, the most difficult of the collections described. The idea of the algorithm was described on Habré , so here I will not go into the details. I note only that the resulting amount of memory here is independent of the data, but it is nondetermined, since the collection is initiated by a pseudo-random number generator. Based on the next pseudo-random number, the decision is made whether to add an index entry and how many levels. For each element, one java.util.concurrent.ConcurrentSkipListMap.Node object is created, which contains references to the key, the value and the next Node, forming a simply linked list. This gives 24 (40) bytes for each item. In addition, approximately one index entry is created (java.util.concurrent.ConcurrentSkipListMap.Index) for every two entries (on the first level there is an index for every fourth entry, on the second for every eighth entry, etc.). Each index entry weighs as much as Node (there are also three links), so in total each item requires about 36 (60) bytes. There are still head entries for each level (HeadIndex), but there are few of them (approximately the logarithm of the number of elements), so they can be neglected.
An empty ConcurrentSkipListSet creates one HeadIndex and one empty Node; after construction, the default collection is 112 (200) bytes.
The results were largely unexpected and contradicted my intuitive ideas. So I thought that concurrent collections should be noticeably larger than regular ones, and LinkedHashSet should be located somewhere between TreeSet and HashSet. It also turned out to be surprising that practically anywhere memory consumption does not depend on the objects themselves: the degree of tree balance or the number of collisions in hash tables does not affect anything and for noncompetitive collections, you can determine in advance the size of overhead costs with a precision of up to a byte. It was interesting to delve into the internal structure of different collections. Is there any concrete practical use in this study? I don’t know, let everyone decide for himself.

But for 32-bit Hotspot:

Below I will tell you how the measurements were taken, and then try to figure out why the pictures look that way.
Materials and methods
Measurements were performed for standard Java collections from java.util and java.util.concurrent, as well as for a regular Java array. The IdentityHashSet and ConcurrentHashSet collections are created from the corresponding Map using the Collections.newSetFromMap () method. All collections were initialized by default without first specifying the number of elements (well, except for the array, for which this is mandatory), and then filled with test objects using the add method (and assignment was simply performed for the array). About 500 collections of each type were created with a different number of elements from 1 to 10,000. As elements, 10,000 different rows of random length were used, consisting of random letters. In principle, the elements themselves affect only the ConcurrentHashSet, and even that is insignificant, so the graphs will look similar for any data.
After filling in the arrays, a memory dump was taken from the process and analyzed using the Eclipse Memory Analyzer, which very correctly calculated the Retained set of each of the collections, not including the objects themselves, but only including the overhead. It looks like this, for example:

Well, then copy in Excel, simple mathematical operations and plotting with a little drawing in a graphical editor.
')
The discussion of the results
It can be seen that each collection has a lower overhead limit and the more elements there are, the more often it becomes close to it. However, for some collections it cannot be said that the overhead function converges to this boundary in a mathematical sense. For example, ArrayList although it is increasingly at the value of 8 bytes (for 64bit), but it continues to jump to the value of 12 bytes with each new memory allocation.
Interestingly, the graphs for 32bit and 64bit are very similar: for most collections, the graphics differ by half except for two exceptions: ConcurrentSkipListSet and LinkedList. Consider each collection separately and see why it’s such a schedule.
Array
The simplest option is an array, for which the number of elements is known in advance. It contains the reference for each object: 4 (8) bytes (the value for 64-bit JVM is in parentheses), in addition, the array length is stored - int, 4 bytes, and the object descriptor is 8 (16) bytes. In addition, each object is aligned by 8 bytes, due to which arrays with an even number of elements per 32bit lose 4 bytes. Result: 4 (8) bytes per object plus a constant from 12 to 24 bytes.
An empty array is 16 (24) bytes.
ArrayList
There is almost the same with a slight difference: since the number of elements in the array is unknown in advance, the array is allocated with a margin (by default 10 elements) and, if necessary, expands a little more than one and a half times:
int newCapacity = (oldCapacity * 3)/2 + 1; Therefore, the schedule jumps to 6 (12) bytes. The constant is also slightly larger: 40 (64) bytes, since in addition to the array, there is the ArrayList object itself, which stores the link to the array, the actual size of the list, and the number of modifications (for throwing ConcurrentModificationException). However, this is the most economical way to store data of the same type, if you do not know in advance how many of them will be.
The default ArrayList without elements takes 80 (144) bytes.
Linkedlist
For a linked list, the picture looks like an array: tends to asymptote along a hyperbola. For each element of the list, one service object of the java.util.LinkedList.Entry type is created. Each of these objects contains three links (to the list item itself, to the previous and next Entry), while due to alignment, 32 bytes are lost by 4 bytes, so 24 (40) bytes are required for each Entry. The constant includes the handle of the LinkedList object, the head Entry and a link to it, the size of the list and the number of modifications, and is 48 (80) bytes. The same takes an empty list, since no memory is reserved here, of course, is not allocated.
Treeset
In general, all sets used are based on Map. A separate implementation in some cases could be somewhat more compact, but the general code is, of course, more important.
The graph is also similar to LinkedList and an array. For each element, a java.util.TreeMap.Entry tree branch is created, which contains five links: a key, a value, a parent, a left and right child. In addition to these, a boolean variable is stored, indicating the color of the branch, red or black (see red-black tree ). A separate Boolean variable is 4 bytes, so the entire record is 32 (64) bytes.
The persistent data in the TreeMap is as follows: a reference to the comparator, a link to the root of the tree (as opposed to a headstone Entry in LinkedList, the root is used for its intended purpose — it refers to the real element of the set) size and number of modifications. With a handle to the TreeMap object, 48 (80) bytes are obtained. The TreeSet itself adds only its descriptor and a link to the TreeMap. The total is 64 (104) bytes. An empty set weighs the same. By the way, the memory consumption does not depend on the degree of balance of the tree.
Hashset
HashSet is based on HashMap, which is somewhat trickier than TreeMap. For each element, a java.util.HashMap.Entry entry is created containing references to the key, the value following Entry (if several entries fall into one hash table cell), and the hash value itself. Total Entry weighs 24 (48) bytes.
In addition to Entry, there is also a hash table, with links to Entry, which contains 16 elements initially and doubles when the number of elements exceeds 75% of its size (75% is the default loadFactor value, it can be specified in the constructor). That is, when designing by default, an increase in the table occurs when the number of elements exceeds 12, 24, 48, 96, etc. (2 n * 3, the last burst on the graph is 6144 elements). Immediately after the increase, the table is 2 / 0.75 = 2.67 times the number of elements, that is, the total consumption is about 34.67 (69.33) bytes per element (not counting the constant). Immediately before the increase, the table is only 1 / 0.75 = 1.33 times the number of elements, and the total consumption is 29.33 (58.67) bytes per element. Note that the memory consumption is completely independent of how often hash collisions occur.
Those who wish can calculate the constant component themselves, I will only say that the initialized, empty HashSet by default weighs 136 (240) bytes.
LinkedHashSet
Almost the same as in HashSet. It uses java.util.LinkedHashMap.Entry, which inherits java.util.HashMap.Entry, adding two links to the previous and next elements, so the graph is 8 (16) bytes higher than for HashSet, reaching before extending the table 37.33 (74.67) , and after - a record 42.67 (85.33). The constant has also increased, since, like LinkedList, the head Entry is stored, which does not refer to the element of the set. Freshly created LinkedHashSet weighs 176 (320) bytes.
IdentityHashSet (via newSetFromMap)
IdentityHashMap is a very interesting thing. It violates the standard Map contract by comparing == keys, not equals, and using System.identityHashCode. It is also interesting because it does not create objects like Entry, but simply stores all keys and values in one array (keys in even elements, values in odd ones). In the event of a collision, it does not create a list, but writes the object to the first free cell along the course of the array. Thanks to it record-breaking low overhead costs among all sets are reached.
IdentityHashMap doubles the size of the array every time it is more than 2/3 full (unlike HashMap, this ratio is not adjustable). By default, an array is created on 32 elements (that is, the size of the array is 64). Accordingly, the expansion occurs when exceeding 21, 42, 85, 170, etc. ([2 n / 3], the last burst on the chart is 5461). Before the expansion, the array contains 3 times more elements than the keys in the IdentityHashMap, and after the expansion - 6 times. Thus, overhead costs range from 12 (24) to 24 (48) bytes per element. The empty set by default takes quite a lot - 344 (656) bytes, but already with nine elements it becomes more economical than all other sets.
ConcurrentHashSet (via newSetFromMap)
ConcurrentHashMap is the first collection in which the graph depends on the elements themselves (or rather on their hash functions). Roughly speaking, this is a set of a fixed number of segments (there are 16 by default), each of which is a synchronous analogue of a HashMap. Part of the bits from the modified hash code is used to select a segment, access to different segments can occur in parallel. In the limit, the overheads coincide with the overheads of the HashMap itself, because java.util.concurrent.ConcurrentHashMap.HashEntry is arranged almost the same as java.util.HashMap.Entry. The increase in the size of the segments occurs independently, because the graph does not rise simultaneously: first, the segments in which more elements fall are enlarged.
This collection came out on top in the initial size - 1304 (2328) bytes, because it immediately gets 16 segments, each of which has a table with 16 records and several auxiliary fields. However, for 10,000 ConcurrentHashSet elements, HashSet is just 0.3% larger.
ConcurrentSkipListSet
Implemented through ConcurrentSkipListMap and, in my opinion, the most difficult of the collections described. The idea of the algorithm was described on Habré , so here I will not go into the details. I note only that the resulting amount of memory here is independent of the data, but it is nondetermined, since the collection is initiated by a pseudo-random number generator. Based on the next pseudo-random number, the decision is made whether to add an index entry and how many levels. For each element, one java.util.concurrent.ConcurrentSkipListMap.Node object is created, which contains references to the key, the value and the next Node, forming a simply linked list. This gives 24 (40) bytes for each item. In addition, approximately one index entry is created (java.util.concurrent.ConcurrentSkipListMap.Index) for every two entries (on the first level there is an index for every fourth entry, on the second for every eighth entry, etc.). Each index entry weighs as much as Node (there are also three links), so in total each item requires about 36 (60) bytes. There are still head entries for each level (HeadIndex), but there are few of them (approximately the logarithm of the number of elements), so they can be neglected.
An empty ConcurrentSkipListSet creates one HeadIndex and one empty Node; after construction, the default collection is 112 (200) bytes.
Why all this?
The results were largely unexpected and contradicted my intuitive ideas. So I thought that concurrent collections should be noticeably larger than regular ones, and LinkedHashSet should be located somewhere between TreeSet and HashSet. It also turned out to be surprising that practically anywhere memory consumption does not depend on the objects themselves: the degree of tree balance or the number of collisions in hash tables does not affect anything and for noncompetitive collections, you can determine in advance the size of overhead costs with a precision of up to a byte. It was interesting to delve into the internal structure of different collections. Is there any concrete practical use in this study? I don’t know, let everyone decide for himself.
Source: https://habr.com/ru/post/159557/
All Articles