Keccak, a new data hash standard
 Good day, dear readers.
Good day, dear readers.Many of you probably know that for several years NIST held a competition among the hash functions to adopt the new SHA-3 standard. And this year the award found its hero. The new standard has been safely accepted.
Well, since the standard has already been adopted, it's time to see what it is like.
And on a quiet Saturday night,
Prelude
The Keccak hash function with variable output lengths of 224,256,384 and 512 bits was chosen as the standard. At the heart of Keccak is a construction called Sponge (the sponge, the one from the top of the picture).
This design can be represented as follows:
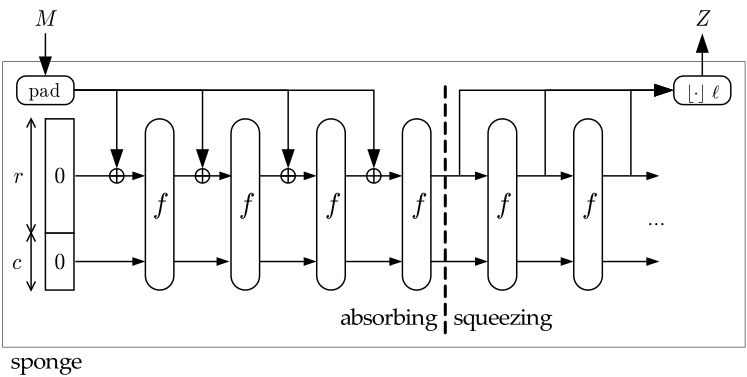
As can be seen from the figure, the scheme consists of two stages:
- Absorbing. The original message M is subject to multi-round permutations f.
- Squeezing. The output of the result of the permutations of the value Z.
The attentive reader must have noticed the letters r and c in the figure. We will not reveal the intrigue ahead of time, say, just by varying the value of these variables, we will get completely different hash functions. So for SHA-512, as these values you need to choose r = 576, c = 1024.
And detail?
So, as I said above, the Keccak algorithm is based on the Sponge design. This means that in order to get the hash, we need to do the following simple steps:
- Take the original message M and add it to the length of the multiple r. Add-on rules captivate with its simplicity. In the form of a formula, they can be represented as follows: M = M || 0x01 || 0x00 || .. || 0x00 || 0x80. Or speaking in Russian, a single byte is added to the message, the required number of zeros and the entire ensemble is completed byte with a value of 0x80.
UPD: All of the above is true only for cases when more than one byte is added. However, if it is necessary to add only one byte, then it suffices to add only 0x81. The error was revealed thanks to the vigilance of the respected OverQuantum . And even earlier, the habswerter fdsc spoke about this, whose post in the sandbox was unnoticed, but now justice has triumphed. Thus, the code must be rewritten with this remark! - Then for each block M i with the length r of bits we execute:
- Addition modulo 2 with the first r-bits of the set of initial states S. Before the function starts, all elements of S will be equal to zero.
- N times apply to the resulting data function f. The set of initial states S for block M i + 1 will be the result of the last round of block M i .
- After all the blocks M i have finished, take the final result and return it as a hash value.
Anyway, nothing is clear!
Well, now all the ins and outs of the algorithm with
But first we tear off the covers from the mystery and tell you why we need the parameters r and c.
To do this, we need to say that the Keccak hash function is implemented in such a way that the user can select the permutation function f applied to each M i block from the set of predefined functions b = {f-25, f-50, f-100, f -200, f-400, f-800, f-1600}.
In order for your implementation to use, say, the f-800 function, it is necessary to choose r and c such that the equality r + c = 800 holds.
In addition, by changing the values of r and c, you thereby change the number of rounds of your hash function. Since the number of these is calculated by the formula n = 12 + 2l, where 2 l = (b / 25). So for b = 1600, the number of rounds is 24.
However, although the user has the right to choose for his implementation any of the functions proposed by the authors, it should be noted that only the Keccak-1600 function is accepted as the SHA-3 standard and the authors strongly recommend using it only. So, the authors chose the following parameters as basic values for hashes of different lengths:
')
SHA-224: r = 1156, c = 448 (return the first 28 bytes of the result)
SHA-256: r = 1088, c = 512 (return the first 32 bytes of the result)
SHA-384: r = 832, c = 768 (return the first 48 bytes of the result)
SHA-512: r = 576, c = 1024 (return the first 64 bytes of the result)
And where is the code?
And after all these clarifications, you can go directly to the pseudocode of the algorithm.
The absorbing stage can be represented as the following function:
Keccak-f[b](A) { forall i in 0…nr-1 A = Round[b](A, RC[i]) return A } Here b is the value of the selected function (default 1600). And the function Round () is a pseudo-random permutation applied at each round. The number of rounds nr is calculated from the values of r and c.
The operations performed on each round are the following function:
Round[b](A,RC) { θ step for(int x=0; x<5; x++) C[x] = A[x,0] xor A[x,1] xor A[x,2] xor A[x,3] xor A[x,4]; for(int x=0; x<5; x++) D[x] = C[x-1] xor rot(C[x+1],1); for(int x=0; x<5; x++) A[x,y] = A[x,y] xor D[x]; ρ and π steps for(int x=0; x<5; x++) for(int y=0; y<5; y++) B[y,2*x+3*y] = rot(A[x,y], r[x,y]); χ step for(int x=0; x<5; x++) for(int y=0; y<5; y++) A[x,y] = B[x,y] xor ((not B[x+1,y]) and B[x+2,y]); ι step A[0,0] = A[0,0] xor RC return A } It consists of 4 steps on each of which a series of logical operations are performed on the input data.
Here the function rot (X, n) denotes the cyclic shift of an element X by n positions.
The r [] array is a predefined set of values that indicates how many bytes need to be shifted at each round. The value of all elements of this array is shown in the table below:

The RC array is a set of constants that are also predefined:

The Keccak function itself is the following:
Keccak[r,c](M) { Initialization and padding for(int x=0; x<5; x++) for(int y=0; y<5; y++) S[x,y] = 0; P = M || 0x01 || 0x00 || … || 0x00; P = P xor (0x00 || … || 0x00 || 0x80); //Absorbing phase forall block Pi in P for(int x=0; x<5; x++) for(int y=0; y<5; y++) S[x,y] = S[x,y] xor Pi[x+5*y]; S = Keccak-f[r+c](S); //Squeezing phase Z = empty string; do { for(int x=0; x<5; x++) for(int y=0; y<5; y++) if((x+5y)<r/w) Z = Z || S[x,y]; S = Keccak-f[r+c](S) } while output is requested return Z; } At the Absorbig stage, the hash value is calculated.
And at the Squeezing stage, displaying the results until the required hash length is reached.
Under the spoiler is a small class written in C # that implements all these actions.
public class Keccack { // , 24 // ι private ulong[] RC ={0x0000000000000001, 0x0000000000008082, 0x800000000000808A, 0x8000000080008000, 0x000000000000808B, 0x0000000080000001, 0x8000000080008081, 0x8000000000008009, 0x000000000000008A, 0x0000000000000088, 0x0000000080008009, 0x000000008000000A, 0x000000008000808B, 0x800000000000008B, 0x8000000000008089, 0x8000000000008003, 0x8000000000008002, 0x8000000000000080, 0x000000000000800A, 0x800000008000000A, 0x8000000080008081, 0x8000000000008080, 0x0000000080000001, 0x8000000080008008}; // , θ private int[,] r = {{0, 36, 3, 41, 18} , {1, 44, 10, 45, 2} , {62, 6, 43, 15, 61} , {28, 55, 25, 21, 56} , {27, 20, 39, 8, 14} }; private int w, l, n; // b=1600 public Keccack(int b) { w = b / 25; l = (Convert.ToInt32(Math.Log(w, 2))); n = 12 + 2 * l; } // x n private ulong rot(ulong x, int n) { n = n % w; return (((x << n) | (x >> (w - n)))); } private ulong[,] roundB(ulong[,] A, ulong RC) { ulong[] C = new ulong[5]; ulong[] D = new ulong[5]; ulong[,] B = new ulong[5, 5]; // θ for (int i = 0; i < 5; i++) C[i] = A[i, 0] ^ A[i, 1] ^ A[i, 2] ^ A[i, 3] ^ A[i, 4]; for (int i = 0; i < 5; i++) D[i] = C[(i + 4) % 5] ^ rot(C[(i + 1) % 5], 1); for (int i = 0; i < 5; i++) for (int j = 0; j < 5; j++) A[i, j] = A[i, j] ^ D[i]; // ρ π for (int i = 0; i < 5; i++) for (int j = 0; j < 5; j++) B[j, (2 * i + 3 * j) % 5] = rot(A[i, j], r[i, j]); // χ for (int i = 0; i < 5; i++) for (int j = 0; j < 5; j++) A[i, j] = B[i, j] ^ ((~B[(i + 1) % 5, j]) & B[(i + 2) % 5, j]); // ι A[0, 0] = A[0, 0] ^ RC; return A; } private ulong[,] Keccackf(ulong[,] A) { for (int i = 0; i < n; i++) A = roundB(A, RC[i]); return A; } // 16- r- 64- private ulong[][] padding(string M, int r) { int size = 0; // r M = M + "01"; while (((M.Length / 2) * 8 % r) != ((r - 8))) { M = M + "00"; } ; M = M + "80"; // b- size = (((M.Length / 2) * 8) / r); // 64- ulong[][] arrayM = new ulong[size][]; arrayM[0] = new ulong[1600 / w]; string temp = ""; int count = 0; int j = 0; int i = 0; // 64- foreach (char ch in M) { if (j > (r/w-1)) { j = 0; i++; arrayM[i] = new ulong[1600 / w]; } count++; if ((count * 4 % w) == 0) { arrayM[i][j] = Convert.ToUInt64(M.Substring((count - w / 4), w / 4), 16); temp = ToReverseHexString(arrayM[i][j]); arrayM[i][j] = Convert.ToUInt64(temp, 16); j++; } } return arrayM; } private string ToReverseHexString(ulong S) { string temp = BitConverter.ToString(BitConverter.GetBytes(S).ToArray()).Replace("-", ""); return temp; } private string ToHexString(ulong S) { string temp = BitConverter.ToString(BitConverter.GetBytes(S).Reverse().ToArray()).Replace("-", ""); return temp; } // public string GetHash(string M, int r, int c, int d) { // S=0 ulong[,] S = new ulong[5, 5]; for (int i = 0; i < 5; i++) for (int j = 0; j < 5; j++) S[i, j] = 0; ulong[][] P = padding(M, r); // P Pi, // 64- foreach (ulong[] Pi in P) { for (int i = 0; i < 5; i++) for (int j = 0; j < 5; j++) if((i + j * 5)<(r/w)) S[i, j] = S[i, j] ^ Pi[i + j * 5]; Keccackf(S); } string Z = ""; // , do { for (int i = 0; i < 5; i++) for (int j = 0; j < 5; j++) if ((5*i + j) < (r / w)) Z = Z + ToReverseHexString(S[j, i]); Keccackf(S); } while (Z.Length < d*2); return Z.Substring(0, d * 2); } } You can download the source from here.
PS All materials and illustrations for this article were found on the official website of the Keccak hash function.
UPD: fshp kindly shared a link to the Russian-language description of the main features of the new standard.
UPD2: after publishing the articles the reader with the nickname Admiral addressed me in the mail. He proposed more optimized code that does not use work with strings.
Admiral reader implementation
using System; using System.Linq; using System.Collections.Generic; class Program { /*const */ static private Byte InstanceNumber = 6; /*const */ static private UInt16[] b_array = { 25, 50, 100, 200, 400, 800, 1600 }; //permutation_width /*const */ static private Byte matrixSize = 5 * 5; /*const */ static private Byte[] w_array = { 1, 2, 4, 8, 16, 32, 64 }; //b / 25; /*const */ static private Byte[] l_array = { 0, 1, 2, 3, 4, 5, 6 }; //log(static_cast<float>(m_w)) / log(2.0F) /*const */ static private Byte[] n_array = { 12, 14, 16, 18, 20, 22, 24 }; //12 + 2 * l -> number_of_permutation /*const */ static private Byte[,] r = { {0, 36, 3, 41, 18}, {1, 44, 10, 45, 2}, {62, 6, 43, 15, 61}, {28, 55, 25, 21, 56}, {27, 20, 39, 8, 14} }; /*const */ static private UInt64[] RC = {//24 by w_array[KeccakInstanceCount - 1] (for 1600), for less please use less in w_array 0x0000000000000001, 0x0000000000008082, 0x800000000000808A, 0x8000000080008000, 0x000000000000808B, 0x0000000080000001, 0x8000000080008081, 0x8000000000008009, 0x000000000000008A, 0x0000000000000088, 0x0000000080008009, 0x000000008000000A, 0x000000008000808B, 0x800000000000008B, 0x8000000000008089, 0x8000000000008003, 0x8000000000008002, 0x8000000000000080, 0x000000000000800A, 0x800000008000000A, 0x8000000080008081, 0x8000000000008080, 0x0000000080000001, 0x8000000080008008 }; static private UInt64[,] B = new UInt64[5, 5]; static private UInt64[] C = new UInt64[5]; static private UInt64[] D = new UInt64[5]; /*const*/ static public UInt16[] rate_array = { 576, 832, 1024, 1088, 1152, 1216, 1280, 1344, 1408 }; /*const*/ static public UInt16[] capacity_array = { 1024, 768, 576, 512, 448, 384, 320, 256, 192 }; public enum SHA3 { SHA512 = 0, SHA384, SHA256 = 3, SHA224 }; static private UInt64[,] Keccak_f(UInt64[,] A) { for(Byte i = 0; i < n_array[InstanceNumber]; i++) A = Round(A, RC[i]); return A; } static private UInt64[,] Round(UInt64[,] A, UInt64 RC_i) { Byte i, j; //theta step for (i = 0; i < 5; i++) C[i] = A[i,0] ^ A[i,1] ^ A[i,2] ^ A[i,3] ^ A[i,4]; for (i = 0; i < 5; i++) D[i] = C[(i + 4) % 5] ^ ROT(C[(i + 1) % 5], 1, w_array[InstanceNumber]); for (i = 0; i < 5; i++) for (j = 0; j < 5; j++) A[i,j] = A[i,j] ^ D[i]; //rho and pi steps for (i = 0; i < 5; i++) for (j = 0; j < 5; j++) B[j,(2 * i + 3 * j) % 5] = ROT(A[i,j], r[i,j], w_array[InstanceNumber]); //chi step for (i = 0; i < 5; i++) for (j = 0; j < 5; j++) A[i,j] = B[i,j] ^ ((~B[(i + 1) % 5,j]) & B[(i + 2) % 5,j]); //iota step A[0,0] = A[0,0] ^ RC_i; return A; } static private UInt64 ROT(UInt64 x, Byte n, Byte w) { return ((x << (n % w)) | (x >> (w - (n % w)))); } static private Byte[] Keccak(UInt16 rate, UInt16 capacity, List<Byte> Message) { //Padding Message.Add(0x01); UInt16 min = (UInt16)((rate - 8) / 8); UInt16 n = (UInt16)Math.Truncate((Double)(Message.Count / min)); UInt32 messageFullCount = 0; if (n < 2) { messageFullCount = min; } else { messageFullCount = (UInt32)(n * min + (n - 1)); } UInt32 delta = (UInt32)(messageFullCount - Message.Count); if ((Message.Count + delta) > UInt16.MaxValue - 1) throw (new Exception("Message might be too large")); /*Byte[] byteArrayToAdd = new Byte[delta]; Message.AddRange(byteArrayToAdd);*/ while (delta > 0) { Message.Add(0x00); delta--; } if ((Message.Count * 8 % rate) != (rate - 8)) throw (new Exception("Length was incorect calculated")); Message.Add(0x80); /*const*/ Int32 size = (Message.Count * 8) / rate; UInt64[] P = new UInt64[size * matrixSize]; Int32 xF = 0, count = 0; Byte i = 0, j = 0; for(xF = 0; xF < Message.Count; xF++) { if (j > (rate / w_array[InstanceNumber] - 1)) { j = 0; i++; } count++; if ((count * 8 % w_array[InstanceNumber]) == 0) { P[size * i + j] = ReverseEightBytesAndToUInt64( Message.GetRange(count - w_array[InstanceNumber] / 8, 8).ToArray() ); j++; } } //Initialization UInt64 [,]S = new UInt64[5,5]; for(i = 0; i < 5; i++) for(j = 0; j < 5; j++) S[i,j] = 0; //Absorting phase for(xF = 0; xF < size; xF++) { for(i = 0; i < 5; i++) for(j = 0; j < 5; j++) if ((i + j * 5) < (rate / w_array[InstanceNumber])) { S[i, j] = S[i, j] ^ P[size * xF + i + j * 5]; } Keccak_f(S); } //Squeezing phaze Byte a = 0; Byte d_max = (Byte)(capacity / (2 * 8)); List<Byte> retHash = new List<Byte>(d_max); for( ; ; ) { for(i = 0; i < 5; i++) for(j = 0; j < 5; j++) if((5 * i + j) < (rate / w_array[InstanceNumber])) { if(a >= d_max) i = j = 5; else { retHash.AddRange(FromUInt64ToReverseEightBytes(S[j, i])); a = (Byte)retHash.Count; } } if(a >= d_max) break; Keccak_f(S); } return retHash.GetRange(0, d_max).ToArray(); } static private UInt64 ReverseEightBytesAndToUInt64(Byte[] bVal) { UInt64 ulVal = 0L; for (Byte i = 8, j = 0; i > 0; i--) { ulVal += (UInt64)((bVal[i - 1] & 0xF0) >> 4) * (UInt64)Math.Pow(16.0F, 15 - (j++)); ulVal += (UInt64)(bVal[i - 1] & 0x0F) * (UInt64)Math.Pow(16.0F, 15 - (j++)); } return ulVal; } static private Byte[] FromUInt64ToReverseEightBytes(UInt64 ulVal) { Byte[] bVal = new Byte[8]; Byte a = 0; do { bVal[a] = (Byte)((ulVal % 16) * 1); ulVal = ulVal / 16; bVal[a] += (Byte)((ulVal % 16) * 16); a++; } while (15 < (ulVal = ulVal / 16)); while (a < 8) { bVal[a++] = (Byte)ulVal; ulVal = 0; } return bVal; } static void Main(String[] args) { if (args.Length < 1) return; List<Byte> MessageB; String message = string.Copy(args[0]); MessageB = strToByteList(message); String hash_224 = ByteArrayToString(Keccak(rate_array[(Byte)SHA3.SHA224], capacity_array[(Byte)SHA3.SHA224], MessageB)); MessageB = strToByteList(message); String hash_256 = ByteArrayToString(Keccak(rate_array[(Byte)SHA3.SHA256], capacity_array[(Byte)SHA3.SHA256], MessageB)); MessageB = strToByteList(message); String hash_384 = ByteArrayToString(Keccak(rate_array[(Byte)SHA3.SHA384], capacity_array[(Byte)SHA3.SHA384], MessageB)); MessageB = strToByteList(message); String hash_512 = ByteArrayToString(Keccak(rate_array[(Byte)SHA3.SHA512], capacity_array[(Byte)SHA3.SHA512], MessageB)); Console.WriteLine("Message: " + message + "\r\n" + "Hash_224: " + hash_224 + "\r\n" + "Hash_256: " + hash_256 + "\r\n" + "Hash_384: " + hash_384 + "\r\n" + "Hash_512: " + hash_512 + "\r\n"); } static List<Byte> strToByteList(String str) { List<Byte> ret = new List<byte>(str.Length); foreach(char ch in str) { ret.Add((Byte)ch); } return ret; } static public String ByteArrayToString(Byte[] b) { System.Text.StringBuilder sb = new System.Text.StringBuilder(16); for (Int32 i = 0; i < Math.Min(b.Length, Int32.MaxValue - 1); i++) sb.Append(String.Format("{0:X2}", b[i])); return sb.ToString(); } } Source: https://habr.com/ru/post/159073/
All Articles