Introduction to Pedestrian Modeling
Probably many of them heard about such a direction of research as traffic management. People have been working on this problem for a long time and, as a result, have achieved some success - adequate modeling of urban traffic allows you to significantly ease the unloading of city roads, reduce traffic accidents through optimal placement and adjustment of traffic lights, determine the best options for eliminating traffic jams at the most loaded places.
However, scientists began to seriously address the problem of reliably modeling the behavior of pedestrian flows close to the aforementioned. In this article I will try to acquaint readers with some existing models of pedestrian flows, and talk about their properties and features.
Researchers became interested in this topic at the end of the 80s - the beginning of the 90s of the XX century, after studying the consequences of catastrophes, derailments and accidents revealed deficiencies in the structure of buildings and ships, resulting in significant loss of life. By standards, these constructions met the requirements of inspections, but in an emergency situation unexpected “bottlenecks” opened up, leading to dire consequences. But if it would be possible to simulate human flows moving in the structure under consideration, and to consider their behavior, both in ordinary and in critical situations, the object could be improved and made more secure before construction.
The main problem arising in the simulation of pedestrian traffic is the difficulty of recreating plausible behavior. It is logical that moving, I will strive to reach the destination point (and how? As quickly as possible? Slowly walking?), And trying not to collide with other pedestrians. However, in reality, I do not rarely meet with completely illogical (from my point of view) behavior - sudden stops during heavy traffic, sharp reversals in place, a banal “spring through” ...
There are three different levels of pedestrian behavior.
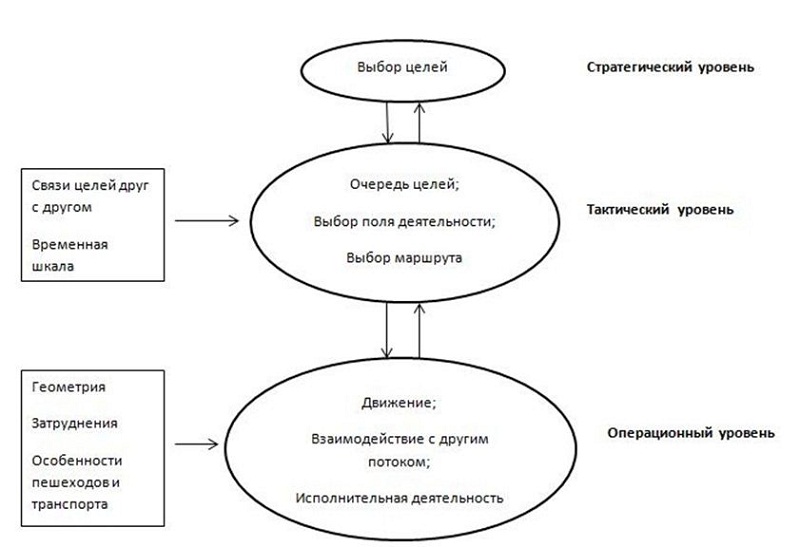
At the strategy level, a pedestrian decides what goals he wants to achieve and in what order he will fulfill them. The tactical level is responsible for the selection of short-term decisions - such as choosing the optimal route in accordance with the terrain and traffic intensity. The level of operations describes directly the movement of a pedestrian, i.e. immediate decisions needed to avoid collisions, etc.
Decision making scheme can be represented as follows:
')
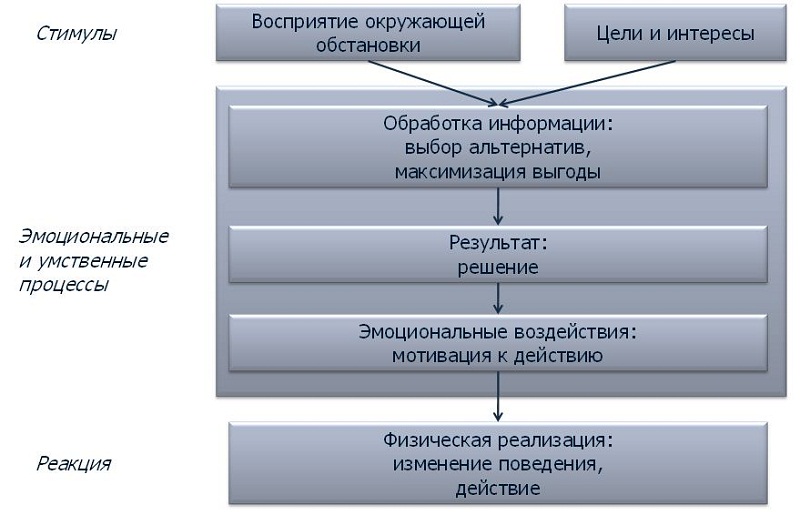
To recreate the believable behavior of the pedestrian flow model, it is necessary to process a large array of information from other disciplines - sociology, psychology, etc. Understanding this information will provide an opportunity to work with the two upper levels of pedestrian behavior. To simulate the operational level, they are often based on various physical models, representing the human flow, for example, as a kind of substance consisting of large molecules or figures on a chessboard field. The purpose of such a presentation is to find such a model that will be as simple to implement as possible, but at the same time it will reproduce the “realistic” behavior of the human stream, which will be close to the experimental results and can be reproduced more than once.
When choosing a model, it is necessary to determine a number of parameters that the model possesses:
• Choice of microscopic or macroscopic model. In the view of the microscopic model, you can select a certain number of pedestrians, determine their characteristics, trace their route. In a macroscopic model it is impossible to single out a separate pedestrian, pedestrian flows are fundamental.
• Discrete or continuous model.
• Deterministic or stochastic model. In the deterministic model, all possible reactions are determined and unchanged. In the stochastic model, a pedestrian may react differently to the same situation.
• Model based on rules or based on forces. In the rule-based model, the decision is made based on the current situation and pedestrian goals. In a model based on forces, a pedestrian “feels” the forces acting on him from other pedestrians and from the infrastructure, the decision is made depending on the size of the resulting amount of the sum of forces acting on a person.
• High or low accuracy. Characterizes the "realism" of the model. The model with a high degree of accuracy will try to implement a flow of traffic with decision-making algorithms as close as possible to reality, a path, etc. A model with a low degree of accuracy may be completely devoid of any intelligence. The first path leads to greater complexity of the model, an increase in the number of variables and, quite likely, an increase in response time, since A large amount of data will be processed. A model with lower accuracy will be easier to implement, work faster, but it must be borne in mind that its accuracy will not be perfect.
Among the existing models of pedestrian flows can be identified:
• Model of attracting forces: in it pedestrians were represented as electric charges that are in a magnetic field. Pedestrians and obstacles are presented as positive charges, and movement targets as negative charges;
• Models that use queuing theory to describe the movement of pedestrians using probabilistic functions;
• Cellular automata: in them the whole space is a grid in which each pedestrian can occupy only one cell. Movement is modeled as the movement of people between cells according to certain rules;
• Gas-kinetic model: here pedestrians are represented as molecules in liquefied gas. The exact speed and position of the pedestrian molecules are unknown, instead, the statistical distribution of particles is known, based on the Boltzmann equation;
• Model of social forces: uses Newtonian mechanics to describe the movement of pedestrians. Forces are generated by social interactions;
• Design models: most of the parameters are calculated once based on data from a practical experiment, tables are drawn up depending on the number of pedestrians and the size of the room. In the future, these data are used to describe the movement of pedestrian flow.
Consider the principles of operation of these models in more detail.
It was developed by Professor S. Okazaki together with S. Matsushita in the late 1970s. It is a microscopic continuous model. According to this model, each pedestrian and obstacle carries a positive charge. The negative charge is concentrated in the place where pedestrians are heading. Pedestrians move to the goal and avoid collisions. Two forces affect each pedestrian. The first is the magnetic force defined in Coulomb's law, which depends on the amount of electric charge of the pedestrian and the distance between the pedestrian and the purpose of his movement.
The second force acts on pedestrians in order to prevent collisions with other pedestrians or obstacles through the use of acceleration.
In fig. 3, acceleration a affects pedestrian A in order to change the RV vector on the direction of the AC line. The AC line is a tangent drawn from pedestrian A to a circle delineated around pedestrian B. This circle is a “personal space zone” and it is undesirable for strangers to violate its boundaries. Its radius depends on cultural peculiarities and in the research of S. Okazaki a circle radius of 60 centimeters was adopted.

Advantages of the model:
• Ease of implementation;
• High speed model.
Disadvantages of the model:
• Impossibility of individualization of a pedestrian (determination of height, weight, etc.);
• Inability to take into account such phenomena as panic, rudeness, emergency situations (when human behavior becomes unpredictable);
• It is impossible to set a different pedestrian behavior, except for the desire to achieve the goal and avoid collisions with other pedestrians or obstacles.
In the theory of queuing, movement is described in terms of probability density functions. Pedestrians arrive with a certain probability in the server, are serviced and stand in a queue. The three main elements in the queuing system are arrival, the serving mechanism and the queuing (i.e. FIFO). Laszlo Lovas proposed a stochastic model where the pedestrian flow in a building can be modeled as a process of organizing a network of queues. In the process, each pedestrian is considered as the only flow object that interacts with other objects. Nodes in the created queue network are rooms, and connections are treated as doors. In the process of movement, a person chooses a new node according to a certain probability, which leads to a new equation that describes the change in the number of pedestrians from time t to the onset of time t + h. From the resulting equation, it is possible to estimate the efficiency of evacuating people from a room (that is, the expected remaining number of people in a site and the expected number of people evacuated).

Cellular automatons are a simple and fast way to simulate a pedestrian flow. In the cellular model of automata, the whole space is a grid.
Each grid cell can be occupied by a single pedestrian. The movement is modeled as a change of cells, where several rules are applied to automata (pedestrians). These sets of rules differ in different implementations of this model. Some implementations of the model will be discussed further.
Blue and Adler identified two elements of foot traffic: moving forward and resolving conflicts. Moving forward indicates a pedestrian’s desire to achieve a certain goal and comes down to determining the speed and acceleration of each pedestrian. Conflict resolution means the desire to avoid physical contact.
The set of rules proposed by Bleu and Adler consists of six rules that apply at four different stages. The first step applies route change rules. At the second stage, all pedestrians are assigned a new cell. At the third stage, promotion rules are applied for each pedestrian. At the last stage, pedestrians jump into new cells.
Changing the route in this model is governed by five rules. Change is possible only if the adjacent cell is accessible and not occupied by a pedestrian.
1. Determine whether cells are available directly to the right and left.
2. The solution is controversial if the adjacent cell is available, but there are two routes to this cell. At this stage, randomly determine which pedestrian will gain access to the cage.
3. Complete the re-routing if both adjacent cells are unavailable.
4. Calculate unallocated distance for active and unoccupied adjacent routes. If the distance is unique and maximum, assign a pedestrian to this route. This means that a pedestrian will choose a path that does not have any contradictions on the largest possible plot. If no unique maximum distance is found, assign a route according to rule five.
5. If the three routes lead to the maximum distance, a separation of 80/10/10 is applied for the current route and two adjacent routes. If two routes lead to the maximum distance, a 50/50 split is applied.
After determining the route, the pedestrian moves along the route assigned to it. This is done in the second stage. At the third stage, the pedestrians are assigned the speed of movement. During this stage, pedestrians may change places with a certain probability. This can happen if two pedestrians move on each other. At stage four, all pedestrians move.
The model was applied to unidirectional pedestrian alleys and bidirectional flow, in which the number of pedestrians moving in one direction is much greater than pedestrians moving in the opposite direction.
Dijkstra, Jessurun and Timmermans proposed a model with a focus on moving pedestrians in the alley. During the movement of a pedestrian, there are four steps:
1. Check if the pedestrian passed the decision (end of action or base network node). If this is true, go to step three. Otherwise, go to step two.
2. If the pedestrian is in the solution cell (network node), examine the behavior of the pedestrian and turn the pedestrian in the desired direction. Thus, the decision will be made.
3. If the newly selected cell is empty, move the pedestrian to the cell. Otherwise, proceed to step four.
4. If the cell to the left or to the right is not occupied, move to the left or to the right.
In this model, the movement is directed toward the goal and changed only at the moments of decision making. Interaction with other pedestrians was not considered.
Yang Lizhong et al. Developed a model of cellular fire-fighting automata. They presented special rules for calculating the route in case of fire (degree of danger). This degree of danger consists of the degree of danger of the position (a certain distance to the closest exit) and the degree of danger of fire (a certain distance to the fire). In their model, three stages are defined.
1. Each pedestrian chooses a cell with the smallest degree of danger, relative to his own view. If all adjacent cells are occupied or have a higher degree of danger, the resident does not move.
2. If more than one resident wants to move to the same cell, one of the applicants is chosen randomly. The rest at this stage should be expected.
3. Each resident updates the degree of danger.
Pedestrian dynamics have some obvious similarities with fluids. For example, the movement around obstacles is very similar to the “fluid flow” around an obstacle. Motion in intermediate density is limited (short-term correlations). It is therefore not surprising that, as for transport dynamics, the earliest models of pedestrian dynamics took inspiration from hydrodynamics or gas-kinetic theory. Usually these macroscopic models are deterministic, based on the interaction of forces and are models of low accuracy.
Henderson tried to draw an analogy between large concentrations of people and classic gas. As a result of tracking the movement in various crowds under the condition of low density ("gasiness"), he found the correspondence of the velocity distribution functions to the Maxwell-Boltzmann distribution.
Encouraged by this observation, he later developed a fluid-dynamic theory of pedestrian flow. When describing interactions between pedestrians as a series of collisions in which particles exchange impulses and energy, a homogeneous crowd can be described by the kinetic theory of gases. However, the interpretation of quantities is not completely clear. For example, analogs of pressure and temperature are in the context of pedestrian traffic. The temperature can be correlated with the speed difference, which is associated with the distribution of the required speeds, while the pressure expresses the requirement to move against the force in a certain direction.
Gas-kinetic models have problems with low pedestrian density, which is a common problem for all macroscopic models.
The model of social forces was developed by Helbing and Molnar. In this model, the various motivations and influences of a pedestrian are described by various kinds of power. This model is based mainly on Newtonian dynamics, but the mass is equal to 1. This leads to a module for forces. This model is able to recreate several natural phenomena that occur during pedestrian movement:
1. Pedestrians usually choose the fastest route;
2. Pedestrians move at an individual speed, taking into account the situation, gender, age, environment, etc. The speed is a Gaussian distribution.
Consider the forces and parameters used in this model (I will give a description without a mathematical apparatus, because the article is still more overview):
1) The most obvious force is the so-called driving force, which reflects the pedestrian's motivation to move to the target at the required speed.
2) The most important interaction between pedestrians is the desire to maintain a certain distance to other pedestrians. To describe this behavior, repulsion is implemented in the model of social forces. The repulsion - depending on the distance between pedestrians - it has the highest value at a close distance (but not outside the maximum limit) and tends to zero with increasing distance between pedestrians. This can be implemented using an exponential function, resulting in a force describing interactions between pedestrians.
3) Normally, walking is anisotropic. This means that actions in front of a pedestrian are more important than actions that occur behind him. People have the ability to anticipate the actions of other people, and thus they can respond to actions taken by other people. To realize this in the model of social forces, actions that occur in the field of view of a pedestrian must have a greater degree of influence than actions of pedestrians produced by all fields of view. To describe this behavior, the form factor of the field of view is implemented in such a way that it depends on the angle between the desired direction of movement and the direction of the pedestrian exhibiting repulsive force.

If lambda is less than 1, then pedestrian traffic can be considered as anisotropic - pedestrians will not respond equally to objects. Objects in front have a greater impact on behavior than side or behind a pedestrian.
4) The sliding friction force is a result of the fact that pedestrians try to avoid collisions with other pedestrians who move at high speed at short distances.
5) Attractors can influence the behavior of pedestrians. Windows or special attractors for example can attract a pedestrian, and he will move to the attractor, and some (fire, warning sign) - to scare. The attractiveness of the attractor is time-dependent and decreases linearly to zero. Attractors can be modeled in the same way as social power between pedestrians
6) Pedestrians often walk in groups. After they are separated (for example, if pedestrians must avoid a collision with an obstacle), individual pedestrians try to convert the group again. This is carried out under the influence of the force of attraction acting from pedestrian A to pedestrian B.
7) All pedestrians are characterized by individual behavior, and thus their movement may differ from the adopted laws. This behavior is represented by oscillation. Oscillations are normally distributed and perpendicular to the vector pointing to the desired direction.
The model of social forces consists of a large number of forces that represent various influences that affect a pedestrian in reality. The sum of all forces describes the movement and direction of a pedestrian.
Depending on the simulated case, all forces need not be considered (for example, physical strength can be neglected if no process of panic or evacuation is simulated).
By the way, it is the model of social forces that is used to simulate pedestrian flows in PTV VISION VISSIM.
The use of computational models implies a large-scale experiment involving a large number of people in order to identify patterns of change in the parameters of the pedestrian flow (its speed, density, etc.) depending on the surrounding conditions.
In Russia, so to say, for “official modeling” you can use GOST 12.1.004-91 “Fire safety. General requirements ", which is based on the calculation method with the representation of the pedestrian flow, just as it was done in the gas-kinetic model. This GOST only gives an approximate idea of the effectiveness of the configuration layout.
GOST 12.1.004-91 has many drawbacks, such as:
• Great dependence on predetermined values (only 3 variants of the average density of the horizontal projection of a person are considered - an adult, an adult in winter clothes, a teenager;
• It does not take into account the fact that the physique of people can vary greatly;
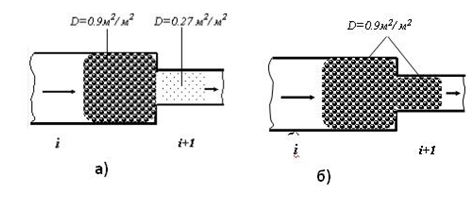
• Low modeling accuracy (for example, decompression of the human flow is not taken into account, see the figure below);
• Focus only on fire safety.
Where a) the real decompression of the pedestrian flow, and b) according to GOST 12.1.004-91.
On this I would like to finish this article. This topic is quite large and interesting, and I did not consciously touch upon mathematics. The article would have swelled at least one and a half times, and for the introductory article and the current version was quite voluminous. At the moment, there are practically no publications in Russian devoted to this topic, and if my article arouses interest, then I will be just glad.
However, scientists began to seriously address the problem of reliably modeling the behavior of pedestrian flows close to the aforementioned. In this article I will try to acquaint readers with some existing models of pedestrian flows, and talk about their properties and features.
Researchers became interested in this topic at the end of the 80s - the beginning of the 90s of the XX century, after studying the consequences of catastrophes, derailments and accidents revealed deficiencies in the structure of buildings and ships, resulting in significant loss of life. By standards, these constructions met the requirements of inspections, but in an emergency situation unexpected “bottlenecks” opened up, leading to dire consequences. But if it would be possible to simulate human flows moving in the structure under consideration, and to consider their behavior, both in ordinary and in critical situations, the object could be improved and made more secure before construction.
The main problem arising in the simulation of pedestrian traffic is the difficulty of recreating plausible behavior. It is logical that moving, I will strive to reach the destination point (and how? As quickly as possible? Slowly walking?), And trying not to collide with other pedestrians. However, in reality, I do not rarely meet with completely illogical (from my point of view) behavior - sudden stops during heavy traffic, sharp reversals in place, a banal “spring through” ...
There are three different levels of pedestrian behavior.

At the strategy level, a pedestrian decides what goals he wants to achieve and in what order he will fulfill them. The tactical level is responsible for the selection of short-term decisions - such as choosing the optimal route in accordance with the terrain and traffic intensity. The level of operations describes directly the movement of a pedestrian, i.e. immediate decisions needed to avoid collisions, etc.
Decision making scheme can be represented as follows:
')

To recreate the believable behavior of the pedestrian flow model, it is necessary to process a large array of information from other disciplines - sociology, psychology, etc. Understanding this information will provide an opportunity to work with the two upper levels of pedestrian behavior. To simulate the operational level, they are often based on various physical models, representing the human flow, for example, as a kind of substance consisting of large molecules or figures on a chessboard field. The purpose of such a presentation is to find such a model that will be as simple to implement as possible, but at the same time it will reproduce the “realistic” behavior of the human stream, which will be close to the experimental results and can be reproduced more than once.
When choosing a model, it is necessary to determine a number of parameters that the model possesses:
• Choice of microscopic or macroscopic model. In the view of the microscopic model, you can select a certain number of pedestrians, determine their characteristics, trace their route. In a macroscopic model it is impossible to single out a separate pedestrian, pedestrian flows are fundamental.
• Discrete or continuous model.
• Deterministic or stochastic model. In the deterministic model, all possible reactions are determined and unchanged. In the stochastic model, a pedestrian may react differently to the same situation.
• Model based on rules or based on forces. In the rule-based model, the decision is made based on the current situation and pedestrian goals. In a model based on forces, a pedestrian “feels” the forces acting on him from other pedestrians and from the infrastructure, the decision is made depending on the size of the resulting amount of the sum of forces acting on a person.
• High or low accuracy. Characterizes the "realism" of the model. The model with a high degree of accuracy will try to implement a flow of traffic with decision-making algorithms as close as possible to reality, a path, etc. A model with a low degree of accuracy may be completely devoid of any intelligence. The first path leads to greater complexity of the model, an increase in the number of variables and, quite likely, an increase in response time, since A large amount of data will be processed. A model with lower accuracy will be easier to implement, work faster, but it must be borne in mind that its accuracy will not be perfect.
Among the existing models of pedestrian flows can be identified:
• Model of attracting forces: in it pedestrians were represented as electric charges that are in a magnetic field. Pedestrians and obstacles are presented as positive charges, and movement targets as negative charges;
• Models that use queuing theory to describe the movement of pedestrians using probabilistic functions;
• Cellular automata: in them the whole space is a grid in which each pedestrian can occupy only one cell. Movement is modeled as the movement of people between cells according to certain rules;
• Gas-kinetic model: here pedestrians are represented as molecules in liquefied gas. The exact speed and position of the pedestrian molecules are unknown, instead, the statistical distribution of particles is known, based on the Boltzmann equation;
• Model of social forces: uses Newtonian mechanics to describe the movement of pedestrians. Forces are generated by social interactions;
• Design models: most of the parameters are calculated once based on data from a practical experiment, tables are drawn up depending on the number of pedestrians and the size of the room. In the future, these data are used to describe the movement of pedestrian flow.
Consider the principles of operation of these models in more detail.
1. Model of attracting forces (Magnetic force model)
It was developed by Professor S. Okazaki together with S. Matsushita in the late 1970s. It is a microscopic continuous model. According to this model, each pedestrian and obstacle carries a positive charge. The negative charge is concentrated in the place where pedestrians are heading. Pedestrians move to the goal and avoid collisions. Two forces affect each pedestrian. The first is the magnetic force defined in Coulomb's law, which depends on the amount of electric charge of the pedestrian and the distance between the pedestrian and the purpose of his movement.
The second force acts on pedestrians in order to prevent collisions with other pedestrians or obstacles through the use of acceleration.
In fig. 3, acceleration a affects pedestrian A in order to change the RV vector on the direction of the AC line. The AC line is a tangent drawn from pedestrian A to a circle delineated around pedestrian B. This circle is a “personal space zone” and it is undesirable for strangers to violate its boundaries. Its radius depends on cultural peculiarities and in the research of S. Okazaki a circle radius of 60 centimeters was adopted.

Advantages of the model:
• Ease of implementation;
• High speed model.
Disadvantages of the model:
• Impossibility of individualization of a pedestrian (determination of height, weight, etc.);
• Inability to take into account such phenomena as panic, rudeness, emergency situations (when human behavior becomes unpredictable);
• It is impossible to set a different pedestrian behavior, except for the desire to achieve the goal and avoid collisions with other pedestrians or obstacles.
2. Queuing model
In the theory of queuing, movement is described in terms of probability density functions. Pedestrians arrive with a certain probability in the server, are serviced and stand in a queue. The three main elements in the queuing system are arrival, the serving mechanism and the queuing (i.e. FIFO). Laszlo Lovas proposed a stochastic model where the pedestrian flow in a building can be modeled as a process of organizing a network of queues. In the process, each pedestrian is considered as the only flow object that interacts with other objects. Nodes in the created queue network are rooms, and connections are treated as doors. In the process of movement, a person chooses a new node according to a certain probability, which leads to a new equation that describes the change in the number of pedestrians from time t to the onset of time t + h. From the resulting equation, it is possible to estimate the efficiency of evacuating people from a room (that is, the expected remaining number of people in a site and the expected number of people evacuated).
3. Cellular automata (Cellular automata model)

Cellular automatons are a simple and fast way to simulate a pedestrian flow. In the cellular model of automata, the whole space is a grid.
Each grid cell can be occupied by a single pedestrian. The movement is modeled as a change of cells, where several rules are applied to automata (pedestrians). These sets of rules differ in different implementations of this model. Some implementations of the model will be discussed further.
Blue and Adler identified two elements of foot traffic: moving forward and resolving conflicts. Moving forward indicates a pedestrian’s desire to achieve a certain goal and comes down to determining the speed and acceleration of each pedestrian. Conflict resolution means the desire to avoid physical contact.
The set of rules proposed by Bleu and Adler consists of six rules that apply at four different stages. The first step applies route change rules. At the second stage, all pedestrians are assigned a new cell. At the third stage, promotion rules are applied for each pedestrian. At the last stage, pedestrians jump into new cells.
Changing the route in this model is governed by five rules. Change is possible only if the adjacent cell is accessible and not occupied by a pedestrian.
1. Determine whether cells are available directly to the right and left.
2. The solution is controversial if the adjacent cell is available, but there are two routes to this cell. At this stage, randomly determine which pedestrian will gain access to the cage.
3. Complete the re-routing if both adjacent cells are unavailable.
4. Calculate unallocated distance for active and unoccupied adjacent routes. If the distance is unique and maximum, assign a pedestrian to this route. This means that a pedestrian will choose a path that does not have any contradictions on the largest possible plot. If no unique maximum distance is found, assign a route according to rule five.
5. If the three routes lead to the maximum distance, a separation of 80/10/10 is applied for the current route and two adjacent routes. If two routes lead to the maximum distance, a 50/50 split is applied.
After determining the route, the pedestrian moves along the route assigned to it. This is done in the second stage. At the third stage, the pedestrians are assigned the speed of movement. During this stage, pedestrians may change places with a certain probability. This can happen if two pedestrians move on each other. At stage four, all pedestrians move.
The model was applied to unidirectional pedestrian alleys and bidirectional flow, in which the number of pedestrians moving in one direction is much greater than pedestrians moving in the opposite direction.
Dijkstra, Jessurun and Timmermans proposed a model with a focus on moving pedestrians in the alley. During the movement of a pedestrian, there are four steps:
1. Check if the pedestrian passed the decision (end of action or base network node). If this is true, go to step three. Otherwise, go to step two.
2. If the pedestrian is in the solution cell (network node), examine the behavior of the pedestrian and turn the pedestrian in the desired direction. Thus, the decision will be made.
3. If the newly selected cell is empty, move the pedestrian to the cell. Otherwise, proceed to step four.
4. If the cell to the left or to the right is not occupied, move to the left or to the right.
In this model, the movement is directed toward the goal and changed only at the moments of decision making. Interaction with other pedestrians was not considered.
Yang Lizhong et al. Developed a model of cellular fire-fighting automata. They presented special rules for calculating the route in case of fire (degree of danger). This degree of danger consists of the degree of danger of the position (a certain distance to the closest exit) and the degree of danger of fire (a certain distance to the fire). In their model, three stages are defined.
1. Each pedestrian chooses a cell with the smallest degree of danger, relative to his own view. If all adjacent cells are occupied or have a higher degree of danger, the resident does not move.
2. If more than one resident wants to move to the same cell, one of the applicants is chosen randomly. The rest at this stage should be expected.
3. Each resident updates the degree of danger.
4. Gas kinetic model (Gas-kinetic model)
Pedestrian dynamics have some obvious similarities with fluids. For example, the movement around obstacles is very similar to the “fluid flow” around an obstacle. Motion in intermediate density is limited (short-term correlations). It is therefore not surprising that, as for transport dynamics, the earliest models of pedestrian dynamics took inspiration from hydrodynamics or gas-kinetic theory. Usually these macroscopic models are deterministic, based on the interaction of forces and are models of low accuracy.
Henderson tried to draw an analogy between large concentrations of people and classic gas. As a result of tracking the movement in various crowds under the condition of low density ("gasiness"), he found the correspondence of the velocity distribution functions to the Maxwell-Boltzmann distribution.
Encouraged by this observation, he later developed a fluid-dynamic theory of pedestrian flow. When describing interactions between pedestrians as a series of collisions in which particles exchange impulses and energy, a homogeneous crowd can be described by the kinetic theory of gases. However, the interpretation of quantities is not completely clear. For example, analogs of pressure and temperature are in the context of pedestrian traffic. The temperature can be correlated with the speed difference, which is associated with the distribution of the required speeds, while the pressure expresses the requirement to move against the force in a certain direction.
Gas-kinetic models have problems with low pedestrian density, which is a common problem for all macroscopic models.
5. Social force model
The model of social forces was developed by Helbing and Molnar. In this model, the various motivations and influences of a pedestrian are described by various kinds of power. This model is based mainly on Newtonian dynamics, but the mass is equal to 1. This leads to a module for forces. This model is able to recreate several natural phenomena that occur during pedestrian movement:
1. Pedestrians usually choose the fastest route;
2. Pedestrians move at an individual speed, taking into account the situation, gender, age, environment, etc. The speed is a Gaussian distribution.
Consider the forces and parameters used in this model (I will give a description without a mathematical apparatus, because the article is still more overview):
1) The most obvious force is the so-called driving force, which reflects the pedestrian's motivation to move to the target at the required speed.
2) The most important interaction between pedestrians is the desire to maintain a certain distance to other pedestrians. To describe this behavior, repulsion is implemented in the model of social forces. The repulsion - depending on the distance between pedestrians - it has the highest value at a close distance (but not outside the maximum limit) and tends to zero with increasing distance between pedestrians. This can be implemented using an exponential function, resulting in a force describing interactions between pedestrians.
3) Normally, walking is anisotropic. This means that actions in front of a pedestrian are more important than actions that occur behind him. People have the ability to anticipate the actions of other people, and thus they can respond to actions taken by other people. To realize this in the model of social forces, actions that occur in the field of view of a pedestrian must have a greater degree of influence than actions of pedestrians produced by all fields of view. To describe this behavior, the form factor of the field of view is implemented in such a way that it depends on the angle between the desired direction of movement and the direction of the pedestrian exhibiting repulsive force.

If lambda is less than 1, then pedestrian traffic can be considered as anisotropic - pedestrians will not respond equally to objects. Objects in front have a greater impact on behavior than side or behind a pedestrian.
4) The sliding friction force is a result of the fact that pedestrians try to avoid collisions with other pedestrians who move at high speed at short distances.
5) Attractors can influence the behavior of pedestrians. Windows or special attractors for example can attract a pedestrian, and he will move to the attractor, and some (fire, warning sign) - to scare. The attractiveness of the attractor is time-dependent and decreases linearly to zero. Attractors can be modeled in the same way as social power between pedestrians
6) Pedestrians often walk in groups. After they are separated (for example, if pedestrians must avoid a collision with an obstacle), individual pedestrians try to convert the group again. This is carried out under the influence of the force of attraction acting from pedestrian A to pedestrian B.
7) All pedestrians are characterized by individual behavior, and thus their movement may differ from the adopted laws. This behavior is represented by oscillation. Oscillations are normally distributed and perpendicular to the vector pointing to the desired direction.
The model of social forces consists of a large number of forces that represent various influences that affect a pedestrian in reality. The sum of all forces describes the movement and direction of a pedestrian.
Depending on the simulated case, all forces need not be considered (for example, physical strength can be neglected if no process of panic or evacuation is simulated).
By the way, it is the model of social forces that is used to simulate pedestrian flows in PTV VISION VISSIM.
6. Calculation models
The use of computational models implies a large-scale experiment involving a large number of people in order to identify patterns of change in the parameters of the pedestrian flow (its speed, density, etc.) depending on the surrounding conditions.
In Russia, so to say, for “official modeling” you can use GOST 12.1.004-91 “Fire safety. General requirements ", which is based on the calculation method with the representation of the pedestrian flow, just as it was done in the gas-kinetic model. This GOST only gives an approximate idea of the effectiveness of the configuration layout.
GOST 12.1.004-91 has many drawbacks, such as:
• Great dependence on predetermined values (only 3 variants of the average density of the horizontal projection of a person are considered - an adult, an adult in winter clothes, a teenager;
• It does not take into account the fact that the physique of people can vary greatly;
• Low modeling accuracy (for example, decompression of the human flow is not taken into account, see the figure below);
• Focus only on fire safety.

Where a) the real decompression of the pedestrian flow, and b) according to GOST 12.1.004-91.
----------------------------
On this I would like to finish this article. This topic is quite large and interesting, and I did not consciously touch upon mathematics. The article would have swelled at least one and a half times, and for the introductory article and the current version was quite voluminous. At the moment, there are practically no publications in Russian devoted to this topic, and if my article arouses interest, then I will be just glad.
Source: https://habr.com/ru/post/158975/
All Articles