Parallel programming using computational graph
There are applications that are well implemented as a messaging system. Anything can be a message in a broad sense - data blocks, control "signals", etc. The logic consists of the nodes that process messages, and the connections between them. Such a structure is naturally represented by a graph, along the edges of which the messages processed in nodes “flow”. The most well-established name for such a model is a computational graph.
With the help of a computational graph, it is possible to establish dependencies between tasks and, to some extent, programmatically implement the “dataflow architecture”.
In this post I will describe how to implement such a model in C ++ using the Intel Threading Building Blocks library (Intel TBB), namely the class tbb :: flow :: graph.
')
Intel Threading Building Blocks is a C ++ template library for parallel programming. It is distributed free of charge in an open source implementation, but there is also a commercial version. Binary format is available for Windows *, Linux * and OS X *.
In TBB there are many ready-made algorithms, structures and data structures that are “sharpened” for use in parallel computing. In particular, there are constructions that allow to implement the computational graph, which will be discussed.
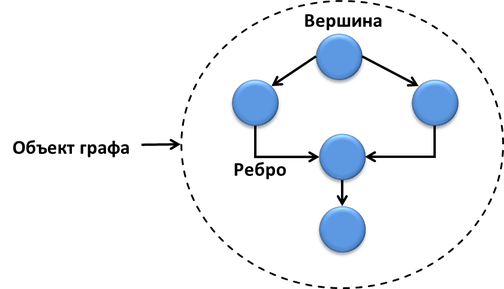
The graph, as is known, consists of vertices (nodes) and edges. The computing graph tbb :: flow :: graph also consists of nodes (node), edges (edges) and an object of the entire graph.
Nodes of the graph have interfaces of the sender and the recipient, control messages or perform some functions. The edges connect the nodes of the graph and are the "channels" of message transfer.
The body of each node is represented by the TBB task and can be executed in parallel with the others, if there are no dependencies between them. In TBB, many parallel (or all) algorithms are built on tasks — small work items (instructions) that are executed by worker threads. There can be dependencies between tasks, they can be dynamically redistributed between threads. Through the use of tasks, you can achieve optimal granularity and load balancing on the CPU, as well as build higher-level parallel constructions based on them - such as tbb :: flow :: graph.
A graph consisting of two vertices connected by one edge, one of which prints “Hello”, and the second one “World” can be schematically represented as:
And in the code it will look like this:
Here an object of the graph g and two nodes of the type continue_node are created - h and w. These nodes receive and transmit a message like continue_msg - internally control message. They are used to build dependency graphs, when the node body is executed only after a message is received from its predecessor.
Each of the continue_node executes some conditionally useful code — the “Hello” and “World” stamp. Nodes are joined by an edge using the make_edge method. Everything, the structure of the computational graph is ready - you can run it for execution by sending it a message using the try_put method. Next, the graph works, and, to make sure that all its tasks are completed, we wait using the wait_for_all method.
Imagine that our program should calculate the expression x 2 + x 3 for x from 1 to 10. Yes, this is not the most difficult computational task, but it is quite suitable for demonstration.
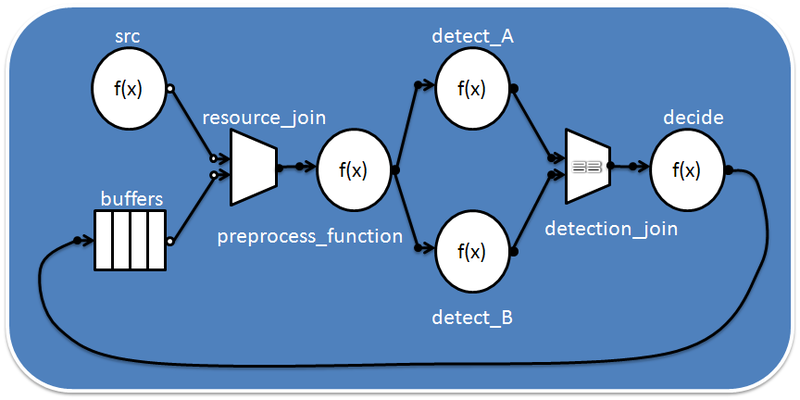
Let's try to present the calculation of the expression in the form of a graph. The first node will take the x values from the incoming data stream and send it to the nodes that are cube and square. The exponentiation operations are independent of each other and can be executed in parallel. To smooth out possible imbalances, they transmit their result to the buffer nodes. Next comes the unifying node that delivers the results of the exponentiation of the summing node, on which the calculation ends:

Code of the graph:
The Sleep (1000) function has been added to visualize the process (example compiled on Windows, use equivalent calls on other platforms). Then everything is like in the first example - we create nodes, combine them with edges and start them for execution. The second parameter in function_node (unlimited or serial) determines how many instances of the node body can be executed in parallel. A node of type join_node determines the readiness of input data / messages at each input, and when both are ready, it sends them to the next node in the form of std :: tuple.
From Wikipedia :
The Problem of the Dining Philosophers is a classic example used in computer science to illustrate synchronization problems in the design of parallel algorithms and techniques for solving these problems.
In the task several philosophers sit at the table, and can either eat or think, but not at the same time. In our version, philosophers eat noodles with chopsticks - to eat you need two sticks, but there is one for each:

In such a situation, a deadlock can occur (for example, if each philosopher grabs his wand, so synchronization of actions between diners is required).
Let's try to present a table with philosophers in the form of tbb :: flow :: graph. Each philosopher will be represented by two nodes: join_node for capturing rods and function_node for accomplishing the “eat” and “think” tasks. Place for the sticks on the table is implemented through queue_node. In queue queue_node can be no more than one stick, and if it is there - it is available for capture. The graph will look like this:

The main function with some constants and header files:
After processing the command line parameters, the library is initialized by creating an object of the type tbb :: task_scheduler_init. This allows you to control the moment of initialization and manually set the number of handler threads. Without this, initialization will take place automatically. Next, create an object of the graph g. The “place for the sticks” queue_node is placed in std :: vector, and in each queue is placed along the stick.
Then philosophers are created in a similar way and placed in std :: vector. The object of each philosopher is transferred to the run function of the graph object. The class philosopher will contain operator (), and the run function allows you to execute this functor in a task that is a child of the root object of the graph object g. So we can wait for the execution of these tasks during the call to g.wait_for_all ().
Class philosopher:
Each philosopher has a name, pointers to the object of the graph and to the left and right sticks, the join_node node, the function_node function node and the my_count counter, counting how many times the philosopher thought and ate.
operator () (), called by the graph's run function, is implemented so that the philosopher thinks first and then attaches himself to the graph.
The make_my_node method creates a functional node, and binds both it and join_node with the rest of the graph:
Note that the graph is created dynamically - the edge is formed using the register_successor method. It is not necessary to first completely create the structure of the graph, and then launch it for execution. In TBB, it is possible to change this structure on the fly, even when the graph is already running — to remove and add new nodes. This adds even more flexibility to the concept of a computational graph.
The node_body class is a simple functor that calls the philosopher :: eat_and_think () method:
The eat_and_think method calls the eat () function and decrements the counter. Then the philosopher puts his wands on the table and thinks. And if he has eaten and has thought the proper number of times, he gets up from the table - he breaks off his join_node connection with the graph by the remove_successor method. Here again, the dynamic structure of the graph is visible - part of the nodes is removed while the rest continue to work.
In our graph there is an edge from queue_node (place for the wand) to the philosopher, or rather its join_node. And in the opposite direction there is no. However, the eat_and_think method can call try_put to put the wand back into the queue.
At the end of the main () function, for each philosopher, the check method is called, which verifies that the philosopher has eaten and thought the correct number of times and does the necessary “cleaning”:
Deadlock in this example does not happen due to the use of join_node. This type of node creates a std :: tuple from the objects received from both inputs. In this case, the input data is not consumed immediately upon receipt. join_node first waits for data to appear on both inputs, then tries to reserve them in turn. If this operation is successful - only then they are “consumed” and std :: tuple is created from them. If the reservation of at least one input “channel” did not work out - those that are already reserved are released. Those. if a philosopher can grab one wand, but the second is busy, he will let go of the first one and wait, without blocking the neighbors in vain.
This example of the dining philosophers demonstrates several possibilities of the TBB graph:
tbb :: flow :: graph provides a fairly wide range of node options. They can be divided into four groups: functional (functional), buffering, combining and dividing, and others. List of node types with symbols:

With the help of the graph implemented in Intel TBB, you can create complex and interesting logic of a parallel program, sometimes called "unstructured parallelism". The computational graph allows you to organize dependencies between tasks, build applications based on the transfer of messages and events.
The structure of the graph can be both static and dynamic - nodes and edges can be added and removed on the fly. You can combine individual subgraphs in a large graph.
Most of the material is based on the English publications of my overseas colleagues.
For those interested, try:
Download Intel Threading Building Blocks Library (Open Source Version):
http://threadingbuildingblocks.org
Commercial version of Intel TBB (not functionally different):
http://software.intel.com/en-us/intel-tbb
English blogs about tbb :: flow :: graph:
http://software.intel.com/en-us/tags/17218
http://software.intel.com/en-us/tags/17455
With the help of a computational graph, it is possible to establish dependencies between tasks and, to some extent, programmatically implement the “dataflow architecture”.
In this post I will describe how to implement such a model in C ++ using the Intel Threading Building Blocks library (Intel TBB), namely the class tbb :: flow :: graph.
')

What is Intel TBB and class tbb :: flow :: graph
Intel Threading Building Blocks is a C ++ template library for parallel programming. It is distributed free of charge in an open source implementation, but there is also a commercial version. Binary format is available for Windows *, Linux * and OS X *.
In TBB there are many ready-made algorithms, structures and data structures that are “sharpened” for use in parallel computing. In particular, there are constructions that allow to implement the computational graph, which will be discussed.
The graph, as is known, consists of vertices (nodes) and edges. The computing graph tbb :: flow :: graph also consists of nodes (node), edges (edges) and an object of the entire graph.

Nodes of the graph have interfaces of the sender and the recipient, control messages or perform some functions. The edges connect the nodes of the graph and are the "channels" of message transfer.
The body of each node is represented by the TBB task and can be executed in parallel with the others, if there are no dependencies between them. In TBB, many parallel (or all) algorithms are built on tasks — small work items (instructions) that are executed by worker threads. There can be dependencies between tasks, they can be dynamically redistributed between threads. Through the use of tasks, you can achieve optimal granularity and load balancing on the CPU, as well as build higher-level parallel constructions based on them - such as tbb :: flow :: graph.
The easiest dependency graph
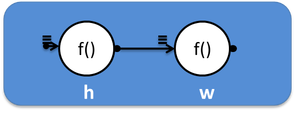
A graph consisting of two vertices connected by one edge, one of which prints “Hello”, and the second one “World” can be schematically represented as:

And in the code it will look like this:
#include <iostream> #include <tbb/flow_graph.h> int main(int argc, char *argv[]) { tbb::flow::graph g; tbb::flow::continue_node< tbb::flow::continue_msg > h( g, []( const tbb::flow::continue_msg & ) { std::cout << "Hello "; } ); tbb::flow::continue_node< tbb::flow::continue_msg > w( g, []( const tbb::flow::continue_msg & ) { std::cout << "World\n"; } ); tbb::flow::make_edge( h, w ); h.try_put(tbb::flow::continue_msg()); g.wait_for_all(); return 0; } Here an object of the graph g and two nodes of the type continue_node are created - h and w. These nodes receive and transmit a message like continue_msg - internally control message. They are used to build dependency graphs, when the node body is executed only after a message is received from its predecessor.
Each of the continue_node executes some conditionally useful code — the “Hello” and “World” stamp. Nodes are joined by an edge using the make_edge method. Everything, the structure of the computational graph is ready - you can run it for execution by sending it a message using the try_put method. Next, the graph works, and, to make sure that all its tasks are completed, we wait using the wait_for_all method.
Simple message passing graph
Imagine that our program should calculate the expression x 2 + x 3 for x from 1 to 10. Yes, this is not the most difficult computational task, but it is quite suitable for demonstration.
Let's try to present the calculation of the expression in the form of a graph. The first node will take the x values from the incoming data stream and send it to the nodes that are cube and square. The exponentiation operations are independent of each other and can be executed in parallel. To smooth out possible imbalances, they transmit their result to the buffer nodes. Next comes the unifying node that delivers the results of the exponentiation of the summing node, on which the calculation ends:

Code of the graph:
#include <tbb/flow_graph.h> #include <windows.h> using namespace tbb::flow; struct square { int operator()(int v) { printf("squaring %d\n", v); Sleep(1000); return v*v; } }; struct cube { int operator()(int v) { printf("cubing %d\n", v); Sleep(1000); return v*v*v; } }; class sum { int &my_sum; public: sum( int &s ) : my_sum(s) {} int operator()( std::tuple<int,int> v ) { printf("adding %d and %d to %d\n", std::get<0>(v), std::get<1>(v), my_sum); my_sum += std::get<0>(v) + std::get<1>(v); return my_sum; } }; int main(int argc, char *argv[]) { int result = 0; graph g; broadcast_node<int> input (g); function_node<int,int> squarer( g, unlimited, square() ); function_node<int,int> cuber( g, unlimited, cube() ); buffer_node<int> square_buffer(g); buffer_node<int> cube_buffer(g); join_node< std::tuple<int,int>, queueing > join(g); function_node<std::tuple<int,int>,int> summer( g, serial, sum(result) ); make_edge( input, squarer ); make_edge( input, cuber ); make_edge( squarer, square_buffer ); make_edge( squarer, input_port<0>(join) ); make_edge( cuber, cube_buffer ); make_edge( cuber, input_port<1>(join) ); make_edge( join, summer ); for (int i = 1; i <= 10; ++i) input.try_put(i); g.wait_for_all(); printf("Final result is %d\n", result); return 0; } The Sleep (1000) function has been added to visualize the process (example compiled on Windows, use equivalent calls on other platforms). Then everything is like in the first example - we create nodes, combine them with edges and start them for execution. The second parameter in function_node (unlimited or serial) determines how many instances of the node body can be executed in parallel. A node of type join_node determines the readiness of input data / messages at each input, and when both are ready, it sends them to the next node in the form of std :: tuple.
Solving the problem of "dining philosophers" with tbb :: flow :: graph
From Wikipedia :
The Problem of the Dining Philosophers is a classic example used in computer science to illustrate synchronization problems in the design of parallel algorithms and techniques for solving these problems.
In the task several philosophers sit at the table, and can either eat or think, but not at the same time. In our version, philosophers eat noodles with chopsticks - to eat you need two sticks, but there is one for each:

In such a situation, a deadlock can occur (for example, if each philosopher grabs his wand, so synchronization of actions between diners is required).
Let's try to present a table with philosophers in the form of tbb :: flow :: graph. Each philosopher will be represented by two nodes: join_node for capturing rods and function_node for accomplishing the “eat” and “think” tasks. Place for the sticks on the table is implemented through queue_node. In queue queue_node can be no more than one stick, and if it is there - it is available for capture. The graph will look like this:

The main function with some constants and header files:
#include <windows.h> #include <tbb/flow_graph.h> #include <tbb/task_scheduler_init.h> using namespace tbb::flow; const char *names[] = { "Archimedes", "Aristotle", "Democritus", "Epicurus", "Euclid", "Heraclitus", "Plato", "Pythagoras", "Socrates", "Thales" }; …. int main(int argc, char *argv[]) { int num_threads = 0; int num_philosophers = 10; if ( argc > 1 ) num_threads = atoi(argv[1]); if ( argc > 2 ) num_philosophers = atoi(argv[2]); if ( num_threads < 1 || num_philosophers < 1 || num_philosophers > 10 ) exit(1); tbb::task_scheduler_init init(num_threads); graph g; printf("\n%d philosophers with %d threads\n\n", num_philosophers, num_threads); std::vector< queue_node<chopstick> * > places; for ( int i = 0; i < num_philosophers; ++i ) { queue_node<chopstick> *qn_ptr = new queue_node<chopstick>(g); qn_ptr->try_put(chopstick()); places.push_back( qn_ptr ); } std::vector< philosopher > philosophers; for ( int i = 0; i < num_philosophers; ++i ) { philosophers.push_back( philosopher( names[i], g, places[i], places[(i+1)%num_philosophers] ) ); g.run( philosophers[i] ); } g.wait_for_all(); for ( int i = 0; i < num_philosophers; ++i ) philosophers[i].check(); return 0; } After processing the command line parameters, the library is initialized by creating an object of the type tbb :: task_scheduler_init. This allows you to control the moment of initialization and manually set the number of handler threads. Without this, initialization will take place automatically. Next, create an object of the graph g. The “place for the sticks” queue_node is placed in std :: vector, and in each queue is placed along the stick.
Then philosophers are created in a similar way and placed in std :: vector. The object of each philosopher is transferred to the run function of the graph object. The class philosopher will contain operator (), and the run function allows you to execute this functor in a task that is a child of the root object of the graph object g. So we can wait for the execution of these tasks during the call to g.wait_for_all ().
Class philosopher:
const int think_time = 1000; const int eat_time = 1000; const int num_times = 10; class chopstick {}; class philosopher { public: typedef queue_node< chopstick > chopstick_buffer; typedef join_node< std::tuple<chopstick,chopstick> > join_type; philosopher( const char *name, graph &the_graph, chopstick_buffer *left, chopstick_buffer *right ) : my_name(name), my_graph(&the_graph), my_left_chopstick(left), my_right_chopstick(right), my_join(new join_type(the_graph)), my_function_node(NULL), my_count(new int(num_times)) {} void operator()(); void check(); private: const char *my_name; graph *my_graph; chopstick_buffer *my_left_chopstick; chopstick_buffer *my_right_chopstick; join_type *my_join; function_node< join_type::output_type, continue_msg > *my_function_node; int *my_count; friend class node_body; void eat_and_think( ); void eat( ); void think( ); void make_my_node(); }; Each philosopher has a name, pointers to the object of the graph and to the left and right sticks, the join_node node, the function_node function node and the my_count counter, counting how many times the philosopher thought and ate.
operator () (), called by the graph's run function, is implemented so that the philosopher thinks first and then attaches himself to the graph.
void philosopher::operator()() { think(); make_my_node(); } think eat : void philosopher::think() { printf("%s thinking\n", my_name ); Sleep(think_time); printf("%s done thinking\n", my_name ); } void philosopher::eat() { printf("%s eating\n", my_name ); Sleep(eat_time); printf("%s done eating\n", my_name ); } The make_my_node method creates a functional node, and binds both it and join_node with the rest of the graph:
void philosopher::make_my_node() { my_left_chopstick->register_successor( input_port<0>(*my_join) ); my_right_chopstick->register_successor( input_port<1>(*my_join) ); my_function_node = new function_node< join_type::output_type, continue_msg >( *my_graph, serial, node_body( *this ) ); make_edge( *my_join, *my_function_node ); } Note that the graph is created dynamically - the edge is formed using the register_successor method. It is not necessary to first completely create the structure of the graph, and then launch it for execution. In TBB, it is possible to change this structure on the fly, even when the graph is already running — to remove and add new nodes. This adds even more flexibility to the concept of a computational graph.
The node_body class is a simple functor that calls the philosopher :: eat_and_think () method:
class node_body { philosopher &my_philosopher; public: node_body( philosopher &p ) : my_philosopher(p) { } void operator()( philosopher::join_type::output_type ) { my_philosopher.eat_and_think(); } }; The eat_and_think method calls the eat () function and decrements the counter. Then the philosopher puts his wands on the table and thinks. And if he has eaten and has thought the proper number of times, he gets up from the table - he breaks off his join_node connection with the graph by the remove_successor method. Here again, the dynamic structure of the graph is visible - part of the nodes is removed while the rest continue to work.
void philosopher::eat_and_think( ) { eat(); --(*my_count); if (*my_count > 0) { my_left_chopstick->try_put( chopstick() ); my_right_chopstick->try_put( chopstick() ); think(); } else { my_left_chopstick->remove_successor( input_port<0>(*my_join) ); my_right_chopstick->remove_successor( input_port<1>(*my_join) ); my_left_chopstick->try_put( chopstick() ); my_right_chopstick->try_put( chopstick() ); } } In our graph there is an edge from queue_node (place for the wand) to the philosopher, or rather its join_node. And in the opposite direction there is no. However, the eat_and_think method can call try_put to put the wand back into the queue.
At the end of the main () function, for each philosopher, the check method is called, which verifies that the philosopher has eaten and thought the correct number of times and does the necessary “cleaning”:
void philosopher::check() { if ( *my_count != 0 ) { printf("ERROR: philosopher %s still had to run %d more times\n", my_name, *my_count); exit(1); } else { printf("%s done.\n", my_name); } delete my_function_node; delete my_join; delete my_count; } Deadlock in this example does not happen due to the use of join_node. This type of node creates a std :: tuple from the objects received from both inputs. In this case, the input data is not consumed immediately upon receipt. join_node first waits for data to appear on both inputs, then tries to reserve them in turn. If this operation is successful - only then they are “consumed” and std :: tuple is created from them. If the reservation of at least one input “channel” did not work out - those that are already reserved are released. Those. if a philosopher can grab one wand, but the second is busy, he will let go of the first one and wait, without blocking the neighbors in vain.
This example of the dining philosophers demonstrates several possibilities of the TBB graph:
- Use join_node to synchronize access to resources
- Dynamic graphing - nodes can be added and removed during operation
- No single points of entry and exit, the graph may have loops
- Using the graph run function
Types of nodes
tbb :: flow :: graph provides a fairly wide range of node options. They can be divided into four groups: functional (functional), buffering, combining and dividing, and others. List of node types with symbols:

Conclusion
With the help of the graph implemented in Intel TBB, you can create complex and interesting logic of a parallel program, sometimes called "unstructured parallelism". The computational graph allows you to organize dependencies between tasks, build applications based on the transfer of messages and events.
The structure of the graph can be both static and dynamic - nodes and edges can be added and removed on the fly. You can combine individual subgraphs in a large graph.
Most of the material is based on the English publications of my overseas colleagues.
For those interested, try:
Download Intel Threading Building Blocks Library (Open Source Version):
http://threadingbuildingblocks.org
Commercial version of Intel TBB (not functionally different):
http://software.intel.com/en-us/intel-tbb
English blogs about tbb :: flow :: graph:
http://software.intel.com/en-us/tags/17218
http://software.intel.com/en-us/tags/17455
Source: https://habr.com/ru/post/157735/
All Articles