The local learning rate of neuron weights in the back-propagation error algorithm
Hi, in one of the last lectures on neural networks on the cursor, it was about how to improve the convergence of the back-propagation error algorithm in general, and in particular, consider a model where each neuron weight has its own learning speed (neuron local gain). I have long wanted to implement some sort of algorithm that would automatically adjust the speed of network learning, but all the laziness did not reach the hands, and then suddenly such a simple and straightforward way. In this short article I will talk about this model and give some examples of when this model can be useful.
Let's start with the theory, to begin with, let us remember what the change in one weight is equal to, in this case with regularization, but this does not change the essence:
In the basic case, the learning rate is a global parameter for all weights.
')
We introduce a learning rate modifier for each weight of each neuron.
, and we will change the weights of neurons according to the following rule:
In the first training batch, all learning rate modifiers are equal to one, then the dynamic tuning of modifiers in the learning process is as follows:
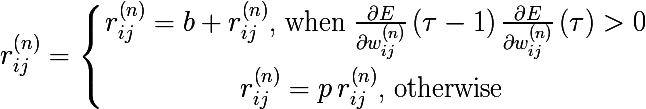
It makes sense to make a bonus a very small number less than one, and a penalty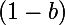
, thus b + p = 1. For example, a = 0.05, p = 0.95. This setting ensures that in case of oscillation of the direction of the gradient vector, the value of the modifier will tend back to the initial one. If you do not go into mathematics, then it can be said that the algorithm encourages those weights (growth within some dimension of the space of weights) that retain their direction relative to the previous time, and penalizes those who start to rush.
The author of this method, Geoffrey Hinton (by the way, he was one of the first to suggest using gradient descent to train a neural network) also advises considering the following things:
All experiments were carried out on a variety of pictures 29 by 29 pixels, on which English letters are drawn. One hidden layer of 100 neurons with a sigmoind activation function was used, at the output of the softmax layer , and cross-entropy was minimized. In total, it is easy to calculate that the total network is 100 * (29 * 29 + 1) + 26 * (100 + 1) = 86826 weights (including offsets). The initial weights were taken from a uniform distribution.
. In all three experiments, the same initialization of the scales was used. Also used a full batch.
A simple, easily generalizable set was used in this experiment; The learning rate (global speed) is 0.01 . Consider the dependence of the network error value on the data, on the epoch of learning.
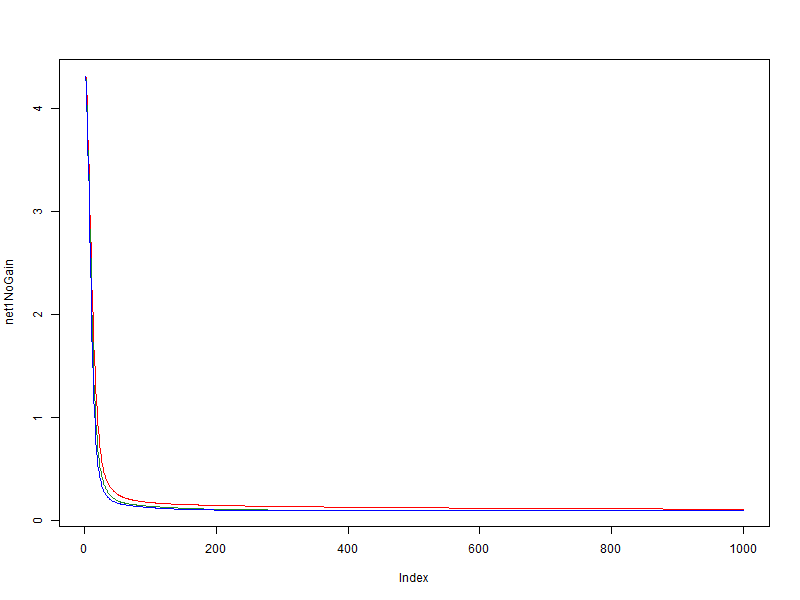
It can be seen that the modifier has a positive effect on a very simple set, but it is not great.
In contrast to the first experiment, I took a lot, which I already taught as it was. I was aware in advance that with a learning rate of 0.01 , the oscillation of the value of the error function starts very quickly, and with a smaller value, the set is generalized. But in this test 0.01 will be used, since I want to see what happens.
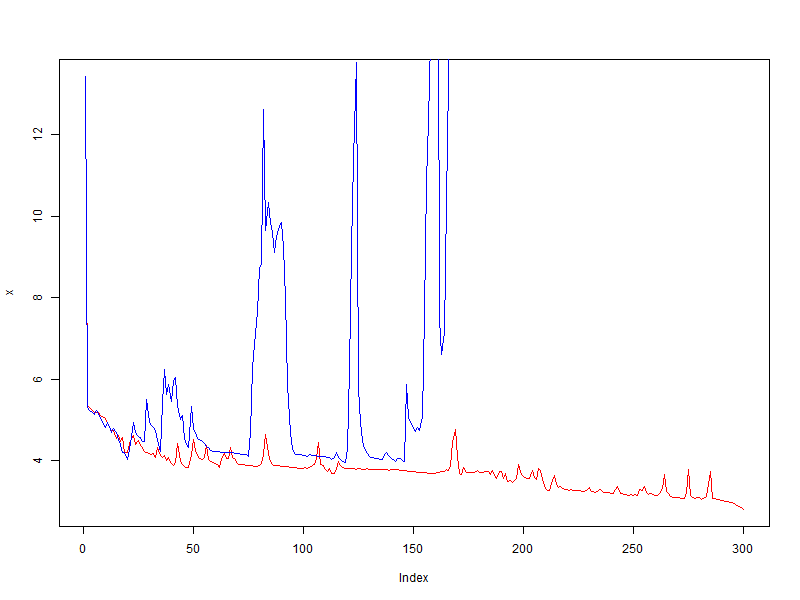
Complete failure! The modifier not only did not improve the quality, but on the contrary, it increased the oscillation, while without a modifier, the error on average decreases.
In this experiment, I use the same set as in the second, but the global learning rate is 0.001 .
In this case, we get a very significant increase in quality. And if, after 300 epochs, to drive out recognition on the training set and test:
And I made one conclusion for myself that this method is not a substitute for the choice of a global learning rate, but is a good addition to the already selected learning speed.
Theory
Let's start with the theory, to begin with, let us remember what the change in one weight is equal to, in this case with regularization, but this does not change the essence:
- this (η) is the learning rate
- m is the size of the training set
- n - layer number
- full notation here
In the basic case, the learning rate is a global parameter for all weights.
')
We introduce a learning rate modifier for each weight of each neuron.
, and we will change the weights of neurons according to the following rule:In the first training batch, all learning rate modifiers are equal to one, then the dynamic tuning of modifiers in the learning process is as follows:
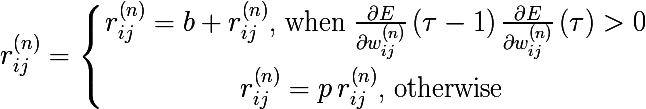
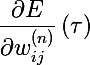- the value of the gradient at a certain point in time- tau τ - current time or current training batch
- b - an additive bonus that the modifier receives if the direction of the gradient does not change along a certain dimension
- p - multiplicative penalty, in case of changing the direction of the gradient vector
It makes sense to make a bonus a very small number less than one, and a penalty
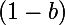, thus b + p = 1. For example, a = 0.05, p = 0.95. This setting ensures that in case of oscillation of the direction of the gradient vector, the value of the modifier will tend back to the initial one. If you do not go into mathematics, then it can be said that the algorithm encourages those weights (growth within some dimension of the space of weights) that retain their direction relative to the previous time, and penalizes those who start to rush.The author of this method, Geoffrey Hinton (by the way, he was one of the first to suggest using gradient descent to train a neural network) also advises considering the following things:
- firstly, it is worthwhile to set reasonable growth limits for modifiers
- secondly, you should not use this technique for online learning, or for small batches; it is necessary to accumulate a fairly common gradient in the batch process; otherwise, the frequency of direction oscillations increases, and thus the meaning in the modifier is lost
Experiments
All experiments were carried out on a variety of pictures 29 by 29 pixels, on which English letters are drawn. One hidden layer of 100 neurons with a sigmoind activation function was used, at the output of the softmax layer , and cross-entropy was minimized. In total, it is easy to calculate that the total network is 100 * (29 * 29 + 1) + 26 * (100 + 1) = 86826 weights (including offsets). The initial weights were taken from a uniform distribution.
. In all three experiments, the same initialization of the scales was used. Also used a full batch.The first
A simple, easily generalizable set was used in this experiment; The learning rate (global speed) is 0.01 . Consider the dependence of the network error value on the data, on the epoch of learning.
- red - without modifier
- green - bonus = 0.05, penalty = 0.95, limit = [0.1, 10]
- blue - bonus = 0.1, penalty = 0.9, limit = [0.01, 100]
It can be seen that the modifier has a positive effect on a very simple set, but it is not great.
Second
In contrast to the first experiment, I took a lot, which I already taught as it was. I was aware in advance that with a learning rate of 0.01 , the oscillation of the value of the error function starts very quickly, and with a smaller value, the set is generalized. But in this test 0.01 will be used, since I want to see what happens.
- red - without modifier
- blue - bonus = 0.05, penalty = 0.95, limit = [0.1, 10]
Complete failure! The modifier not only did not improve the quality, but on the contrary, it increased the oscillation, while without a modifier, the error on average decreases.
Third
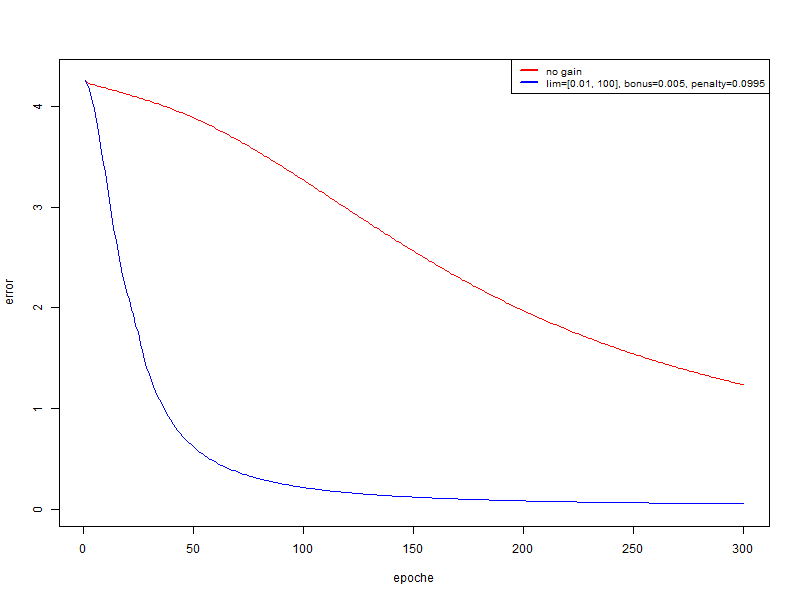
In this experiment, I use the same set as in the second, but the global learning rate is 0.001 .
- red - without modifier
- blue - bonus = 0.005, penalty = 0.995, limit = [0.01, 100]
In this case, we get a very significant increase in quality. And if, after 300 epochs, to drive out recognition on the training set and test:
- red : on the training set 94.74%, on the test set 67.18%
- blue : on the training set 100%; on the test 74.4%
Conclusion
And I made one conclusion for myself that this method is not a substitute for the choice of a global learning rate, but is a good addition to the already selected learning speed.
Source: https://habr.com/ru/post/157179/
All Articles