Parsing a task with IOI2012

Hello! In September, the International Programming Olympiad, IOI 2012, took place. And we, the Russian team, went to it very successfully, as you could see.

I am Max Akhmedov. I was offered to share with the public what are such competitions and what tasks we have to solve. I will talk about the last task of the second round of the “Jousting Tournament”. English version of the conditions can be found here . By the way, this is the simplest of the three tasks that day :-)

Legend

The task deals with the betrothal ceremony of the Duke of Lodovico Sforza, the governor of Milan, and the Duchess Beatrice d'Este, who took place in 1491. The Duke invited his good friend Leonardo da Vinci to organize celebrations and manage the cultural program of the ducal tournament.
')
And now, by the beginning of the festivities, it turned out that all the knights arrived on time, except for one who was late, but not so much as to prevent the holding of the tournament. Coincidentally, this knight was a favorite of the crowd, and all the battles with his participation were very popular. Leonardo knows the tournament schedule and how knights will be selected to participate in them, and he wants to slightly influence the course of the tournament so that the knight-favorite will take part in as many battles as possible. So the cunning PR man Leonardo is going to increase the significance of the event.

Such is the exciting story.

Formal condition

Knightly tournament is as follows. In a row there are a number of knights. Before each battle, the judge comes out and calls the knights, standing in positions that form a continuous segment, to a duel, as a result of which the winner is determined. The winner returns to his place, and the losing knights drop out. After this, the row of knights shifts, taking up empty spaces. More formally: there are N knights in a row, the judge calls the two numbers l and r, after which the knights, who are numbered from left to right, from lth to rth, fight and only the winner is left in the row. After this, subsequent battles take place on the same principle until one knight is left, who is declared the winner of the tournament.

At the moment, all N - 1 knights, except the late, have already taken their places in the row. Leonardo has the opportunity to put the arrived favorite to any place in the series, including the beginning or the end. The order of battles and the positions of the knights in them are already defined. Leonardo knows for each knight the value of his abstract “power”, expressed as an integer from 0 to N - 1. Within the framework of this task, it is considered that in a battle in which certain knights participate, in any case, the one that has the greatest value wins strength It so happened that at the tournament all knights are different in strength, that is, in any battle, the winner is determined unequivocally on the basis of their knowledge of their values. Leonardo wants to ensure that, according to the results of the tournament, the number of battles in which the crowd favorite won was as large as possible, and from all the positions leading to this outcome, he wants to choose the leftmost one. Please note: it is not necessary that our knight becomes the winner of the whole tournament! It is enough to maximize the number of battles from which he emerged victorious.

Let's look at an example. Let 5 knights participate in the tournament. Punctual knights standing in a row have the force values ​​[1, 0, 2, 4], when viewed from left to right. As you can understand, the late knight has the value of strength 3. Suppose, for example, a tournament consists of three rounds, which are characterized by the positions (2, 4), (1, 2) and (1, 2). Explain what it means.

• In the first, knights fight in the field from the second left to the fourth left.
• In the second of the remaining knights, the two who stand on the first left and second to the left will fight.
• In the last round, the remaining two knights will meet, occupying the first left and second left places.

This tournament can be more clearly displayed in the form of a tree:

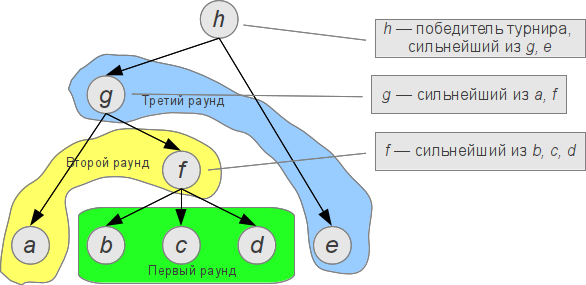
Further, by the way, we will return to such trees.

Let us understand what the tournament picture will look like, if, for example, Leonardo places a favorite to the left of all the other knights. Initially, the values ​​of the power of the knights look from left to right as [3, 1, 0, 2, 4].

• In the first round, knights will compete, having a strength of 1, 0 and 2. The knight of strength 2 will emerge as the winner, he will return to his place and the row will look like [3, 2, 4].
• In the second round our favorite will fight with power 3 and knight with power 2. The favorite of the crowd will emerge victorious, he will return, and the row will look like [3, 4].
• In the last round, our favorite will lose the knight by force 4, who will be the winner of the tournament.

Thus, our knight will win only one duel before retiring. The best solution would be to put him in a position between knights of ranks 1 and 0, forming a row [1, 3, 0, 2, 4].

• In the first round, he will take part in a battle with the knights with forces 0 and 2, from which he will emerge victorious. A number of knights now has the form [1, 3, 4].
• In the second round, he will fight with the knight of power 1, who will win.
• In the third round, he also loses to the tournament winner with a strength of 4.

As a result, the favorite wins two fights.

He cannot win more battles, as he has already won all rounds except one, and he cannot win at all, because there is a knight (having rank 4) stronger than him, who is guaranteed to be the winner of the tournament. So, the position between the first two knights is the one required by Leonardo, which is the answer to the problem.

The number of points that the program will receive depends on the effectiveness of the decision. If it works fast enough to get the correct answer in one second in situations where the number of knights does not exceed 500, then the solution will receive 17 points out of 100. If it has time to calculate the correct answer when the number of knights reaches 5000, then it will be estimated at 49 points To get the full score, the solution must manage to handle tournaments involving up to one hundred thousand knights. In our team, all four people wrote solutions that received 100 points - the task was the easiest on the tour.

Solution to the forehead

The simplest solution to the problem is to explicitly check each of the N possible positions for the late knight and find the most advantageous of them. The only technical point in the decision will be the simulation of the tournament at the given initial location of the knights. You can do this completely naively: for example, to support a number of knights in the list from left to right and in each successive round select fighting knights, find the strongest of them, put it back, and move knights to fill empty places.

This solution should pass the first group of tests in which the number of knights does not exceed five hundred. Let's estimate how much it will work, considering the order of the number of operations performed by the program. In each round, in the worst case, we need to shift almost all knights to the left, filling in empty spaces, that is, one program rounds in the worst case for the number of operations proportional to the length of the series, which on average consists of, roughly speaking, N / 2 knights. Rounds in a tournament in the worst case can be as much as N - 1, and we still need to simulate as many N possible tournaments - for all possible positions of the late knight. It turns out the dependence of N ^ 3/2 for the number of simple operations performed by the program on the number of knights N.

By the way, modern computers manage to perform about 400-500 million simple operations per second. We estimated the complexity of our solution for N = 500 as about 62 million simple operations, so we can count on the fact that it will be within the time limit with a margin. And indeed, by writing this solution, you can get a well-deserved seventeen points - this is useful if only because such a solution can be a good help for further debugging and testing the problem, the benefit is realized quite simply.

We need to go deeper

In order for the solution to work no more than a second on tests with 5,000 knights, the cubic complexity of the algorithm does not fit in any way - you need to lower the complexity estimate to at least proportional to square N. In such cases, O-big terminology is often used: we are talking about complexity O ( N ^ 2).

We need to remove one of the three factors N in the complexity estimate above. How to get rid of the external - busting positions for a late knight is not very clear. So let's increase the effectiveness of the simulation of the tournament. It would seem that we won’t leave the number of rounds - therefore, we need to make a more effective performance of one battle. We have a very inefficient piece in moving all knights to fill empty places: since the array is in the memory of an indivisible fragment and we want to quickly go to the knight in his position, this will not go anywhere. We need to somehow change the structure of their storage.

One solution would be to use instead of an array of knights of any structure that allows you to cut segments in a shorter time. But this path is very doubtful, because most of these structures do not work faster than O (log N), and the complexity of O (N ^ 2 log N) work is very dangerous: 300 million operations do not guarantee that the solution will go temporary restrictions.

The fact is that we are doing too many unnecessary operations - for some reason we support the positions of the knights in an explicit form. If you think about such a thing as a tournament tree, it becomes clear how to use it to quickly conduct all the battles. If we have to hold a round corresponding to some vertex, then it is enough for us to conduct the rounds corresponding to the child vertices, and then select the strongest from the winners of these rounds. This is done, for example, during a tour of the tournament tree in depth. Thus, if we have a tournament tree, we can conduct all the battles for linear time O (N). Outside, we still have to go over the position where we put our favorite, which also has O (N) complexity. So, we are able to perform the actual answer finding for this tree in O (N ^ 2).

It remains only to learn how to build a tree. We only need to build it once in a quadratic time, then to use it. This can be done by analogy with the way we spent rounds in a naive decision: instead of the values ​​of the knights, we would keep the vertices in the tournament tree in the row corresponding to the winning knights in these places. With each round, we will allocate a sub-segment, on which knights-tops are participating in this round, and put instead a sub-section of a new, parent for all, top.

Thus, we have a solution that requires O (N ^ 2) memory to build a tournament tree and O (N ^ 2) to find an answer on it. Such a solution with N <= 5000 should come with a margin of time and get 49 points.

We pump the solution to the full score

Let's continue to improve the solution. Tree building can be optimized by time, if instead of an array, store the vertices of the tournament tree in some data structure that can quickly cut a sub-segment (faster than O (N), as it can be done in an array). An example of such a convenient data structure is a Cartesian tree with an implicit key, which was once discussed in Habre including, and which can be read, for example, here . As a result, the implementation of the construction of the tournament tree will remain almost the same, except that the representation of the knights-tops in the row and the way of working with them will change. Thereby, the first part of the solution is optimized to O (N log N).

To optimize the second part, you need to understand that moving our one and only favorite influences the results of the tournament, in principle, not at all. For example, where the latecomer initially stands will not in any way change the winner of the entire tournament - this will in any case be the knight with the greatest force.

Let's continue to argue - is that who ever comes to a certain top of the tournament tree as a winner? It is quite obvious that this is the knight who is the strongest in the subtree corresponding to this vertex. This is a very useful consideration, it allows us to understand, for example, when our favorite can theoretically turn out to be a winner at some peak: for this it is necessary and sufficient that there is no knight stronger than him in this subtree. And what is a subtree subtree? This is a segment of a row in which punctual knights already stand - we can find the strongest knight on it, for example, using a data structure such as a segment tree .

So, for each top of the tournament tree, we can determine whether our favorite can be in it. And if he can be in it, then it is most advantageous for us to put him in such a position that the path to her in this tree is as long as possible: each vertex on the path is some kind of battle that the favorite has visited, and we are exactly the number of battles and must be maximized by the condition of the problem. So, it remains only from all the peaks available to our favorite to choose the one that contains the deepest leaf (i.e., the top of the tree that does not have “children” - this vertex corresponds to a position for the knight), and select this sheet as the answer .

Thus, the second part of the solution was also optimized to O (N log N). For N <= 100000, a solution with such complexity usually enters a time limit — this problem is no exception. Indeed, having implemented such a solution (for minor deviations), the four of us received a full score.

These are the pies

We are doing something of such an opera at our olympiads - this is a typical example of a multi-pass, serious problem from an international Olympiad with different solution paths and many logical bricks. I hope it became a little more clear what we are programming, and why we get medals then :-) See you there!