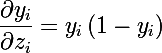Neural network with SoftMax c # layer
Hi, in the last article I talked about the error back-propagation algorithm and gave an implementation that does not depend on the error function and on the neuron activation function. Several simple examples of the substitution of these very parameters were shown: minimizing the square of the Euclidean distance and log-likelihood for the sigmoid function and the hyperbolic tangent. This post will be a logical continuation of the past, in which I will consider a slightly non-standard example, namely the Softmax activation function to minimize cross-entropy . This model is relevant for the classification problem, when it is necessary to obtain at the output of a neural network the probabilities of belonging to the input image to one of the non-intersecting classes. Obviously, the total network output for all neurons of the output layer must be equal to one (as well as for the output images of the training set). However, it is not enough just to normalize the outputs, but to make the network model a probability distribution, and train it specifically for this. By the way, now on coursera.org there is a course on neural networks , it was he who helped to delve into understanding softmax, otherwise I would continue to use third-party implementations.
I recommend to get acquainted with the previous post , since all the notation, interfaces and the learning algorithm itself are used without change here.
')
So, the first task that we face is to provide a way to model the network with a probability distribution. To do this, create a network of direct distribution, such that:
The softmax group neurons will have the following activation function (in this section I will omit the layer index, which means that it is the last and contains n neurons):
It can be seen from the formula that the output of each neuron depends on the adders of all other neurons of the softmax group, and the sum of the output values of the whole group is equal to one. The beauty of this function is that the partial derivative of the i-th neuron is equal in its adder:
We implement this function using the IFunction interface from the previous article :
In each training example, we will get a network output that models the probability distribution we need, and to compare two probability distributions, a correct measure is needed. As such a measure will be used cross entropy :
And the total network error is calculated as:

To realize the elegance of the entire model, you need to see how the gradient is calculated from one of the output dimensions or a neuron. In the previous post, in the “output layer” section, it is described that the task is reduced to the calculation of dC / dz_i, we will continue from this point on:
The last transformation is obtained due to the fact that the sum of the values of the output vector must be equal to one, according to the property of neurons of the softmax-group. This is an important requirement for the training set, otherwise the gradient will not be calculated correctly!
Let us turn to the implementation using the same representation as before:
Generally speaking, a specific layer can not be done, just in the constructor of an ordinary network of direct distribution, create the last layer, with the activation function given above, and transmit to it in the designer a link to the softmax layer, but then, when calculating the output of each neuron, the denominator of the function will be calculated each time activation, but if you implement the
then, because the network does not call the neuron's Compute method directly, but delegates this function to the layer, it can be done so that the denominator of the activation function is calculated once.
So, the missing parts are ready, and you can assemble the designer . For example, I use the same implementation of a direct distribution network, just with a different constructor .
Using
I recommend to get acquainted with the previous post , since all the notation, interfaces and the learning algorithm itself are used without change here.
')
Softmax activation function
So, the first task that we face is to provide a way to model the network with a probability distribution. To do this, create a network of direct distribution, such that:
- the network contains a number of hidden layers, all neurons can have their own activation function;
- on the last layer is the number of neurons, which corresponds to the number of classes; All these neurons will be called softmax layer or group.
The softmax group neurons will have the following activation function (in this section I will omit the layer index, which means that it is the last and contains n neurons):
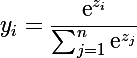 , for i-th neuron
, for i-th neuron
It can be seen from the formula that the output of each neuron depends on the adders of all other neurons of the softmax group, and the sum of the output values of the whole group is equal to one. The beauty of this function is that the partial derivative of the i-th neuron is equal in its adder:
We implement this function using the IFunction interface from the previous article :
Implement softmax function
It is worth noting that the implementation of the
double Compute(double x) method is generally not necessary, since the calculation of the output values of the group will be cheaper to do in the implementation of the softmax layer. But for completeness, and just in case, let it be -) internal class SoftMaxActivationFunction : IFunction { private ILayer _layer = null; private int _ownPosition = 0; internal SoftMaxActivationFunction(ILayer layer, int ownPosition) { _layer = layer; _ownPosition = ownPosition; } public double Compute(double x) { double numerator = Math.Exp(x); double denominator = numerator; for (int i = 0; i < _layer.Neurons.Length; i++) { if (i == _ownPosition) { continue; } denominator += Math.Exp(_layer.Neurons[i].LastNET); } return numerator/denominator; } public double ComputeFirstDerivative(double x) { double y = Compute(x); return y*(1 - y); } public double ComputeSecondDerivative(double x) { throw new NotImplementedException(); } } Error function
In each training example, we will get a network output that models the probability distribution we need, and to compare two probability distributions, a correct measure is needed. As such a measure will be used cross entropy :

- t - required outputs for the current training example
- y - real neural network outputs
And the total network error is calculated as:

To realize the elegance of the entire model, you need to see how the gradient is calculated from one of the output dimensions or a neuron. In the previous post, in the “output layer” section, it is described that the task is reduced to the calculation of dC / dz_i, we will continue from this point on:
 because the output of each neuron contains the adder of the current, we have to differentiate the entire amount. Due to the fact that the cost function depends only on the outputs of the neurons, and the outputs only on adders, it can be decomposed into two partial derivatives. Next, we consider individually each member of the sum (the main thing is to pay attention to the indices, in our case j runs through the neurons of the softmax group, and i is the current neuron)
because the output of each neuron contains the adder of the current, we have to differentiate the entire amount. Due to the fact that the cost function depends only on the outputs of the neurons, and the outputs only on adders, it can be decomposed into two partial derivatives. Next, we consider individually each member of the sum (the main thing is to pay attention to the indices, in our case j runs through the neurons of the softmax group, and i is the current neuron)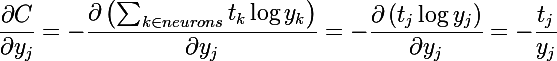



The last transformation is obtained due to the fact that the sum of the values of the output vector must be equal to one, according to the property of neurons of the softmax-group. This is an important requirement for the training set, otherwise the gradient will not be calculated correctly!
Let us turn to the implementation using the same representation as before:
Implementation of cross entropy
internal class CrossEntropy : IMetrics<double> { internal CrossEntropy() { } /// <summary> /// \sum_i v1_i * ln(v2_i) /// </summary> public override double Calculate(double[] v1, double[] v2) { double d = 0; for (int i = 0; i < v1.Length; i++) { d += v1[i]*Math.Log(v2[i]); } return -d; } public override double CalculatePartialDerivaitveByV2Index(double[] v1, double[] v2, int v2Index) { return v2[v2Index] - v1[v2Index]; } } Softmax layer
Generally speaking, a specific layer can not be done, just in the constructor of an ordinary network of direct distribution, create the last layer, with the activation function given above, and transmit to it in the designer a link to the softmax layer, but then, when calculating the output of each neuron, the denominator of the function will be calculated each time activation, but if you implement the
double[] ComputeOutput(double[] inputVector) neural network properly: public double[] ComputeOutput(double[] inputVector) { double[] outputVector = inputVector; for (int i = 0; i < _layers.Length; i++) { outputVector = _layers[i].Compute(outputVector); } return outputVector; } then, because the network does not call the neuron's Compute method directly, but delegates this function to the layer, it can be done so that the denominator of the activation function is calculated once.
Softmax layer
internal class SoftmaxFullConnectedLayer : FullConnectedLayer { internal SoftmaxFullConnectedLayer(int inputDimension, int size) { _neurons = new INeuron[size]; for (int i = 0; i < size; i++) { IFunction smFunction = new SoftMaxActivationFunction(this, i); _neurons[i] = new InLayerFullConnectedNeuron(inputDimension, smFunction); } } public override double[] Compute(double[] inputVector) { double[] numerators = new double[_neurons.Length]; double denominator = 0; for (int i = 0; i < _neurons.Length; i++) { numerators[i] = Math.Exp(_neurons[i].NET(inputVector)); denominator += numerators[i]; } double[] output = new double[_neurons.Length]; for (int i = 0; i < _neurons.Length; i++) { output[i] = numerators[i]/denominator; _neurons[i].LastState = output[i]; } return output; } } Total
So, the missing parts are ready, and you can assemble the designer . For example, I use the same implementation of a direct distribution network, just with a different constructor .
Constructor Example
/// <summary> /// Creates network with softmax layer at the outlut, and hidden layes with theirs own activation functions /// </summary> internal FcMlFfNetwork(int inputDimension, int outputDimension, int[] hiddenLayerStructure, IFunction[] hiddenLayerFunctions, IWeightInitializer wi, ILearningStrategy<IMultilayerNeuralNetwork> trainingAlgorithm) { _learningStrategy = trainingAlgorithm; _layers = new ILayer[hiddenLayerFunctions.Length + 1]; _layers[0] = new FullConnectedLayer(inputDimension, hiddenLayerStructure[0], hiddenLayerFunctions[0]); for (int i = 1; i < hiddenLayerStructure.Length; i++) { _layers[i] = new FullConnectedLayer(_layers[i - 1].Neurons.Length, hiddenLayerStructure[i], hiddenLayerFunctions[i]); } //create softmax layer _layers[hiddenLayerStructure.Length] = new SoftmaxFullConnectedLayer(hiddenLayerStructure[hiddenLayerStructure.Length - 1], outputDimension); for (int i = 0; i < _layers.Length; i++) { for (int j = 0; j < _layers[i].Neurons.Length; j++) { _layers[i].Neurons[j].Bias = wi.GetWeight(); for (int k = 0; k < _layers[i].Neurons[j].Weights.Length; k++) { _layers[i].Neurons[j].Weights[k] = wi.GetWeight(); } } } } Source: https://habr.com/ru/post/155235/
All Articles