Rotating beatboards: a new round of old ideas

Short description
This article talks about some of the nuances in the use of "bitboards" (a 64-bit integer, each bit of which represents one chessboard field). Back in 1994, after the ACM Chess Symposium held at Cape May in New Jersey, I decided to completely replace the program for Cray Blitz (computer program written by Robert Hiat, Harry Nelson and Albert Gov for the Cray supercomputer - approx. transfer.). I was interested in trying the bitboards method tested by Slate and Atkin in “Chess 4.x” (chess program developed at Northwestern University of Illinois, and dominant in the 70s of the 20th century - note of the translation.) To decide for yourself whether it is suitable for chess or not. During the development of this new program, the concept of “spinning bitboards” was invented, and it turned out that this was the very thing needed to make this type of data structure work with acceptable performance.
1. Introduction
Bitboards are mentioned many times in computer chess literature. In the mid-1970s, Slate and Atkin invented and described a method of using twelve 64-bit integers, each of which represented one type of chess pieces on the board (six for white and six for black). It should be noted here that the KAISSA team (Donskoy and others), apparently, invented the same idea independently of the team of Northwestern University, and that in the last 25 years many other programs have been written using the same approach.
')
Slate suggested matching bits to the fields of a chessboard; a bit with a value of 1 served as a sign of the presence of a piece on a chessboard, while bit 0 indicated its absence. Thus, in a whiteboard, white_pawn, which corresponds to the fields occupied by white pawns, can be at most eight bits with a value of 1. (In this article, the fields are numbered from 0 to 63, where the position 0 corresponds to the field A1, 7 corresponds to the field H1, 56 matches the A8 field, and 63 matches the H8 field. The bits that are at position 0 in the 64-bit integer are called the “most significant bits,” and the bit at position 63 is called the “least significant bit.”) (most significant bit, MSB) and least significant bit, LSB - approx. translation.)
In addition to storing position information on the board in these twelve 64-bit words, Slate and Atkin described how to generate and consistently update two additional sets of bitboards for information of a different kind. attacks_from [64] - an array of bitboards with values of 1 for each field that can be attacked by a figure standing on a given field. For example, attacks_from [E4] gives us fields that are directly attacked by a figure standing on the E4 field. In addition, the array of attacks_to [64] contains bitboards with bits 1 for all fields occupied by figures attacking a given field. For example, attacks_to [E4] is a beatboard that contains bits 1 for all the fields on the board, where there is an E4 beating field.
These two sets of bitboards are the subject of this article, which describes a new and very fast way to dynamically calculate bitboard attacks_from [] without significantly reducing the speed of execution, which was the case for the update method described by Slate and Atkin. (It should be noted that Slate / Atkin used a sequential update because the procedure described below is too slow to calculate the attacks of long-range pieces on the fly. In order to somehow get the beatboards to work and avoid high computational costs, they resorted to a sequential update .)
There are other useful properties of bitboards that make them very useful in chess programs. One of these properties is something that could be called "bit-parallel" operations. For example, in traditional chess programs, if you have a pawn on E4, and you want to check whether it is a pass, you will have to check the D5, E5, F5, D6, E6, F6, D7, E7, F7 fields to make sure that there is no enemy pawns. This requires nine comparisons. Using beatboards, you just need to pre-calculate the array of masks for each field where a pawn can stand, and then take the is_passed_white [E4] mask and perform a bitwise “AND” (AND) operation with the beatboard for black pawns. If you have correctly computed the mask so that it has units in each of the nine top fields, one AND operation can determine the absence of black pawns or, on the contrary, their presence, which will not allow the white pawn on E4 to be passed. In fact, we performed 9 different checks in parallel and in just one AND operation answered nine questions at the same time.
There are other advantages, but the topic of this article is rotating bitboards and how they can be used as needed to obtain data from the arrays of attacks_from [64] and attacks_to [64], without restrictions imposed by sequential updates, and without complex / slow cycles .
2. Calculation of the array of attacks_from [64] using normal bitboards
Before proceeding to the method of rotating bitboards, you need to pay attention to the complexity of computing attacks_from []. For short-lived figures, this is of course very simple; we can, for example, prepare in advance an array of knight_attacks [64] so that if the knight stands on the F6 field, then knight_attacks [F6] is a bitboard containing bit 1 in all the fields where the knight from the F6 field can attack (note that , attacked by a knight, do not depend on the placement of pieces on a chessboard). The same idea works for the king and for the pawns (with a few changes, since the pawns hit diagonally, and without taking they move forward one or two fields).
However, for long-range figures, simple access to the array (as was done above) does not work, because long-range figures attack only in the direction of their movement and only the first figure that they encounter in this direction. So, how do we calculate this?
First, we will need a bitboard named occupied_squares, which is nothing more than a bitboard with units placed in all fields where any piece of any color stands (for example, it can be viewed as the result of bitwise OR (OR) between all twelve bitboards for each type of pieces, although in fact we store two such bitboards: one for black and one for white - and use the OR operation between them if necessary to get the occupied_squares bitboard).
Figure 1 shows an example of a chess position where the occupied fields are marked with an “X” and the unoccupied fields are marked “-”.

Notice that it doesn’t matter what exactly is in the fields, because the long-range figure stops when it encounters a figure of any kind. If the bishop is on the F5 field (for clarity, it is marked with the B symbol in Figure 2), then we see that it directly attacks the following set of fields: {B1, C2, D3, E4, G6, H3, G4, E6, D7}. After we calculate the bitboard of the attacks (if this is what the admissible moves of the bishop will be used for from this position), we may need to exclude all the moves that are beaten by our own pieces. Using the white_occupied bitboard mentioned earlier, we can apply an add operation (bitwise negation) and then an AND operation with a bitboard of attacks, which will drop those bits that match the attacks on our own pieces in the bitboard of an elephant's attacks, since these are unacceptable moves.
So far so good. But how do we define the attacked bits without enumerating all 4 (or 8 for the queen) rays along which the piece can move? This, in general, is not so difficult, but not very effective in that each direction requires a separate iteration of the cycle.
First, we will create a set of masks for each of the 8 directions in which the figure can move. Let's call them plus1 [64], plus7 [64], plus8 [64], plus9 [64], minus1 [64], minus7 [64], minus8 [64], minus9 [64]. These bitboards contain bit 1 for any field that can attack an bishop from the SQ field in a given direction. For our example with an elephant on F5 in the direction of plus7 (these are fields F5-E6-D7-C8) plus7 [F5] it will look like that shown in Figure 3.
This will give us all the fields that an elephant can attack in the direction of +7, if there were no blocking figures between the elephant and the edge of the board. But we know that they may be present, and, if so, we must find the blocking figures in this direction. In order to do this, we take the above bitboard and make AND between it and occupied_squares bitboard. If the bishop is blocked in this direction, we will get a non-empty bitboard, in which bits 1 will stand for each field, where there is a figure blocking the bishop's movement diagonally to C8. Since we only need the first blocking figure, we will use the FirstOne () function, which will return the index of the first bit with value 1. For example, if the elephant was blocked on C8 and D7, FirstOne () should return the field number D7 (51).
Now we have a list of attacked fields along this diagonal and a field where the long-range figure is blocked. All that is left for us to do is to remove the attacked fields after the blocking figure. And this is just the easiest part. The following code example explains how to do this:
diag_attacks = plus7 [F5]; blockers = diag_attacks & occupied_squares; blocking_square = FirstOne (blockers); diag_attacks ^ = plus7 [blocking_square];
That's all you need to do for one ray. To make the code clearer, diag_attacks is the bitboard described above, which contains the attacked fields from the F5 field in the +7 direction. Blockers is a beatboard with all the pieces on a given diagonal. We find the first blocking figure and then make an exclusive “OR” between plus7 [blocking_square] and diag_attacks, which actually “cuts off” all the attacked fields that follow it. (Let's try to figure it out. If the bishop from F5 is blocked on E6, then plus7 [E6] in this case will look like this: the bits with units will be only on D7 and C8. Since the D7 / C8 bits are nonzero in both bitboards, then after the exclusion " OR "between bitboards, these (and only these) bits are reset.)
We repeat this for all four directions with the only difference that for negative directions we do not use FirstOne (), since we need to find the last blocking figure. Instead of this, we switch to LastOne (). Now the code for counting the attacks of the elephant in all four directions looks like this:
diag_attacks = plus7 [F5]; blockers = diag_attacks & occupied_squares; blocking_square = FirstOne (blockers); bishop_attacks = diag_attacks ^ plus7 [blocking_square]; diag_attacks = plus9 [F5]; blockers = diag_attacks & occupied_squares; blocking_square = FirstOne (blockers); bishop_attacks | = diag_attacks ^ plus9 [blocking_square]; diag_attacks = minus7 [F5]; blockers = diag_attacks & occupied_squares; blocking_square = LastOne (blockers); bishop_attacks | = diag_attacks ^ minus7 [blocking_square]; diag_attacks = minus9 [F5]; blockers = diag_attacks & occupied_squares; blocking_square = LastOne (blockers); bishop_attacks | = diag_attacks ^ minus9 [blocking_square];
This translates into a large number of operations with AND and OR and the need for masking, plus the use of the FirstOne () / LastOne () functions to detect a blocking field. This is very expensive, but since most of the work is done in parallel with boolean operators, it can still be worth it. However, there is a better way that allows you to get rid of the FirstOne () / LastOne () calls and that processes the entire diagonal / horizontal / vertical in one step, not two, as in this method.
It should also be noted that the FirstOne () / LastOne () functions are very expensive if performed as procedures in C, because finding the first or last bit is a non-trivial task that takes a lot of time with the above calculation of attacks. Fortunately, modern microprocessors have hardware instructions for calculating these values (Intel has BSF / BSR instructions [bit-scan forward, bit-scan reverse] in the X86 architecture), which makes these functions extremely fast. Other types of architecture also offer similar instructions.
3. Rotating beatboards
After the hit-board version of Crafty appeared in September 1994, I started conducting seminars at UAB (Crafty is a chess program written by Robert Hayat, UAB - University of Alabama at Birmingham - approx. Translation) to learn 64-bit approach and develop new ways to increase efficiency. One of the first discussions was about how easy it is to generate the movement of a long-range figure along the horizontal.
If you take any field on some horizontal (horizontal row of fields on a chessboard), then the movement of a long-range piece is easy enough to get, because the horizontal is determined by 8 bits in occupied_squares bitboard. If we move this bitboard to the right so that its lower digits turn out to be 8 bits of our horizontal, and then make AND with the number 255, then we will get 8 bits that correspond to the fields of this horizontal.
With this in mind, consider the array of bitboards rank_attacks [64] [256]. To initialize this array, take any field, for example, A1. You can see that its horizontal has only 256 different states, depending on which fields are occupied and which are not. If, before starting the game, we calculate in advance which fields the rook from A1 can go to, taking into account all 256 different combinations of single bits on this horizontal, we can receive fields attacked on this horizontal simply by referring to the bitboard rank_attacks [A1] [contents], where contents is an 8-bit representation of the state of this horizontal. All we need to do is to calculate the set of bitboards for each of the 64 fields and all 256 different states of the contour lines on which these fields are located (yes, if you think about it, the horizontal can have only 128 states, because we _ know_ that one of the fields is the rook, but it is easier to ignore this simplification). It should be noted here that, although the horizontal has 8 state bits, the two extreme bits (LSB and MSB) do not change anything, since they are attacked regardless of whether they have a figure or not. As a result, we remove them from further calculations in order to reduce the size of the table for each horizontal by 75%. Thus, we reduce the size of the array rank_attacks to rank_attacks [64] [64]. All other similar arrays will use the same simplification.
So far so good, we can get half of the rook attacks by simply accessing the memory with the rank_attacks array. But what about attacks on the vertical and two diagonals for elephants? There, the bits are not adjacent to occupied_squares in the bitboard, and this makes our idea inapplicable for anything other than the horizontal lines.
During the discussion of this at the seminar, we noticed that when using specialized chess equipment, we would probably allocate a register to store the 64-bit value of occupied_squares, but then we could identify three other “pseudo-registrars” that would allow us to turn to occupied_squares different ways. For example, one will rotate the entire contents of occupied_squares by 90 degrees so that now the bits on one vertical become adjacent; and we will be able to use this to find attacks on the vertical just as we did with the pre-calculated attacks on the horizontals. And we can select two registers that will rotate the occupied_squares bitboard left and right by 45 degrees so that the diagonal bits in these rotating bitboards will become adjacent. Figure 4 illustrates how the fields are numbered in a regular beatboard for a chessboard.

Recall that A1 is the zero bits (MSB), and H8 is the 63rd bit (LSB) in occupied_squares bitboard. First of all, we rotate it to the left by 90 degrees to make the vertical bits adjacent (note that the lower left corner remains zero in the 64-bit bitboard, and the upper right corner will always have a serial number 63), as shown in Figure 5.
Then we rotate the original 45 degrees to the left, as shown in Figure 6.

In this bitboard turned, the bottom field (A1) becomes zero in a bit, and the next ones become in order. So, for example, A2 becomes bit 1, B1 becomes bit 2, and so on to H8, which becomes bit 63.
Note that in the above bitboard, the bits on the diagonal from H1 to A8 and on all the diagonals that are parallel to it are now adjacent. This is not as convenient as in the first two bitboards; there we could easily calculate how much the given horizontal or vertical should be moved to the right end of the number so that it can be used as an array index; and we also knew that in order to extract the eight necessary bits, we need to make AND with the number 255. In the case of diagonals, we have a different length for each diagonal, which means a different shift value and a mask to eliminate the extra bits. The solution to this problem will be described later.
Now we rotate the original bitboard 45 degrees to the right to make adjacent bits on the other diagonals, as in the bitboard in Figure 7.
Now that we have it all, it becomes obvious that we need to add three more arrays of bitboards for attacks in addition to the already considered rank_attacks [64] [64]. File_attacks [64] [64], diaga1h8_attacks [64] [64] and diagh1a8_attacks [64] [64] are added, and if we learn to rotate the occupied_squares bitboard, we will be able to use the same indexing scheme update procedure for two calls to the table for elephants or rooks and four for queens.
Later, after long discussions about the occupied_squares rotation of bitboard, a simple solution was found. Instead of storing the only bitboard occupied_squares and rotating it if necessary (which we think is almost impossible due to inefficiency), we can store four faceboards for the occupied fields: plain and rotated 90 degrees, 45 degrees left and 45 degrees right. It's really quite easy, because in the procedure of moving the MakeMove () figure we can find a similar code for updating the occupied_squares bitboard:
occupied_squares ^ = set_mask [from] | set_mask [to];
This is a simple mechanism for normal moves (taking, castling and taking on the aisle are processed a little differently), because we know that the bit of the starting “from” field in occupied_squares must be set to 1 (otherwise there would not be a figure in this field). ); and we also know that the bit of the final “to” field in a occupied_squares bitboard must have a zero value (otherwise it would be a capture). So, using the exclusive "OR" bit of the start field is cleared, and the bit of the final field is set.
All elements of the set_mask [64] bitboard array have only 1 set bit in the corresponding position. For example, the leftmost bit (zero bit) is set to set_mask [0], while the least significant bit (63rd bit) is set to set_mask [63]. To work with rotating bitboards, we created three new sets of such masks: set_mask_rl90 [64], set_mask_rr45 [64] and set_mask_rl45 [64]. Each of them accepts the field number as an index, and returns the bitboard in which the occupied_squares bit in the rotating bitboard is set. For example, in set_mask_rl90 [0] the seventh bit is actually set, since if you look at the picture, bit 0 in the rotated_left bitboard becomes the seventh.
This was the solution we needed to make everything work. Instead of rotating the occupied_squares bitboard, we now store four occupied_squares bitboards at a time and can use two of them for bishops / rooks or four for queens at any time when we need to get attacks for these types of pieces.
For elephants, there is one good optimization that can be used, although it is expensive relative to memory. Recall that for the rooks we moved the corresponding horizontal or vertical to the right end of the number, then we did AND from 255 to get the contents of this horizontal or vertical. It worked, since each horizontal or vertical contains eight bits. But in the case of diagonals, each differs in length from its neighbor.
To simplify this algorithm, we will do AND 255 in the case of diagonals, which, obviously, will give us the desired diagonal, but with a few extra bits from the next diagonal (diagonals). If the diagonal we are interested in has only three bits (a total of 8 unique states), we get each of these 8 states combined with 32 states of extra bits. In other words, we have the states of the three bits we need, which are repeated 32 times. Thus, it does not matter what is contained in the extra 5 bits, we still get the correct beatboard attack for our three-bit diagonal.
4. Calculation of attacks_from [64] using rotated bitboards
To calculate the attacks, we use 4 different arrays: one for attacks horizontally, one for attacks vertically, and one each for the two diagonals that pass through the field. We called these arrays rank_attacks [64] [64], file_attacks [64] [64], diaga1h8_attacks [64] [64] and diagh1a8_attacks [64] [64].
To initialize these arrays (this is done when the application is started, and from this point on, the arrays remain unchanged) we simply assumed that the field has a long-range piece that can move in the direction in question (for example, the queen). Then for each field we entered rank_attacks [square] [rank_contents] - a bitboard, which shows which horizontal fields the rook / queen standing on the “square” field can move in when the horizontal fields are occupied by eight bits of the number “rank_contents” ". For example, let's take the occupied_squares considered earlier, but instead of the bishop on the F5 field, as in the previous example, we will put the rook there (Figure 8). Suppose we are trying to initialize rank_attacks [37] [100] (37 is the F5 field, and 100 corresponds to the occupied fields on this horizontal line - 01100100). We initialize this element rank_attacks, as shown in Figure 9. This fully corresponds to the fields that the rook / queen can attack on the 5th rank, if the piece is on F5, and the horizontal is occupied by three pieces, as mentioned above.
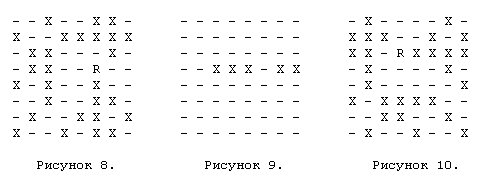
Well, not bad. By doing this, we can quickly get rook attacks along the horizontal. But now we need to calculate the attacks not horizontally, but along the vertical. To do this, we take the occupied_rl90 bitboard, which is an exact copy of the previous occupied_squares, but rotated 90 degrees, as shown in Figure 10.
When we extract the third "horizontal", we actually get information about the employment on the vertical F (perhaps, the third above horizontal is meant - approx. Translation.). Again, pre-calculated bitboards of attacks are used again, but this time we take attacks_file [37] [251] (again, 37 means F5 field, and occupied fields on this vertical form 11111011), the value of which we determined as shown in the figure eleven.
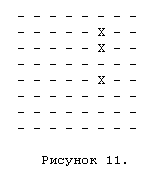
Now, taking both of these values — attacks along the horizontal and attacks along the vertical — and making OR between them, we get a full set of attacked fields for the rook on F5, for a special case with given positions horizontally and vertically.In the case of the queen, we also use two bitboards for diagonal attacks and two occupied_squares rotated diagonally to get diagonal attacks in the same way, and at the end do the OR between diagonal and vertical / horizontal attacks. Notice that there are no cycles here. The algorithm for the long-range figure is as follows:
BITBOARD attacks = 0;
if (BishopMover (piece)) {
get diaga1 status (shift / AND); / * 6 bits *
attacks | = diaga1h8_attacks [square] [status];
get diagh1 status (shift / AND); / * 6 bits *
attacks | = diagh1a8_attacks [square] [status];
}
if (RookMover (piece)) {
get rank status (shift / AND); / * 6 bits *
attacks | = rank_attacks [square] [status];
get file status (shift / AND); / * 6 bits *
attacks | = file_attacks [square] [status];
} And that's it, we're done, completely. The two conditions BishopMover () and RookMover () return TRUE if the piece walks diagonally, like an elephant (elephant or queen), or moves like a rook (rook or queen). In Crafty, this is encoded in a shape type, where P = 1, N = 2, K = 3, B = 5, R = 6 and Q = 7. When analyzing these numbers, the result of piece_type & 4 is checked, and if the result is non-zero, this is a long-range figure. Further, if the result of piece_type & 1 is non-zero, this figure walks diagonally, and if the result of piece_type & 2 is nonzero, then the figure can move along the horizontals / verticals.
5. Calculation of attacks_to [64]
The attacks_to [] bitboard was defined by Slate and Atkin as a one-bit beatboard for each field from which an attack is made on this field. For example, attacks_to [28] (28 = E4) might look like the one shown in Figure 12, if we assume that E4 is attacked by the black rook on E8 and the black knight on F6, and is protected by the white rook on E1 and the white pawn on D3 (E4 marked with the letter T, from "target").
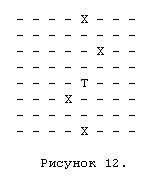
In this picture, “T” is the attacked field, in fact, it corresponds to bit 0 in the bitboard. The four bits X (bits 1) show the four fields from which the figures standing on them make attacks on the field E4. If we want to know how many black pieces are attacking E4, we can simply make AND of this bitboard occupied_squares with blackboards for black pieces. The result will have bits 1 on each field occupied by a black piece that attacks E4. Similarly, with attacking E4 white pieces, we also do occupied_squares AND with a bitboard for white pieces.
The questions are as follows: (a) How can we calculate such a bitboard and (b) how difficult is it? Using the above method of generating attacks for bitboards (remember that generating attacks for short-range figures is trivial, since all fields attacked by a figure, unlike long-range figures, can be calculated at the start of the application and will not change in the future) , and then we will do AND with a bitboard for white / black bishops and queens, which will give us 1 bit for each bishop / queen, regardless of their color, which attack the target field. We remember the result and do the same for the rooks and the beatboards of the rooks / queens. Then we take the knight's bitboard attacks, do AND with the bitboard for white / black horses and repeat it for kings and pawns. As a result, we have five bitboards, which, if you make an OR between them, will show all the fields,from which an attack is made on E4.
Now, when we can get a set of fields that a piece can attack (used when generating a turn) and a set of fields from which an attack is made on a certain field (used, for example, to determine whether the king is under check). information in the chess program.
6. Using beatboards in a chess engine
It is important to note that the indicated algorithm gives a bitboard with a complete set of moves of a certain figure, without using any cycles. However, in a chess program, these movements have to be broken down into a set of individual “from / to” moves for their evaluation, and this process will definitely be a cycle, albeit a very simple one. The from where field is known, so we simply use the FirstOne () function to turn the first bit into an integer corresponding to the where field, and then reset this bit. The cycle continues until all bits are cleared. Below is the real code that does exactly that for the white queen: (note that in Crafty, the move is stored in 21 bits. The low 6 bits indicate the FROM field (from where), the next 6 - the TO field (where), more 3 is MOVING_PIECE (the figure to be moved), and the last 3 is the PROMOTE_TO figure,which pawns turn into.)
piecebd=WhiteQueens;
while (piecebd) {
from=LastOne(piecebd);
moves=AttacksQueen(from);
temp=from+(queen<<12);
while (moves) {
to=LastOne(moves);
move_list[i++]=temp+to<<6;
Clear(to,moves);
}
Clear(from,piecebd);
} At first glance, this may seem rather ineffective, but when studying a chess program and the task of evaluating a move, it turns out that the moves that need to be evaluated are primarily taking. In order to generate only moves with captures, you just need to get the above-mentioned bitboard attacks and then make AND with a bitboard containing all the fields occupied by the opponent’s pieces — after that, only those bits that match the captures remain. Consequently, in the generation of takes, which are the largest part of the chess tree, only a few move in the cycle leading to the capture of an enemy piece, moves; there is no search of empty fields between the long-range figure and the figure it beats, and there are no special checks on whether we reached the edge of the board or not. As a result, it turns out to be a significant gain in comparison with the traditional approach.Below is the same code for the white queen, but for taking exclusively.
piecebd = WhiteQueens;
while (piecebd) {
from = LastOne (piecebd);
moves = AttacksQueen (from) & BlackPieces;
temp = from + (queen << 12);
while (moves) {
to = LastOne (moves);
move_list [i ++] = temp + to << 6;
Clear (to, moves);
}
Clear (from, piecebd);
} It is simple and straightforward, and if the queen does not have a single move with the capture of an enemy figure, the inner loop will never be executed at all. If you want, you can pass your goalsboard to your beatboard move generator. To generate all the moves, pass the target bitboard, which is a simple addition of occupied_squares to the implementing side, and as a result all the moves will be generated (except for taking your own pieces).
As previously shown, it is quite simple to get the attacks_to [] bitboards if necessary. It does not have high computational complexity, is easily implemented and provides functionality (attacks_to [sq]), if / when it is needed. The most frequent use for this type of information is the answer to the question “Is the king under the check?”, Which is even easier to do than described earlier. For each type of pieces (bishop / queen, rook / queen, knight, king, and pawn) we generate a beatboard of attacks and then do AND for each of them with a bitboard of an enemy piece (we don’t care if our pieces attack our own king, only opponent's pieces), and if the result is non-zero, we immediately return “TRUE”, saying “yes, the king is attacked and under the check”.
This can also be used to implement a static block for calculating exchanges used in evaluating moves. For some field where we need to calculate the sequence of exchanges, we first take attacks_to [sq], which gives each figure that directly attacks this field. Find the least significant enemy figure that attacks this field; for this, we do AND between attacks_to and each of the six bitboards for enemy pieces, starting with the pawns and moving up to the king ascending the value of the piece. When the result of AND is a non-zero result, we will know the value of the figure that will have to attack the target field first. We discard this attacking figure from attacks_to, since it has already been used, after which we make AND the resulting attacks_to with six bitboards for our figures,to get the defender with the lowest cost. Repeat until the attacks_to becomes empty.
However, what about long-range figures that attack the target field so that one is behind the other? It is also easy to calculate. We know the figure that we just “used” by dropping it from the attacks_to bitboard, so that we can determine whether it is long-range or not (for example, a pawn, bishop, rook, or queen, behind which there are other pieces, can form a “battery” ). We just need to do another AND operation to find out if there is another figure in this direction behind the one we just used. If this is so, and it is of a suitable type (bishop / queen for diagonals, rook / queen for horizontals / verticals), we simply do OR of this figure with attacks_to, as a result of which it now attacks the target field, without having any interference in front of it. (we use the now familiar bitboards plusN [] / minusN [],and leave the answer to the question how to do this as an exercise for the reader.)
Pay attention, we considered only the question, whether the figure is attacking the field or not, nothing more. This can be applied to a king, to a more significant figure, or to overload to protect two fields at the same time. Errors are therefore possible. However, for one field, the algorithm works quite accurately. For example, in the case when we have three pieces in the battery (say, a queen and two rooks), the queen standing in front can become a problem, since in analyzing the exchange we must be sure that he will be the first to be used. This algorithm guarantees this, since the rooks will not be reflected in attacks_to until the queen is removed.
7. Conclusion
There are many advantages of using bitboards, but today the most important is “data density”. Note that all 64 bits are important, even if many end in zeros, since they reflect the status of some field. This means that since the CPU moves these 64-bit bitboards, it does not waste internal bandwidth on moving unused data, which happens when a regular chess program runs on a 64-bit machine. There, most 64-bit words are not used, they are simply additional, unnecessary information.
For current 64-bit architectures (Alpha, HP, MIPS are just a few of them) and for new 64-bit architectures, such as the Intel Merced processor, using bitboards makes tremendous sense, because here beatboards take maximum advantage of the size of the internal register of the processor and tires. For example, most of the usual bit operations (AND, OR, XOR, shift, and so on) on 32-bit machines use at least two instructions — one for each half of the 64-bit bitboard. On the 64-bit architecture with the same clock frequency, these operations are performed twice as fast, because they only require one instruction to be processed. This is a performance gain that should not be neglected, because it is absolutely free.
Many programs now use bitboards for some functions, such as calculating the pawn structure (because it is a convenient and compact way of representing pawns as one variable), determining whether the king is under check or not (since just a single AND operation allows bitboards to be very simple decide if a piece can attack the king), and for other purposes. Chess 4.0 began the revolution of bitboards, being the first program to use them exclusively for the presentation of the board, and programs like Crafty (there are many others. Too many to list), continued this development. However, it is likely that the main improvements in performance when using bitboards came from the Crafty project, when, as an alternative to the regular sequential update, which found a place in “Chess 4.0”,the concept of “rotated bitboards” was invented, which gave a significant increase in performance without losing opportunities. Currently, the most burning question is “how else can you use beatboards in a chess program to further increase its performance?”. There is a big danger of abuse of bitboards. As the old adage warns, “for a man with a hammer, everything looks like a nail” (“make the fool pray to God, he will break his forehead” - approx. Translation.) However, it is very important that we (at least once) try to pound everything around to see if the hammer will work, or better find another tool for some tasks.Currently, the most burning question is “how else can you use beatboards in a chess program to further increase its performance?”. There is a big danger of abuse of bitboards. As the old adage warns, “for a man with a hammer, everything looks like a nail” (“make the fool pray to God, he will break his forehead” - approx. Translation.) However, it is very important that we (at least once) try to pound everything around to see if the hammer will work, or better find another tool for some tasks.Currently, the most burning question is “how else can you use beatboards in a chess program to further increase its performance?”. There is a big danger of abuse of bitboards. As the old adage warns, “for a man with a hammer, everything looks like a nail” (“make the fool pray to God, he will break his forehead” - approx. Translation.) However, it is very important that we (at least once) try to pound everything around to see if the hammer will work, or better find another tool for some tasks.) However, it is very important that we (at least once) try to knock everything around to see if the hammer will work, or it is better to find another tool for some tasks.) However, it is very important that we (at least once) try to knock everything around to see if the hammer will work, or it is better to find another tool for some tasks.
Author: Robert Hayat
Original: http://www.cis.uab.edu/info/faculty/hyatt/bitmaps.html
From translator
This article assumes that the reader has some initial knowledge of beatboards and how a chessboard is represented with the help of them. However, there is a lot of information about this, there are many good translations into Russian, so it’s easy to get acquainted. I translated this article, because, unfortunately, I did not find a single good translation of exactly the methods of rotating and magic beatboards.
As a reference, I recommend to look at the following links:
www.frayn.net/beowulf/theory.html#bitboards
www.craftychess.com
I took the liberty to translate the English word “bitboard” as “bitboard”, since I have found a common chess term failed, and the Russian “bit field”, which is close in meaning, is ambiguous and cumbersome.
In English, the words “bitmap” and “bitboard” are synonymous, while the Russian concepts “bit field” and “bitmap” differ significantly in meaning. In both cases, I use the word "bitboard".
In programming, bitwise operations sound more familiar in English, so I left the English versions: AND, OR, etc., but for clarity, I also gave the Russian version when the first occurrence of such a word.
Source: https://habr.com/ru/post/155045/
All Articles