Game "Life". Again. This time in 3D
For the last week Habr has replenished at once with several articles about the game "Life". Well, then I will share my insights on this topic.
Last summer I had the opportunity to visit the summer school on parallel programming, conducted by the NSU. Within the school, each student had to prepare a project on one of the topics voiced at the lectures. I was interested in cellular automata. My first association with the phrase “cellular automaton” is “Life”.
I realized that no one would be interested to watch the black cells living on the screen. And it’s too easy for such a project. It was necessary to come up with something fundamentally new. I decided to expand the range of my thoughts and go beyond the limits of two-dimensional space. Literally. I thought, why not make this game three-dimensional? It's so much more interesting!
I think that here everyone (or almost everyone) imagines a cellular automaton. Therefore, we will not delve into the theory, but immediately proceed to practice. The only thing that distinguishes this cellular automaton from the most primitive is that it was necessary to parallelize the calculations. In the future, however, something else will be added, but for now let's not talk about it. The cellular automaton (hereinafter the KA) for our purposes should be synchronous. Fortunately, even with a parallel implementation of the algorithm, this does not create any inconvenience. When working with OpenMP, it is enough to simply place a loop that calculates the value of the spacecraft in the #pragma omp for {} block.
')
It would not be bad if all this could be seen firsthand. And I was lucky, because literally a month before that I had little experience in working with OpenGL using the freeglut library. I also wanted the game space to be able to rotate, zoom in and out. Management is carried out using the mouse and keyboard. The mouse turns, the keyboard moves. Also from the keyboard is the management of the "Life". Since it takes more time to perceive three-dimensional space than it does for two-dimensional, it was decided to proceed to the next step by pressing a key.
The first tests visualizer passed with a bang. But when I tried to slip an array of 100 * 100 * 100 (or more, I do not remember exactly) cells, each frame was drawn up to 8 seconds. This is not the case. Then I remembered the visibility pyramid. Unfortunately, drawing on this very pyramid took almost the same time, since most of the time the space was completely visible. When approaching the center of this space and making the most of its movement, the rendering time decreased significantly.
There was still time, and the project was already ready for delivery. I realized that something was missing. But what exactly - the question is more complicated. After some time thinking, I decided that my KA is not at all like real life. There are not enough external factors that affect cell reproduction. As such a factor was chosen temperature.
In short, that is, a certain temperature, let's call it optimal, at which the survival rate and fertility are maximum. With decreasing and increasing temperatures, it becomes harder to survive. But just to set the temperature would not be interesting. And again we will resort to ka. In the initial state, the temperature is concentrated in the center of the space. Over time, "warm air" is evenly distributed throughout the space. This is achieved by diffusion. Yes, not simple, but integer. In this case, it is that some of the temperature in the cell remains, and the rest of the neighboring cells exchange. Such a cellular automaton can no longer be synchronous, since you were strange, if all the cells simultaneously changed ... And so that it could be programmed for several processes, it is necessary to resort to tricks - to move from asynchronous spacecraft to block-synchronous. The idea is that each process is allocated a block. Inside this unit, the spacecraft is asynchronous. But between the blocks are synchronized. In the picture, cells of the same color are calculated at the same time.

Of course, this implementation is not ideal. The code is not optimized. First of all, you can improve the visualizer. In addition to clipping on the pyramid of visibility, add clipping on the Z-buffer so that those cells that are hidden by the foreground cells are not drawn.
In general, the project can be inflated to a cosmic scale. For example, I want to add additional layers. If we talk only about external influences, then this may be, for example, relief. At higher altitudes, cells are less likely to be located. In addition, there will be colder. You can add a layer with vegetation that will serve as food. And you can clone a layer with the cells themselves and create several types of organisms that will eat each other. You can add mutations and much more. There would be a desire.
Now, finally, you can go to the most interesting.
At first, the program was tested without a temperature layer, since by that time it simply did not exist. Unfortunately, the program does not have a normal interface, and I had to write a test generator. He is of no particular interest. His only task is to make a cube of cells in the center of the playing space. Below are the cubes 3x3x3, 4x4x4 and 5x5x5. Here are just some of the steps to create a general picture of what is happening.
3x3x3, step 1:
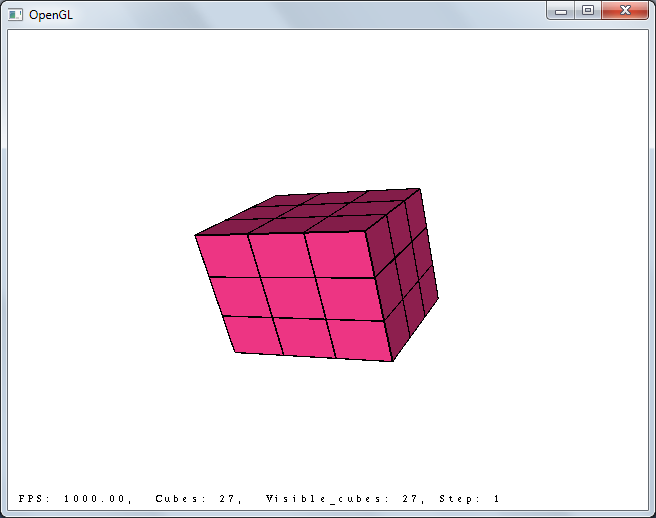
3x3x3, step 4:
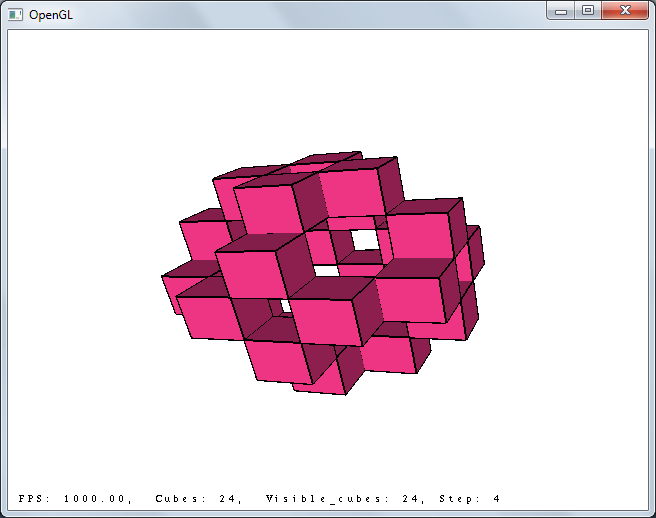
3x3x3, steps 5 and 6:
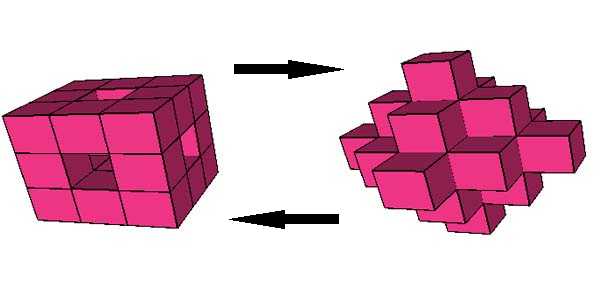
It turns out pretty funny flasher.
4x4x4, step 1:
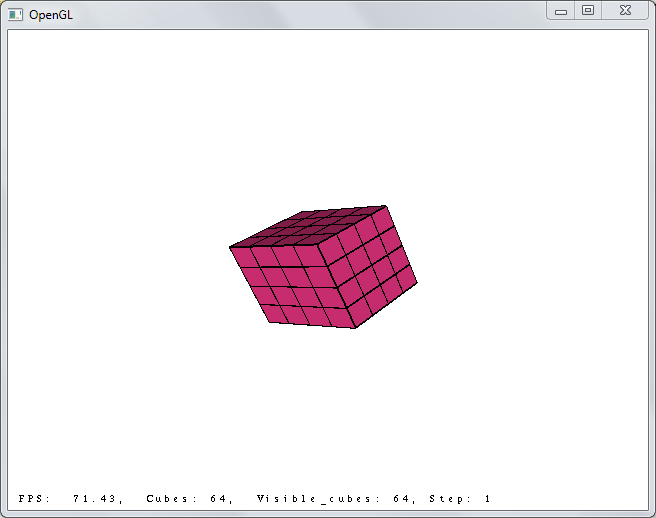
4x4x4, step 10:
4x4x4, step 100:
After that, almost nothing changes.
5x5x5, step 1:

5x5x5, step 4:
5x5x5, step 7:

5x5x5, step 8:
In the next step, not a single living cell remains.
Now add the temperature to the 4x4x4 cube. The temperature layer is presented in the form of a central slice. Red is the optimum temperature, yellow is just below normal, pink is low. The playing space has dimensions 50x50x50, in the center there is a cube 40x40x40 with the optimum temperature. That's what happened.
Step 1:

Step 10:
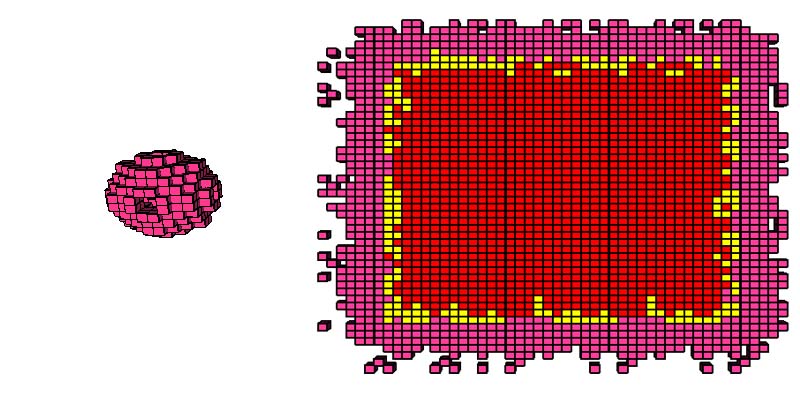
Step 50:

Step 150:

Step 200:

Everything is clear: the air cools down, life stops.
Unfortunately, I can’t share the program itself, since the input data is hard-coded in the generator. But I can share the source, but I warn you right away: the code is just awful.
Foreword
Last summer I had the opportunity to visit the summer school on parallel programming, conducted by the NSU. Within the school, each student had to prepare a project on one of the topics voiced at the lectures. I was interested in cellular automata. My first association with the phrase “cellular automaton” is “Life”.
I realized that no one would be interested to watch the black cells living on the screen. And it’s too easy for such a project. It was necessary to come up with something fundamentally new. I decided to expand the range of my thoughts and go beyond the limits of two-dimensional space. Literally. I thought, why not make this game three-dimensional? It's so much more interesting!
Stage 1. Cellular automaton
I think that here everyone (or almost everyone) imagines a cellular automaton. Therefore, we will not delve into the theory, but immediately proceed to practice. The only thing that distinguishes this cellular automaton from the most primitive is that it was necessary to parallelize the calculations. In the future, however, something else will be added, but for now let's not talk about it. The cellular automaton (hereinafter the KA) for our purposes should be synchronous. Fortunately, even with a parallel implementation of the algorithm, this does not create any inconvenience. When working with OpenMP, it is enough to simply place a loop that calculates the value of the spacecraft in the #pragma omp for {} block.
Like this
#pragma omp parallel shared(Temp, Space, Size) private(Num_of_nbr, x, y, z) { #pragma omp for for (x = 0; x < Size; x++) for (y = 0; y < Size; y++) for (z = 0; z < Size; z++) { // Neighbors(x, y, z) - // x, y z Num_of_nbr = Neighbors(x, y, z); if (Space[x][y][z] == 1) if (Num_of_nbr <= Smid + Sdiff * Koeff[Int_Temp[x][y][z]] \ && Num_of_nbr >= Smid - Sdiff * Koeff[Int_Temp[x][y][z]]) Temp[x][y][z] = 1; else Temp[x][y][z] = 0; else if (Num_of_nbr <= Bmid + Bdiff * Koeff[Int_Temp[x][y][z]] \ && Num_of_nbr >= Bmid - Bdiff * Koeff[Int_Temp[x][y][z]]) Temp[x][y][z] = 1; else Temp[x][y][z] = 0; } #pragma omp for for (x = 0; x < Size; x++) for (y = 0; y < Size; y++) for (z = 0; z < Size; z++) Space[x][y][z] = Temp[x][y][z]; } ')
Stage 2. Visualizer
It would not be bad if all this could be seen firsthand. And I was lucky, because literally a month before that I had little experience in working with OpenGL using the freeglut library. I also wanted the game space to be able to rotate, zoom in and out. Management is carried out using the mouse and keyboard. The mouse turns, the keyboard moves. Also from the keyboard is the management of the "Life". Since it takes more time to perceive three-dimensional space than it does for two-dimensional, it was decided to proceed to the next step by pressing a key.
The first tests visualizer passed with a bang. But when I tried to slip an array of 100 * 100 * 100 (or more, I do not remember exactly) cells, each frame was drawn up to 8 seconds. This is not the case. Then I remembered the visibility pyramid. Unfortunately, drawing on this very pyramid took almost the same time, since most of the time the space was completely visible. When approaching the center of this space and making the most of its movement, the rendering time decreased significantly.
Stage 3. External impacts
There was still time, and the project was already ready for delivery. I realized that something was missing. But what exactly - the question is more complicated. After some time thinking, I decided that my KA is not at all like real life. There are not enough external factors that affect cell reproduction. As such a factor was chosen temperature.
In short, that is, a certain temperature, let's call it optimal, at which the survival rate and fertility are maximum. With decreasing and increasing temperatures, it becomes harder to survive. But just to set the temperature would not be interesting. And again we will resort to ka. In the initial state, the temperature is concentrated in the center of the space. Over time, "warm air" is evenly distributed throughout the space. This is achieved by diffusion. Yes, not simple, but integer. In this case, it is that some of the temperature in the cell remains, and the rest of the neighboring cells exchange. Such a cellular automaton can no longer be synchronous, since you were strange, if all the cells simultaneously changed ... And so that it could be programmed for several processes, it is necessary to resort to tricks - to move from asynchronous spacecraft to block-synchronous. The idea is that each process is allocated a block. Inside this unit, the spacecraft is asynchronous. But between the blocks are synchronized. In the picture, cells of the same color are calculated at the same time.

Integer diffusion
#pragma omp parallel shared(Size, BlockSize, Int_Temp, PosCell, PosNbr, DiffKoeff)\ private(CellNum, NbrNum, x, y, z, Cell1, Cell2, Rem1, Rem2, Mov1, Mov2) { CellNum = rand() % 27; #pragma omp for for (x = 1; x < Size; x += BlockSize) for (y = 1; y < Size; y += BlockSize) for (z = 1; z < Size; z += BlockSize) { NbrNum = rand() % 6; Cell1 = Int_Temp[(x + PosCell[CellNum][0] + Size) % Size] \ [(y + PosCell[CellNum][1] + Size) % Size] \ [(z + PosCell[CellNum][2] + Size) % Size]; Cell2 = Int_Temp[(x +PosCell[CellNum][0] + PosNbr[NbrNum][0] + Size) % Size] \ [(y + PosCell[CellNum][1] + PosNbr[NbrNum][1] + Size) % Size] \ [(z + PosCell[CellNum][2] + PosNbr[NbrNum][2] + Size) % Size]; //DiffKoeff , // , . Rem1 = Cell1 * (float)(1.0 - DiffKoeff); Rem2 = Cell2 * (float)(1.0 - DiffKoeff); Mov1 = Cell1 * DiffKoeff; Mov2 = Cell2 * DiffKoeff; if ((float)Cell1 * DiffKoeff - (float)Mov1 > (float)(rand() % 10) / 10.0) Rem1++; else if ((float)Cell1 * DiffKoeff - (float)Mov1) Mov1++; if ((float)Cell2 * DiffKoeff - (float)Mov2 > (float)(rand() % 10) / 10.0) Rem2++; else if ((float)Cell2 * DiffKoeff - (float)Mov2) Mov2++; Int_Temp[(x + PosCell[CellNum][0] + Size) % Size] \ [(y + PosCell[CellNum][1] + Size) % Size] \ [(z + PosCell[CellNum][2] + Size) % Size] = Mov2 + Rem1; Int_Temp[(x +PosCell[CellNum][0] + PosNbr[NbrNum][0] + Size) % Size] \ [(y + PosCell[CellNum][1] + PosNbr[NbrNum][1] + Size) % Size] \ [(z + PosCell[CellNum][2] + PosNbr[NbrNum][2] + Size) % Size] \ = Mov1 + Rem2; } } Further prospects
Of course, this implementation is not ideal. The code is not optimized. First of all, you can improve the visualizer. In addition to clipping on the pyramid of visibility, add clipping on the Z-buffer so that those cells that are hidden by the foreground cells are not drawn.
In general, the project can be inflated to a cosmic scale. For example, I want to add additional layers. If we talk only about external influences, then this may be, for example, relief. At higher altitudes, cells are less likely to be located. In addition, there will be colder. You can add a layer with vegetation that will serve as food. And you can clone a layer with the cells themselves and create several types of organisms that will eat each other. You can add mutations and much more. There would be a desire.
results
Now, finally, you can go to the most interesting.
At first, the program was tested without a temperature layer, since by that time it simply did not exist. Unfortunately, the program does not have a normal interface, and I had to write a test generator. He is of no particular interest. His only task is to make a cube of cells in the center of the playing space. Below are the cubes 3x3x3, 4x4x4 and 5x5x5. Here are just some of the steps to create a general picture of what is happening.
3x3x3, step 1:

3x3x3, step 4:

3x3x3, steps 5 and 6:

It turns out pretty funny flasher.
4x4x4, step 1:

4x4x4, step 10:

4x4x4, step 100:

After that, almost nothing changes.
5x5x5, step 1:

5x5x5, step 4:

5x5x5, step 7:

5x5x5, step 8:

In the next step, not a single living cell remains.
Now add the temperature to the 4x4x4 cube. The temperature layer is presented in the form of a central slice. Red is the optimum temperature, yellow is just below normal, pink is low. The playing space has dimensions 50x50x50, in the center there is a cube 40x40x40 with the optimum temperature. That's what happened.
Step 1:

Step 10:

Step 50:

Step 150:

Step 200:

Everything is clear: the air cools down, life stops.
Unfortunately, I can’t share the program itself, since the input data is hard-coded in the generator. But I can share the source, but I warn you right away: the code is just awful.
Sources
Source: https://habr.com/ru/post/154753/
All Articles