Methods for calculating multinomial coefficients
One day, scrolling through the popular Q & A in mathematics ( math.stackexchange.com ), I discovered a question about calculating multinomial coefficients and he became interested in me. Note, for those who do not know what it is, there is an article in Wikipedia . So, we need to calculate the following expression:

It seemed, why on Habré lay out the solution to such a simple task? The answer is that the simplest naive method, consisting in multiplying the factorial of the sum and then dividing it by the product of factorials, will not work because intermediate calculations will go beyond the bit grid of the uint type and even ulong , although the result may be within values of these types. I liked this problem, and I immediately sat down to solve it and came up with three ways. I borrowed the other two ways from other answers. So, the article will be about the description and comparison of all the methods I implemented in C # under .NET.
Next, I will describe each method.
')
Of course, the first thing that came to mind was the use of a special type of BigInteger , capable of storing numbers with an arbitrary number of digits. But this, firstly, is not sporty, and, secondly, not all languages have support for these types (although of course you can write it yourself), but this method certainly always returns the correct result, unlike other methods that have rounding. By the way, this property allows you to test the accuracy of other methods, which will be discussed later.
The code of this method is no different from the naive implementation, except that BigInteger is everywhere instead of uint types. Therefore, of particular interest is not.
It consists in counting all the multinomial coefficients from the given arguments in Microsoft Excel, wolframalpha.com or other third-party programs / services and entering the calculated coefficients into the source code or a single file. The disadvantages of this approach are obvious: high memory consumption, the calculation of coefficients not from all the possible possible values of the arguments. Although the performance of this method, of course, on top. One way or another, this method was not even implemented by me.
This method consists in decomposing the expression of a multinomial coefficient into the product of several binomial coefficients according to the following formula:
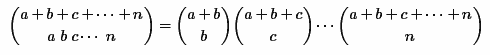
But here, again, overflow is possible already when calculating the last binomial coefficients. In order to prevent this from happening, a recursive calculation algorithm for each binomial coefficient is used according to the following formula:
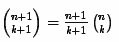
The C # code is as follows:
This method consists in decomposing the original formula into the sum and difference of logarithms as follows:
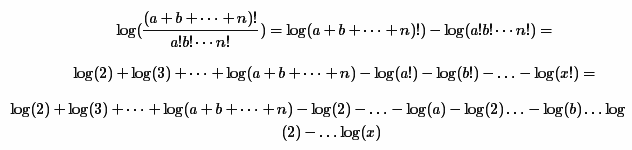
At the very end, of course, it is necessary to raise e to the degree obtained, which will be the result. A small optimization was also performed, which consisted in dropping the maximum factorial of the denominator from the numerator and denominator. In order to speed up subsequent calculations, all logarithms are cached into a list (at the end of the article, the performance of this optimization is tested).
This method does not differ much from the previous one, except that instead of decomposing the logarithm of factorial by the sum of logarithms, a special logarithm function from the gamma function is used, the implementation of which was taken from alglib . In fact, there are other, shorter implementations (for example, in Math.NET), but it seemed to me that if the size of the implementation code in alglib is the largest, the implementation itself is the most accurate.
My method is to apply a sequence of the following operations:
Testing of all methods took place in two stages: this is a test for the maximum number that can be calculated by any method without overflow and rounding errors, as well as a test for speed.
It is easy to prove that the multinomial coefficient is a commutative operation, i.e. for example, M (a, b, c) = M (a, c, b) = M (c, b, a), etc. So for checking all combinations of numbers with a given number of arguments, you can use permutations with repetitions . For these purposes, a library was used to generate data and other combinations of the codeproject . Thus, all the combinations were arranged in lexicographical order.
The two graphs below show the dependence of the number of permutation of the maximum possible computable number on the number of arguments in the multinomial function.
For a better understanding, I will explain the first set of values with the number of arguments 2:
In the test above, it is clear that, for example, the maximum ulong value that can be calculated using logarithms is 59481941558292. It was calculated from arguments 6 and 588, which corresponds to permutation 6481, if generated in the lexicographical order. This number is displayed on the green graph. The term rounding says that if we take the next permutation, i.e. (6.589), this method will consider a multinomial coefficient with an error of 1. And the term overflow says that if you calculate the coefficient from the next permutation (for example, if you take (1.63) for Binom ), then somewhere inside the method an overflow occurs .
Since the difference between the first and last permutation numbers is too large, I divided the graph into two parts (with the number of arguments 2-10 and 11-20). On twenty-one and more arguments, all functions give an incorrect result even on the first permutation (this is understandable, because Multinomial (1,1, ..., 1) = 21! And this number is greater than the maximum ulong . Further increase of any argument only increase the result. I will leave this statement without proof).
The orange graph shows the perfect result, i.e. generally the most maximal ulong that can only be computed by a multinomial function with a given number of arguments. Those. A further permutation increment will result in the result going beyond the ulong type. The values for this graph were calculated using large integers, which were discussed at the very beginning of the article.
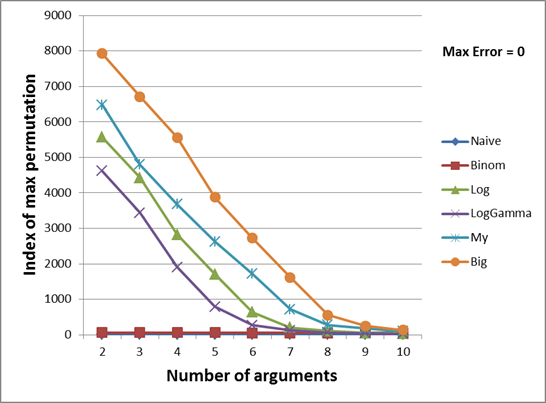
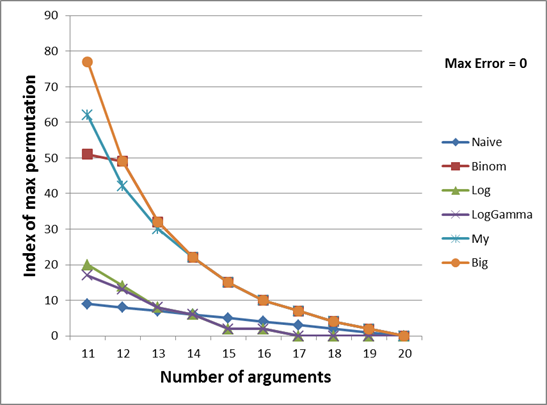
So, my method, as can be seen from both graphs, allows us to calculate a larger coefficient in almost all cases, with the exception of 12 and 13 arguments. Despite the high expectations of binomial coefficients, it turned out that they cover a small set of values in the case of a small number of them (from 2 to 8). Starting at 9, they begin to cover a larger range than Log and LogGamma , and at 12 and 13 they even bypass my method. After 13, they are calculated perfectly, however, as they are calculated, and my method.
The Log and LogGamma methods cover approximately the same range, especially with a large number of arguments. The fact that Log is still ahead of LogGamma by 1-12 is probably due to the fact that the Log (N!) Function is calculated less accurately than the sum of real numbers (logarithms). And the simple method even turned out to be more efficient than logarithms by 15-19 number of arguments.
It should be noted that the picture did not change much when the absolute error Max Error changed (i.e., the maximum permissible error during rounding), so I did not give other graphs with Max Error equal to 10 and 100.
For measuring the speed of each method, I used two test sets. The first covers fairly large numbers, on which the simple Naive method crashes with an overflow error, so it was not taken into account. BigInteger is also not taken into account. Each set was chased 20,000 times, and the given time of calculation was measured.
Also, these methods were tested with a preliminary calculation ( prefetch ) and without. This is relevant only for the Log and LogGamma methods , since only they use pre-calculated logarithms and logarithms from factorials.

As you can see, my method here turned out to be worse than the other methods every 3 times.
The fact that Binom calculated everything faster is explained by the fact that it uses only integer arithmetic, which is a priori faster.
A small advance of LogGamma compared to Log is explained by the fact that it does not add up logarithms again, but the logarithm of factorial, i.e. for example, instead of Ln (2) + Ln (3) + Ln (4), Ln (4!) is used.
It can also be seen that prefetch, as it turned out, has practically no effect on the Log and LogGamma speed , and this suggests that apparently calculating these functions is comparable to extracting the already calculated values or that the time to calculate them is too short compared to the total time remaining operations.
The following set was intended even for the simplest naive function. Larger numbers were also included in the following chart:

As you can see, in this case, my method showed a smaller lag from the rest of the functions (except for Big ), and the method with large numbers was 4 times worse than even my method. This is because the implementation of large numbers in .NET is far from ideal. Decompiling some of the System.Numerics library methods using ILSpy confirmed my assumptions (the code shows that even for such a simple operation as addition, a large amount of safe code is used):
Experiments have shown that my method turned out to be better than the others in the context of the most computable number (but still worse than ideal), but worse in the context of performance (but much better than the implementation with large numbers in .NET). You can also conclude that the implementation of the arithmetic of large numbers is far from ideal in .NET and if it is possible to replace it with another method, it is better to use it.
The method with binomial coefficients turned out to be the fastest, even faster than the simple implementation, but this is quite obvious, since it uses only integer arithmetic. On the other hand, this method does not cover such a large range of values, especially with a small number of arguments.
Also, experiments have shown that the reuse of calculated values of logarithms and logarithms from factorials does not give a significant performance gain, so that they can not be used.
I hope that the work done with the experiments will be interesting and useful not only for me, so I post the source code along with unit tests and tests on github: Multinimonal-Coefficient .
UPDATE

It seemed, why on Habré lay out the solution to such a simple task? The answer is that the simplest naive method, consisting in multiplying the factorial of the sum and then dividing it by the product of factorials, will not work because intermediate calculations will go beyond the bit grid of the uint type and even ulong , although the result may be within values of these types. I liked this problem, and I immediately sat down to solve it and came up with three ways. I borrowed the other two ways from other answers. So, the article will be about the description and comparison of all the methods I implemented in C # under .NET.
- Big numbers
- Tabular method
- Multiplication of binomial coefficients
- The sum and difference of logarithms
- The sum and difference of the functions of the "logarithm of factorial"
- My way
Next, I will describe each method.
')
Big numbers
Of course, the first thing that came to mind was the use of a special type of BigInteger , capable of storing numbers with an arbitrary number of digits. But this, firstly, is not sporty, and, secondly, not all languages have support for these types (although of course you can write it yourself), but this method certainly always returns the correct result, unlike other methods that have rounding. By the way, this property allows you to test the accuracy of other methods, which will be discussed later.
The code of this method is no different from the naive implementation, except that BigInteger is everywhere instead of uint types. Therefore, of particular interest is not.
BigInteger source
public static BigInteger BigAr(uint[] numbers) { BigInteger numbersSum = 0; foreach (var number in numbers) numbersSum += number; BigInteger nominator = Factorial(numbersSum); BigInteger denominator = 1; foreach (var number in numbers) denominator *= Factorial(new BigInteger(number)); return nominator / denominator; } public static BigInteger Factorial(BigInteger n) { BigInteger result = 1; for (ulong i = 1; i <= n; i++) result = result * i; return result; } Tabular method
It consists in counting all the multinomial coefficients from the given arguments in Microsoft Excel, wolframalpha.com or other third-party programs / services and entering the calculated coefficients into the source code or a single file. The disadvantages of this approach are obvious: high memory consumption, the calculation of coefficients not from all the possible possible values of the arguments. Although the performance of this method, of course, on top. One way or another, this method was not even implemented by me.
Binomial coefficients
This method consists in decomposing the expression of a multinomial coefficient into the product of several binomial coefficients according to the following formula:
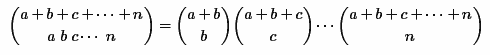
But here, again, overflow is possible already when calculating the last binomial coefficients. In order to prevent this from happening, a recursive calculation algorithm for each binomial coefficient is used according to the following formula:
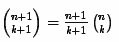
The C # code is as follows:
Binomial source
public static ulong BinomAr(uint[] numbers) { if (numbers.Length == 1) return 1; ulong result = 1; uint sum = numbers[0]; for (int i = 1; i < numbers.Length; i++) { sum += numbers[i]; result *= Binominal(sum, numbers[i]); } return result; } public static ulong Binominal(ulong n, ulong k) { ulong r = 1; ulong d; if (k > n) return 0; for (d = 1; d <= k; d++) { r *= n--; r /= d; } return r; } Logarithms
This method consists in decomposing the original formula into the sum and difference of logarithms as follows:
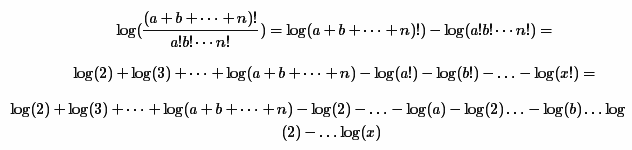
At the very end, of course, it is necessary to raise e to the degree obtained, which will be the result. A small optimization was also performed, which consisted in dropping the maximum factorial of the denominator from the numerator and denominator. In order to speed up subsequent calculations, all logarithms are cached into a list (at the end of the article, the performance of this optimization is tested).
Log source
static List<double> Logarithms = new List<double>(); public static ulong Log(params uint[] numbers) { return LogAr(numbers); } public static ulong LogAr(uint[] numbers) { int maxNumber = (int)numbers.Max(); uint numbersSum = 0; foreach (var number in numbers) numbersSum += number; double sum = 0; for (int i = 2; i <= numbersSum; i++) { if (i <= maxNumber) { if (i - 2 >= Logarithms.Count) { var log = Math.Log(i); Logarithms.Add(log); } } else { if (i - 2 < Logarithms.Count) sum += Logarithms[i - 2]; else { var log = Math.Log(i); Logarithms.Add(log); sum += log; } } } var maxNumberFirst = false; foreach (var number in numbers) if (number == maxNumber && !maxNumberFirst) maxNumberFirst = true; else for (int i = 2; i <= number; i++) sum -= Logarithms[i - 2]; return (ulong)Math.Round(Math.Exp(sum)); } Logarithms from factorials
This method does not differ much from the previous one, except that instead of decomposing the logarithm of factorial by the sum of logarithms, a special logarithm function from the gamma function is used, the implementation of which was taken from alglib . In fact, there are other, shorter implementations (for example, in Math.NET), but it seemed to me that if the size of the implementation code in alglib is the largest, the implementation itself is the most accurate.
LogGamma source
static Dictionary<uint, double> LnFacts = new Dictionary<uint, double>(); public static ulong LogGammaAr(uint[] numbers) { int maxNumber = (int)numbers.Max(); double value; double denom = 0; uint numbersSum = 0; foreach (var number in numbers) { numbersSum += number; if (LnFacts.TryGetValue(number, out value)) denom += value; else { value = LnGamma(number + 1); LnFacts.Add(number, value); denom += value; } } double numer; if (LnFacts.TryGetValue(numbersSum, out value)) numer = value; else { value = LnGamma(numbersSum + 1); LnFacts.Add(numbersSum, value); numer = value; } return (ulong)Math.Round(Math.Exp(numer - denom)); } public static double LnGamma(double x) { double sign = 1; return LnGamma(x, ref sign); } public static double LnGamma(double x, ref double sgngam) { double result = 0; double a = 0; double b = 0; double c = 0; double p = 0; double q = 0; double u = 0; double w = 0; double z = 0; int i = 0; double logpi = 0; double ls2pi = 0; double tmp = 0; sgngam = 0; sgngam = 1; logpi = 1.14472988584940017414; ls2pi = 0.91893853320467274178; if ((double)(x) < (double)(-34.0)) { q = -x; w = LnGamma(q, ref tmp); p = (int)Math.Floor(q); i = (int)Math.Round(p); if (i % 2 == 0) { sgngam = -1; } else { sgngam = 1; } z = q - p; if ((double)(z) > (double)(0.5)) { p = p + 1; z = p - q; } z = q * Math.Sin(Math.PI * z); result = logpi - Math.Log(z) - w; return result; } if ((double)(x) < (double)(13)) { z = 1; p = 0; u = x; while ((double)(u) >= (double)(3)) { p = p - 1; u = x + p; z = z * u; } while ((double)(u) < (double)(2)) { z = z / u; p = p + 1; u = x + p; } if ((double)(z) < (double)(0)) { sgngam = -1; z = -z; } else { sgngam = 1; } if ((double)(u) == (double)(2)) { result = Math.Log(z); return result; } p = p - 2; x = x + p; b = -1378.25152569120859100; b = -38801.6315134637840924 + x * b; b = -331612.992738871184744 + x * b; b = -1162370.97492762307383 + x * b; b = -1721737.00820839662146 + x * b; b = -853555.664245765465627 + x * b; c = 1; c = -351.815701436523470549 + x * c; c = -17064.2106651881159223 + x * c; c = -220528.590553854454839 + x * c; c = -1139334.44367982507207 + x * c; c = -2532523.07177582951285 + x * c; c = -2018891.41433532773231 + x * c; p = x * b / c; result = Math.Log(z) + p; return result; } q = (x - 0.5) * Math.Log(x) - x + ls2pi; if ((double)(x) > (double)(100000000)) { result = q; return result; } p = 1 / (x * x); if ((double)(x) >= (double)(1000.0)) { q = q + ((7.9365079365079365079365 * 0.0001 * p - 2.7777777777777777777778 * 0.001) * p + 0.0833333333333333333333) / x; } else { a = 8.11614167470508450300 * 0.0001; a = -(5.95061904284301438324 * 0.0001) + p * a; a = 7.93650340457716943945 * 0.0001 + p * a; a = -(2.77777777730099687205 * 0.001) + p * a; a = 8.33333333333331927722 * 0.01 + p * a; q = q + a / x; } result = q; return result; } My method
My method is to apply a sequence of the following operations:
- Counting the powers of the numbers in the denominator. For example, for arguments (5, 5, 5) they will be as follows: denomFactorPowers [6] = {0, 0, 2, 2, 2, 2}. Those. If you multiply all factorials in the denominator, you get 3 ^ 2 * 4 ^ 2 * 5 ^ 2 * 6 ^ 2. And the degree is exactly the second, because part of the degrees was reduced with the numerator, and in the numerator it became 6 * ... * 15, instead of 1 * ... * 15.
- Initialization result = 1 (result of the function); tempDenom = 1 (the result of multiplying the numbers in the denominator); currentFactor (current factor in the denominator).
- The cycle of the variable i over all the remaining numerators of the numerator (maxNumber + 1 ... numbersSum) .
- Calculate tempDenom until tempDenom < result and the denominator have run out of numbers (currentFactor <denomFactorPowers.Length) .
- If tempDenom> result or the denominator ran out of numbers (currentFactor> = denomFactorPowers.Length) , then calculate the result as follows: result = result / tempDenom * i . This technique allows you to calculate the result as accurately as possible and without overflow, because result / tempDenom → 1 .
My method source
public static ulong MyAr(uint[] numbers) { uint numbersSum = 0; foreach (var number in numbers) numbersSum += number; uint maxNumber = numbers.Max(); var denomFactorPowers = new uint[maxNumber + 1]; foreach (var number in numbers) for (int i = 2; i <= number; i++) denomFactorPowers[i]++; for (int i = 2; i < denomFactorPowers.Length; i++) denomFactorPowers[i]--; // reduce with nominator; uint currentFactor = 2; uint currentPower = 1; double result = 1; for (uint i = maxNumber + 1; i <= numbersSum; i++) { uint tempDenom = 1; while (tempDenom < result && currentFactor < denomFactorPowers.Length) { if (currentPower > denomFactorPowers[currentFactor]) { currentFactor++; currentPower = 1; } else { tempDenom *= currentFactor; currentPower++; } } result = result / tempDenom * i; } return (ulong)Math.Round(result); } Testing
Testing of all methods took place in two stages: this is a test for the maximum number that can be calculated by any method without overflow and rounding errors, as well as a test for speed.
Test for the highest possible computable number
It is easy to prove that the multinomial coefficient is a commutative operation, i.e. for example, M (a, b, c) = M (a, c, b) = M (c, b, a), etc. So for checking all combinations of numbers with a given number of arguments, you can use permutations with repetitions . For these purposes, a library was used to generate data and other combinations of the codeproject . Thus, all the combinations were arranged in lexicographical order.
The two graphs below show the dependence of the number of permutation of the maximum possible computable number on the number of arguments in the multinomial function.
For a better understanding, I will explain the first set of values with the number of arguments 2:
Arg count: 2 Naive(1,19) = 20; #18; overflow Binom(1,61) = 62; #60; overflow LogGamma(5,623) = 801096582000; #4612; rounding(error = 1) Log(6,588) = 59481941558292; #5572; rounding(error = 1) My(7,503) = 1708447057008120; #6481; rounding(error = 1) Big(8,959) = 18419736117819661560; #7930 In the test above, it is clear that, for example, the maximum ulong value that can be calculated using logarithms is 59481941558292. It was calculated from arguments 6 and 588, which corresponds to permutation 6481, if generated in the lexicographical order. This number is displayed on the green graph. The term rounding says that if we take the next permutation, i.e. (6.589), this method will consider a multinomial coefficient with an error of 1. And the term overflow says that if you calculate the coefficient from the next permutation (for example, if you take (1.63) for Binom ), then somewhere inside the method an overflow occurs .
Since the difference between the first and last permutation numbers is too large, I divided the graph into two parts (with the number of arguments 2-10 and 11-20). On twenty-one and more arguments, all functions give an incorrect result even on the first permutation (this is understandable, because Multinomial (1,1, ..., 1) = 21! And this number is greater than the maximum ulong . Further increase of any argument only increase the result. I will leave this statement without proof).
The orange graph shows the perfect result, i.e. generally the most maximal ulong that can only be computed by a multinomial function with a given number of arguments. Those. A further permutation increment will result in the result going beyond the ulong type. The values for this graph were calculated using large integers, which were discussed at the very beginning of the article.


So, my method, as can be seen from both graphs, allows us to calculate a larger coefficient in almost all cases, with the exception of 12 and 13 arguments. Despite the high expectations of binomial coefficients, it turned out that they cover a small set of values in the case of a small number of them (from 2 to 8). Starting at 9, they begin to cover a larger range than Log and LogGamma , and at 12 and 13 they even bypass my method. After 13, they are calculated perfectly, however, as they are calculated, and my method.
The Log and LogGamma methods cover approximately the same range, especially with a large number of arguments. The fact that Log is still ahead of LogGamma by 1-12 is probably due to the fact that the Log (N!) Function is calculated less accurately than the sum of real numbers (logarithms). And the simple method even turned out to be more efficient than logarithms by 15-19 number of arguments.
It should be noted that the picture did not change much when the absolute error Max Error changed (i.e., the maximum permissible error during rounding), so I did not give other graphs with Max Error equal to 10 and 100.
Performance test methods
For measuring the speed of each method, I used two test sets. The first covers fairly large numbers, on which the simple Naive method crashes with an overflow error, so it was not taken into account. BigInteger is also not taken into account. Each set was chased 20,000 times, and the given time of calculation was measured.
Also, these methods were tested with a preliminary calculation ( prefetch ) and without. This is relevant only for the Log and LogGamma methods , since only they use pre-calculated logarithms and logarithms from factorials.
The first test argument set
(1, 1) (1, 2) (2, 1) (2, 2) (5, 5, 5) (10, 10, 10) (5, 10, 15) (6, 6, 6, 6) (5, 6, 7, 8) (2, 3, 4, 5, 7) 
As you can see, my method here turned out to be worse than the other methods every 3 times.
The fact that Binom calculated everything faster is explained by the fact that it uses only integer arithmetic, which is a priori faster.
A small advance of LogGamma compared to Log is explained by the fact that it does not add up logarithms again, but the logarithm of factorial, i.e. for example, instead of Ln (2) + Ln (3) + Ln (4), Ln (4!) is used.
It can also be seen that prefetch, as it turned out, has practically no effect on the Log and LogGamma speed , and this suggests that apparently calculating these functions is comparable to extracting the already calculated values or that the time to calculate them is too short compared to the total time remaining operations.
Second test argument set
The following set was intended even for the simplest naive function. Larger numbers were also included in the following chart:
(1, 1) (1, 2) (2, 1) (2, 2) (5, 5, 5) (1, 1, 1, 1, 1, 1, 1, 1, 2) (1, 2, 3, 4, 5, 4) 
As you can see, in this case, my method showed a smaller lag from the rest of the functions (except for Big ), and the method with large numbers was 4 times worse than even my method. This is because the implementation of large numbers in .NET is far from ideal. Decompiling some of the System.Numerics library methods using ILSpy confirmed my assumptions (the code shows that even for such a simple operation as addition, a large amount of safe code is used):
Add operation for BigInteger in .NET
public static BigInteger operator +(BigInteger left, BigInteger right) { if (right.IsZero) { return left; } if (left.IsZero) { return right; } int num = 1; int num2 = 1; BigIntegerBuilder bigIntegerBuilder = new BigIntegerBuilder(left, ref num); BigIntegerBuilder bigIntegerBuilder2 = new BigIntegerBuilder(right, ref num2); if (num == num2) { bigIntegerBuilder.Add(ref bigIntegerBuilder2); } else { bigIntegerBuilder.Sub(ref num, ref bigIntegerBuilder2); } return bigIntegerBuilder.GetInteger(num); } ... public void Add(ref BigIntegerBuilder reg) { if (reg._iuLast == 0) { this.Add(reg._uSmall); return; } if (this._iuLast != 0) { this.EnsureWritable(Math.Max(this._iuLast, reg._iuLast) + 1, 1); int num = reg._iuLast + 1; if (this._iuLast < reg._iuLast) { num = this._iuLast + 1; Array.Copy(reg._rgu, this._iuLast + 1, this._rgu, this._iuLast + 1, reg._iuLast - this._iuLast); this._iuLast = reg._iuLast; } uint num2 = 0u; for (int i = 0; i < num; i++) { num2 = BigIntegerBuilder.AddCarry(ref this._rgu[i], reg._rgu[i], num2); } if (num2 != 0u) { this.ApplyCarry(num); } return; } uint uSmall = this._uSmall; if (uSmall == 0u) { this = new BigIntegerBuilder(ref reg); return; } this.Load(ref reg, 1); this.Add(uSmall); } Conclusion
Experiments have shown that my method turned out to be better than the others in the context of the most computable number (but still worse than ideal), but worse in the context of performance (but much better than the implementation with large numbers in .NET). You can also conclude that the implementation of the arithmetic of large numbers is far from ideal in .NET and if it is possible to replace it with another method, it is better to use it.
The method with binomial coefficients turned out to be the fastest, even faster than the simple implementation, but this is quite obvious, since it uses only integer arithmetic. On the other hand, this method does not cover such a large range of values, especially with a small number of arguments.
Also, experiments have shown that the reuse of calculated values of logarithms and logarithms from factorials does not give a significant performance gain, so that they can not be used.
I hope that the work done with the experiments will be interesting and useful not only for me, so I post the source code along with unit tests and tests on github: Multinimonal-Coefficient .
UPDATE
- Updated the method with binomial coefficients: link , author: Mrrl
- Added method with decomposition into powers of primes: link , author: Mrrl
- Added a method with the calculation of combinations of coefficients obtained by decomposing the degree of the sum into the following terms: description and source
Source: https://habr.com/ru/post/153255/
All Articles