Local Binary Patterns operator in the texture classification task
Hello, dear habrakrady!
In this article I would like to talk about a relatively new operator used in the problem of texture classification. This task is very close to the task of finding, recognizing and classifying images.
The LBP operator can be used to search for an object in an image (for example, a face), as well as to check that this object belongs to a certain class (verification, recognition of emotions, gender by face). Interested mercy I ask under cat.
The LBP operator was first proposed by T.Ojala in 1996. It is an efficient operator that represents each pixel of an image as a binary number, depending on the intensities of the neighboring pixels of the image.
')
This operator is computationally efficient, since it only works with integer arithmetic (this allows real-time performance in some tasks), and it is also invariant to changes in brightness in the image caused by shooting in various lighting conditions.
What is LBP? Classic LBP, which is applied to an image pixel, uses eight pixels of a neighborhood.
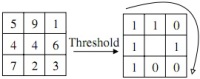
It takes the center pixel as a threshold and compares the brightness value in each pixel of the neighborhood with it. If this value is greater than the threshold (or equal value), then the pixel takes the value 1. If less than - 0. The resulting eight-bit number characterizes the neighborhood of the pixel. Total variants of such numbers 2 ^ 8 = 256. Thus, we assigned each pixel of the image one of the 256 labels characterizing it. Further, it is not difficult to construct a histogram from these data and compare textures using LBP histograms.
However, I would like to use a neighborhood of an arbitrary radius with an arbitrary number of significant pixels. In 2002, the eLBP (extended LBP) method was proposed, which satisfies these conditions. Now the neighborhood looks like this:

To find the brightness value at points of an arbitrary pixel neighborhood, bilinear interpolation is used. That is, the point is assigned an average weighted value of the neighboring pixels. The rest of the method works in the same way as the classic LBP.
However, it is clear that with an increase in the neighborhood, the number of digits in the numbers with which work is required increases. That is, for a neighborhood of radius 2 of 16 dots, it is required to work with numbers consisting of 16 bits. And the number of histogram bins becomes huge. After some time, it was found out that the most information is carried by the so-called uniform patterns (unfortunately I could not translate it into Russian so that my hearing would not hurt) . The bottom line is that these patterns contain no more than a certain number of transitions from 0 to 1 in the record and vice versa. That is, the numbers 00011000 or 00000000 will be uniform patterns, and 00100100 will not, if the specified number of transitions is two (000 transition 11 transition 000 - uniform (2 transitions), 00 transition 1 transition 100 transition 1 transition 00 - no (4 transitions).
The LBP operator is used as part of many classifiers. The simplest application is to create histograms and compare them (I briefly touched on this method). It is also used with machine learning algorithms such as SVM and AdaBoost. And if the public is interested in these methods, this will be a good motivation for writing a new article.
Thank you so much for your attention, I hope that my style of presentation was simple enough to understand.
- Literature:
Zhiguang Yang and Haizhou Ai - Demographic Classification with Local Binary Patterns
In this article I would like to talk about a relatively new operator used in the problem of texture classification. This task is very close to the task of finding, recognizing and classifying images.
The LBP operator can be used to search for an object in an image (for example, a face), as well as to check that this object belongs to a certain class (verification, recognition of emotions, gender by face). Interested mercy I ask under cat.
The LBP operator was first proposed by T.Ojala in 1996. It is an efficient operator that represents each pixel of an image as a binary number, depending on the intensities of the neighboring pixels of the image.
')
This operator is computationally efficient, since it only works with integer arithmetic (this allows real-time performance in some tasks), and it is also invariant to changes in brightness in the image caused by shooting in various lighting conditions.
What is LBP? Classic LBP, which is applied to an image pixel, uses eight pixels of a neighborhood.

It takes the center pixel as a threshold and compares the brightness value in each pixel of the neighborhood with it. If this value is greater than the threshold (or equal value), then the pixel takes the value 1. If less than - 0. The resulting eight-bit number characterizes the neighborhood of the pixel. Total variants of such numbers 2 ^ 8 = 256. Thus, we assigned each pixel of the image one of the 256 labels characterizing it. Further, it is not difficult to construct a histogram from these data and compare textures using LBP histograms.
However, I would like to use a neighborhood of an arbitrary radius with an arbitrary number of significant pixels. In 2002, the eLBP (extended LBP) method was proposed, which satisfies these conditions. Now the neighborhood looks like this:

To find the brightness value at points of an arbitrary pixel neighborhood, bilinear interpolation is used. That is, the point is assigned an average weighted value of the neighboring pixels. The rest of the method works in the same way as the classic LBP.
However, it is clear that with an increase in the neighborhood, the number of digits in the numbers with which work is required increases. That is, for a neighborhood of radius 2 of 16 dots, it is required to work with numbers consisting of 16 bits. And the number of histogram bins becomes huge. After some time, it was found out that the most information is carried by the so-called uniform patterns (unfortunately I could not translate it into Russian so that my hearing would not hurt) . The bottom line is that these patterns contain no more than a certain number of transitions from 0 to 1 in the record and vice versa. That is, the numbers 00011000 or 00000000 will be uniform patterns, and 00100100 will not, if the specified number of transitions is two (000 transition 11 transition 000 - uniform (2 transitions), 00 transition 1 transition 100 transition 1 transition 00 - no (4 transitions).
The LBP operator is used as part of many classifiers. The simplest application is to create histograms and compare them (I briefly touched on this method). It is also used with machine learning algorithms such as SVM and AdaBoost. And if the public is interested in these methods, this will be a good motivation for writing a new article.
Thank you so much for your attention, I hope that my style of presentation was simple enough to understand.
- Literature:
Zhiguang Yang and Haizhou Ai - Demographic Classification with Local Binary Patterns
Source: https://habr.com/ru/post/153109/
All Articles