Theory of complexity with simple examples
Ask the question "WHERE?". Where is the center of motion control of galaxies or cyclone behavior? Where is the power that unites atoms into complex compounds, they, in turn, into chains of proteins, and gives rise to such stable and complex phenomena as biological life, mind, society.
Under the umbrella of the theory of complexity, various models are combined that describe how, without central control, from the interaction of simple initial elements obeying simple rules, phenomena of a higher order are formed, possessing difficultly predictable behavior and unforeseen, but stable, properties.
The article does not offer ready-made answers about the meaning of life, it shows through crude non-strict analogies, but at the same time it has the audacious goal to broaden the reader’s outlook, relying on his imagination and some mathematical facts.
First, let's be clear on how complex unpredictable behavior can arise based on a simple deterministic rule. Meet the "Logistic Map":
x n + 1 = Rx n (1 - x n )
')
I hasten to pre-empt possible thought “Well, that is dull! Now there will be formulas ... ". Try to understand, it will be very interesting.
Logistic Map - describes an iterative process in which the next value of a function is analytically determined by its value at the previous step. We plot the graphs of this function for different values of the “R” coefficient, taking the initial value X 0 = 0.1
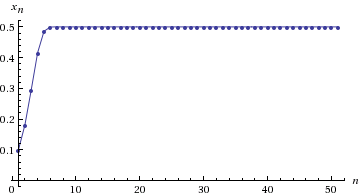
1) R = 2. The graph degenerates into the line:
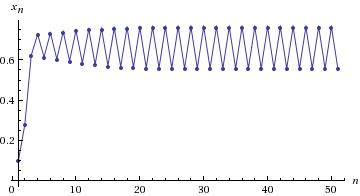
2) R = 3.1. Comes to oscillation state between 2 values:
3) R = 3.47. Oscillation frequency 4:

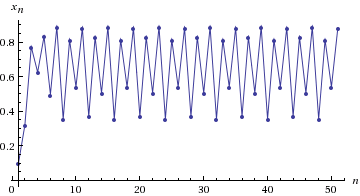
4) R = 3.55. Oscillation frequency 8:
5) And now R = 3.999:
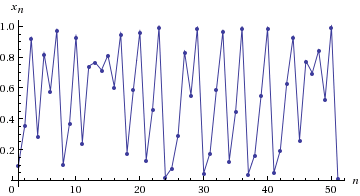
There are no regularities in this graph. When R = 3.999, we observe chaos. Under the chaos understand the extreme sensitivity of the final result in relation to the initial data. Let's change the initial value X 0 = 0.1000000001 (one in 10 characters) and plot the graph in red over the previous result.

This picture may serve as an illustration of the so-called. "Butterfly effect". As a result of a slight change in the initial value of 10 digits after the comma, already at 30 iterations we get a completely different graph. This property is so remarkable that it is used in pseudo-random number generators.
We will get completely different graphs by constructing them for a certain irrational number, calculated with different (extremely insignificant) accuracy. Don't take my word for it, take it (1 / sqrt (2)) and go for it!
Thus, we have learned that complex chaotic behavior, seemingly random, can occur in systems based on simple deterministic rules. Moreover, this behavior cannot be predicted in the long term due to the strong sensitivity of the behavior to the initial conditions (or inaccuracies in physical measurements).
Let's look at another interesting example - cellular automata, and in particular, John Conway's game “Life” .
The rules of the game set only the behavior of a single cell among the nearest neighbors. However, we have that in the gaming cellular environment without any initial prescription, stable phenomena of a higher order arise. The life of individual cells, which are strictly tied to their positions, generates persistent disturbances in the environment, called patterns. Perturbations may be static, oscillating, or exhibiting more complex behavior. For example, move and collide, collapsing or generating new formations with bizarre properties.
A few pictures from Wikipedia to maintain interest:
Such properties or phenomena that were not explicitly specified initially, but resulting from the interaction processes of the original components, are called emergent (literally, arising). These properties are created and maintained by processes within the environment. As soon as the processes disappear - the properties also disappear, as life disappears if you disassemble the body into its components, and then mechanically try to put it together.
Emergent properties are an integral feature of complex systems.
Dive deeper and turn to the work of Stephen Wolfram , published in the book "New Kind of Science".
Tungsten conducted experiments with the simplest version of the game life, in which the medium is a long closed tape with a width of one cell. They were driven by the idea that if it is impossible to understand what is happening in this very simple cellular automaton, then there is nothing more to think about more complex systems.
The rules are simple. A cell can be alive or dead depending on its previous state and the state of its two neighbors. Total, the subsequent state of the cell is determined by three parameters.
Now be patient - we practice in combinatorics ...
Of the possible states of the 3 cells, only 8 possible combinations can be made.
Each combination can translate a cell into one of 2 possible states (on and off). In total, there is a small finite number of possible rules: 256 (2 8 ).
On each rule, Wolfram conducted a series of experiments with various initial data and, as a result, singled out 4 classes of rules:
1) Almost all initial configurations are set to the same final pattern.
2) Almost all initial configurations are set in the same final pattern or circulate between several final patterns.
3) Most of the initial configurations create random-looking behavior and also generate triangles or other regular structures.
4) The last class combines order and randomness, giving rise to localized structures that, being simple in themselves, move and interact with each other in a very complex way.
Picture to maintain attention:

Grade 4 is the most interesting. An example of a class 4 rule is “rule 110” , illustrated above.
There is something unexpected about him. A student of Wolfram, Matthew Cook, proved that ... (drumming ...) this rule is Turing-complete. In other words - this is the simplest known at the moment computational model.
Wolfram suggested that some such simple rule may underlie all the laws of nature. According to him, the world is a complex system generated by this simple rule on a certain universal cellular automaton from the big bang to the instant you read these lines.
This statement rests on the sacred debate about whether the universe is computable or computing is only a mental model that allows us to describe with some precision the trace of "something happening somehow."
The article describes only a few basic models of the theory of complexity. These formalisms allow us to explain how from the behavior of the simplest basic elements can arise complex phenomena at the level of the whole system.
I have not touched upon the models of evolution, adaptation, social self-organization based on game theory and network theory. If the article finds a response - perhaps I will write another one, where I will try to cover these aspects as well.
Some companies are adopting self-organization, as a way of existence of social organization. That is, by abandoning central control, they give the individual complete freedom to choose what to do: join a ready-made project group or, starting a project, search and inspire like-minded people. You can find an analogy with the immune system, attacking viruses - interesting tasks find their performers. As long as the vector of the specialist’s activities coincides with the vector of the company - everything goes for future, otherwise the social system will reject the foreign body :)
Also, some models of the theory of complexity underlie flexible development methodologies , where, unlike waterfall, the system is not specified fully in advance, but flexibly adapts to external requirements.
Complexity. A guided tour
New Kind of Science
Complexity Theory for Software Developers
Video: Stanford lectures. Emergence and Complexity
Video: NKS Presentation by Stephen Wolfram
Video: the universe as a cellular automaton
Corporate culture at Valve
Under the umbrella of the theory of complexity, various models are combined that describe how, without central control, from the interaction of simple initial elements obeying simple rules, phenomena of a higher order are formed, possessing difficultly predictable behavior and unforeseen, but stable, properties.
The article does not offer ready-made answers about the meaning of life, it shows through crude non-strict analogies, but at the same time it has the audacious goal to broaden the reader’s outlook, relying on his imagination and some mathematical facts.
Predictable unpredictability
First, let's be clear on how complex unpredictable behavior can arise based on a simple deterministic rule. Meet the "Logistic Map":
x n + 1 = Rx n (1 - x n )
')
I hasten to pre-empt possible thought “Well, that is dull! Now there will be formulas ... ". Try to understand, it will be very interesting.
Logistic Map - describes an iterative process in which the next value of a function is analytically determined by its value at the previous step. We plot the graphs of this function for different values of the “R” coefficient, taking the initial value X 0 = 0.1
1) R = 2. The graph degenerates into the line:

2) R = 3.1. Comes to oscillation state between 2 values:

3) R = 3.47. Oscillation frequency 4:

4) R = 3.55. Oscillation frequency 8:

5) And now R = 3.999:

There are no regularities in this graph. When R = 3.999, we observe chaos. Under the chaos understand the extreme sensitivity of the final result in relation to the initial data. Let's change the initial value X 0 = 0.1000000001 (one in 10 characters) and plot the graph in red over the previous result.

This picture may serve as an illustration of the so-called. "Butterfly effect". As a result of a slight change in the initial value of 10 digits after the comma, already at 30 iterations we get a completely different graph. This property is so remarkable that it is used in pseudo-random number generators.
We will get completely different graphs by constructing them for a certain irrational number, calculated with different (extremely insignificant) accuracy. Don't take my word for it, take it (1 / sqrt (2)) and go for it!
Thus, we have learned that complex chaotic behavior, seemingly random, can occur in systems based on simple deterministic rules. Moreover, this behavior cannot be predicted in the long term due to the strong sensitivity of the behavior to the initial conditions (or inaccuracies in physical measurements).
Game "Life"
Let's look at another interesting example - cellular automata, and in particular, John Conway's game “Life” .
The rules of the game set only the behavior of a single cell among the nearest neighbors. However, we have that in the gaming cellular environment without any initial prescription, stable phenomena of a higher order arise. The life of individual cells, which are strictly tied to their positions, generates persistent disturbances in the environment, called patterns. Perturbations may be static, oscillating, or exhibiting more complex behavior. For example, move and collide, collapsing or generating new formations with bizarre properties.
A few pictures from Wikipedia to maintain interest:
 |  |  |
Such properties or phenomena that were not explicitly specified initially, but resulting from the interaction processes of the original components, are called emergent (literally, arising). These properties are created and maintained by processes within the environment. As soon as the processes disappear - the properties also disappear, as life disappears if you disassemble the body into its components, and then mechanically try to put it together.
Emergent properties are an integral feature of complex systems.
Steven Wolfram cellular automata and the “rule 110”
Dive deeper and turn to the work of Stephen Wolfram , published in the book "New Kind of Science".
Tungsten conducted experiments with the simplest version of the game life, in which the medium is a long closed tape with a width of one cell. They were driven by the idea that if it is impossible to understand what is happening in this very simple cellular automaton, then there is nothing more to think about more complex systems.
The rules are simple. A cell can be alive or dead depending on its previous state and the state of its two neighbors. Total, the subsequent state of the cell is determined by three parameters.
Now be patient - we practice in combinatorics ...
Of the possible states of the 3 cells, only 8 possible combinations can be made.

Each combination can translate a cell into one of 2 possible states (on and off). In total, there is a small finite number of possible rules: 256 (2 8 ).
On each rule, Wolfram conducted a series of experiments with various initial data and, as a result, singled out 4 classes of rules:
1) Almost all initial configurations are set to the same final pattern.
2) Almost all initial configurations are set in the same final pattern or circulate between several final patterns.
3) Most of the initial configurations create random-looking behavior and also generate triangles or other regular structures.
4) The last class combines order and randomness, giving rise to localized structures that, being simple in themselves, move and interact with each other in a very complex way.
Picture to maintain attention:

Grade 4 is the most interesting. An example of a class 4 rule is “rule 110” , illustrated above.

There is something unexpected about him. A student of Wolfram, Matthew Cook, proved that ... (drumming ...) this rule is Turing-complete. In other words - this is the simplest known at the moment computational model.
Wolfram suggested that some such simple rule may underlie all the laws of nature. According to him, the world is a complex system generated by this simple rule on a certain universal cellular automaton from the big bang to the instant you read these lines.
This statement rests on the sacred debate about whether the universe is computable or computing is only a mental model that allows us to describe with some precision the trace of "something happening somehow."
Conclusion
The article describes only a few basic models of the theory of complexity. These formalisms allow us to explain how from the behavior of the simplest basic elements can arise complex phenomena at the level of the whole system.
I have not touched upon the models of evolution, adaptation, social self-organization based on game theory and network theory. If the article finds a response - perhaps I will write another one, where I will try to cover these aspects as well.
Some companies are adopting self-organization, as a way of existence of social organization. That is, by abandoning central control, they give the individual complete freedom to choose what to do: join a ready-made project group or, starting a project, search and inspire like-minded people. You can find an analogy with the immune system, attacking viruses - interesting tasks find their performers. As long as the vector of the specialist’s activities coincides with the vector of the company - everything goes for future, otherwise the social system will reject the foreign body :)
Also, some models of the theory of complexity underlie flexible development methodologies , where, unlike waterfall, the system is not specified fully in advance, but flexibly adapts to external requirements.
Recommended Sources
Complexity. A guided tour
New Kind of Science
Complexity Theory for Software Developers
Video: Stanford lectures. Emergence and Complexity
Video: NKS Presentation by Stephen Wolfram
Video: the universe as a cellular automaton
Corporate culture at Valve
Source: https://habr.com/ru/post/152153/
All Articles