CUDA: block synchronization
When using parallel computing, it is very likely that a situation may arise when the algorithm contains two such sequential steps: i ) each jth stream stores some intermediate calculation result in the jth memory cell, and then ii ) this stream should use the results of one or more "neighboring" threads. Obviously, it is necessary to organize in the program code a kind of time barrier, which each thread overcomes after all retain their intermediate results in the corresponding memory cells (step ( i )). Otherwise, some thread may go to stage ( ii ), while some other threads have not yet completed stage ( i ). Sadly, the creators of CUDA decided that such a special built-in synchronization mechanism for any number of threads on a single GPU is not needed. So how can you deal with this scourge? Although Google, judging by the prompts, is familiar with this issue, but it was not possible to find a ready-made satisfactory recipe for its task, but there are some pitfalls on the way to achieving the desired result for a beginner (which I am).
To begin with, let me on the basis of official documentation [1,2] and slides [3,4] , materials of various third-party sites [5-11] remind the general picture that a programmer faces when using CUDA. At the highest level of abstraction, he receives a parallel computing system with the SIMT ( Single-Instruction, Multiple-Thread ) architecture - one command is executed in parallel by many more or less independent threads . The combination of all these threads running under the same task (see Figure 1) is called the grid .
')

The parallel execution of the grid is ensured, first of all, by the presence on the video card of a greater number of identical scalar processors ( scalar processors ), which, in fact, run the threads (see Fig.3). Physically (see Fig. 2), scalar processors are part of streaming multiprocessors ( SM ).

For example, in my Tesla there are 30 SM, each with 8 scalar processors. However, on these 240 cores, it is possible to run grids from a much larger number of threads (1) thanks to the hardware mechanisms for the separation of available resources (both the working time of these cores and available memory). And some features of the implementation of just these mechanisms and determine the method of synchronization of threads when accessing a common memory for them.
One of such important features is the grouping of threads of 32 pieces per warp`s , which turn out to be parts of larger formations - blocks ( blocks ). All threads of each block (for example, for my Tesla block can contain a maximum of 512 threads (1) ) are started strictly on one SM, therefore they have access only to its resources. However, on one SM more than one block can be launched (see Figure 3), and resources will be divided equally between them.
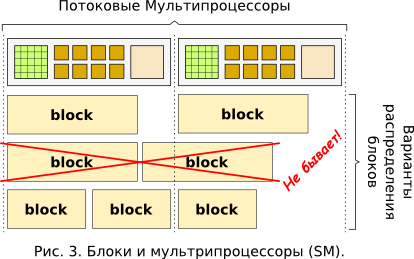
In each SM there is a control unit that distributes the CPU time resource. This is done in such a way that at each instant of time all the cores of one SM execute strictly one warp. And upon its completion, the next warp assigned to this SM is chosen in a clever, optimal way. Thus, it turns out that the streams of one warp are synchronized due to the hardware features of CUDA and are executed in an even closer to SIMD ( Single Instruction, Multiple Data ) method. But streams of even one block from different warps can turn out to be noticeably out of sync.
Another, no less important feature is the organization of memory in CUDA and the access of streams to its various parts. Global memory has the highest degree of general accessibility for streams, which is physically implemented in the form of integrated circuits sealed on a graphics card - the very same video memory, which is now calculated in gigabytes. The location outside the processor makes this type of memory the slowest compared to others provided for computing on a video card. Shared “shared access” has a shared memory (shared memory): located in each SM block (see Fig. 2), usually 16KB (1) in size, is available only to threads running on the cores of this SM (see Fig. 1, Fig.3). Since more than one block can be allocated to parallel execution on one SM, the entire amount of shared memory available in SM is divided equally between these blocks. It is necessary to mention that the shared memory is physically located somewhere very close to the SM cores, therefore it has a high access speed, comparable to the speed of the register ( registers ) - the main type of memory. Registers can serve as operands of elementary machine instructions, and are the fastest memory. All cash registers of one SM are equally divided between all threads running on this SM. The group of registers allocated for the use of any thread is available to him and only to him. As an illustration, the power of CUDA (or, on the contrary, the scale of a disaster): in the same Tesla, each SM leases 16,384 32-bit general purpose registers (1) .
From all the above, we can conclude that the interaction between the streams of one block should be attempted through their common fast shared memory, and between the streams of two different blocks - only using global memory. This is where the problem indicated in the introduction arises: monitoring the relevance of data in the public domain to different streams for reading and writing memory. In other words - the problem of synchronization of threads. As already noted, within one block, the flows of each warp are synchronized with each other. There are several barrier-type commands to synchronize block streams regardless of their belonging to warpas:
The first team sets a single barrier for all streams of one block, the other three - for each stream its own independent barrier. To synchronize the flow of the entire grid, you will need to come up with something else. Before considering this “more,” we specify the task so that we can give an example of a meaningful C code.
So, let's take a closer look at the following example. Let there be two areas in the adapter's global memory: under the arrays X [] and P [] with 128 elements each. Let the array X [] is written from the host (the central processor from the computer’s RAM). Create a grid of two blocks with 64 streams in each - that is, a total of 128 streams (see Figure 4).
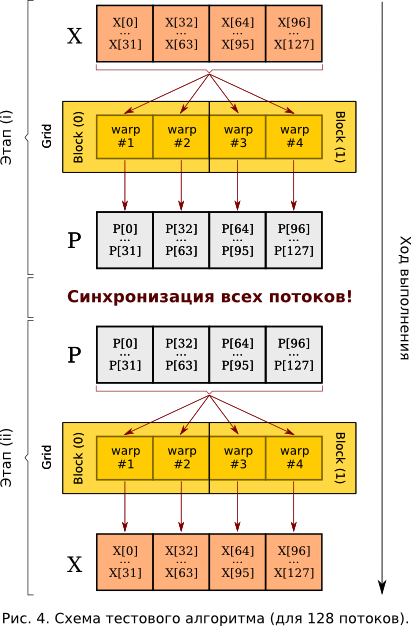
Now step ( i ) can be performed: each stream with number j will add together all the elements of the array X [], recording the result in P [j]. Next step ( ii ) must be performed: each j -th stream will begin to sum all the elements of the array P [], writing them into the corresponding X [j]. Of course, using CUDA for parallel execution of 128 times the same is meaningless, but in real life each flow will have its own set of weighting factors with which summation takes place, and the X transformation -> P and back, P -> X - occurs multiple times. In our example, we choose the coefficients equal to unity - for clarity and simplicity, which does not break the generality.
Let's move from theory to experiment. The algorithm is very transparent, and a person who has never dealt with multithreading can immediately suggest the following CUDA core code:
Repeated execution of this kernel will show that the P [] array will be the same from time to time, and, behold, X [] may sometimes differ. Moreover, if there is a difference, it will not be in one element of X [j], but in a group of consecutive 32 elements! In this case, the index of the first element in the erroneous block will also be a multiple of 32 - this is just a manifestation of synchronization in those same warpes and some dissynchronization of the streams of different warps. If the error occurred in some thread, then it will be in all the rest of his warp. If to apply the synchronization mechanism proposed by CUDA developers
then we will ensure that each flow of the block will produce the same result. And if somewhere it will be wrong - then the whole block. Thus, it remains to somehow synchronize different blocks.
Unfortunately, I know only two methods:
I did not like the first option very much, due to the fact that in my task such kernels should be called up often (thousands of times), and there is reason to fear the presence of additional delays on the very start of the kernel. At least, because at the beginning of each core, you need to prepare some variables, process the arguments of the kernel function ... It is more logical and faster to do this once in the “big” core, and then not to interfere with the CPU, leaving the graphics adapter to stew from the data in its own of memory.
As for the second option with the system of flags, a similar mechanism is mentioned in the section “B.5 Memory Fence Functions” in [1] . However, there is considered a slightly different algorithm for the kernel. To implement block synchronization, we introduce two functions: the first will prepare the values of the counter of the spent blocks, and the second will play the role of a barrier — delay each flow until all the blocks are completed. For example, these functions and the kernel using them may look like this:
That seems to be all. The flag was started, the functions were written. It remains to compare the performance of the first and second methods. But, unfortunately, the SyncWholeDevice () function will increment the counter, but the barrier delay will not provide. It would seem, why? There is a while loop . Here we just swim up to the underwater stone mentioned in the abstract, which becomes visible: if you look at the ptx file generated by the nvcc compiler [12-14] , it turns out that he kindly throws out an empty cycle from his point of view. Making the compiler not optimize the loop in this way can be done in at least two ways.
By all means working will be an explicit insert in ptx-assembler. For example, such a function, the call that should replace the while loop :
Another, syntactically more elegant way is to use the volatile specifier when declaring a counter flag. This will inform the compiler that a variable in global (or shared) memory can be changed by any thread at any time. Therefore, when accessing this variable, it is necessary to disable any optimization. The code will need to change only two lines:
We now give a rough theoretical estimate of the performance of the two methods of block synchronization. Rumor has it that a kernel call takes ~ 10µs - this is the cost of synchronization by repeatedly calling the cores. In the case of synchronization by introducing a barrier from a cycle, ~ 10 threads (depending on how many blocks) increment and read in a cycle one cell in the global memory, where each I / O operation takes about 500 cycles. Let each block conduct such operations. Then about 10 * 500 * 3 = 1.5 * 10 ^ 4 cycles will be spent on the synchronization operation. With a core frequency of 1.5 GHz, we get 1.0 * 10 ^ (- 5) sec = 10 μs. That is, the order of magnitudes is the same.
But, of course, it is curious to look at the results of at least some tests. In Figure 5, a post reader can see a comparison of the time spent on executing 100 consecutive conversions X -> P -> X , repeated 10 times for each configuration of the grid ʻa. A repetition of 10 times is done to average the time required for 100 transformations (2) .

In the horizontal plane, the number of blocks launched and the number of threads in each of them are plotted. On the vertical axis, the time gain in percent for the method “single kernel call, barriers inside” (we will call single kernel launch) relative to the multi kernel launch method is delayed. It is clearly seen that the gain on the grid configurations under consideration, although very small, is almost always positive. However, the more blocks become, the MKL method lags behind in performance. For 32 blocks, he even slightly beats the method of SQL. This is due to the fact that the more blocks, the more more threads (having threadIdx.x == 0 ) read the count variable from the slow global memory. And there is no mechanism “once read, gave meaning to all threads”. If we consider the change in relative performance depending on the number of threads in the block, with a constant number of blocks themselves, then we can also notice some regularity. But here, the effects unknown to the author related to the synchronization of threads in the block, the management of warpes in SM work here. Therefore, we refrain from further comments.
It is interesting to look at performance with an unchanged number of working threads (1024), but their different division into blocks. Figure 6 shows just the graphs of the renormalized time spent on 100 * 10 of the above transformations for the two methods (MKL and SKL).

In fact, this is a diagonal “cut” in Fig.5. It is clearly seen that at first, with larger blocks, the performance of both synchronization methods grows the same. About this effect, the developers of CUDA warn in the official documentation [2] , but the author, again, unfortunately, does not have the details of the mechanisms of this phenomenon. The reduction of the gap and even the loss of the method of SKL with the smallest division into blocks is connected, as already mentioned, with an increase in the number of readings of the variable count .
It should be noted that the tests were carried out with the implementation of the method SKL through the replacement of the while loop with a ptx-assembler insert. Using the volatile specifier sometimes (depending on the grid configuration) slows down the process and sometimes accelerates. The magnitude of the deceleration reaches 0.20%, and acceleration - 0.15%. This behavior, apparently, is determined by the peculiarities of the while loop implementation by the compiler and on the ptx-assembly insertion by humans, and allows us to consider both implementations of the SKL method to be equally productive.
In this article I have tried to highlight at the basic level the problem of synchronization of streams, methods of synchronizing blocks; after some tests, give a general description of the CUDA system with pictures. In addition, in the source code of the test program (2), the reader will be able to find another example of reliable buffer utilization in shared memory (threads are synchronized via __ syncthreads () ). I hope someone will be useful. For me personally, this information gathered in one place would save several days of experimenting with the code, and “googling”, since I have a stupid penchant for not very attentive reading the documentation.
(1) To obtain technical information about the adapters available in the computer, it is proposed to use the C-function CUDA API cudaGetDeviceProperties (...) [1-2, 15] .
(2) The source code of the test program, pasted on pastebin.com.
[1] CUDA C Programming Guide
[2] CUDA C Best Practices Guide
[3] Advanced CUDA Webinar: Memory Optimizations
[4] S. Tariq, An Introduction to GPU Computing and CUDA Architecture
[5] Vanderbilt University, ACCRE, GPU Computing with CUDA
[6] OmGTU, Radio Engineering Faculty, Department "Integrated Information Security", retraining program "Programming for graphics processors"
[7] Summer Supercomputer Academy, High-Performance Computing on Clusters Using NVIDIA Graphics Accelerators
[8] iXBT.com: NVIDIA CUDA - Non-graphical Computing on GPUs
[9] cgm.computergraphics.ru: Introduction to CUDA Technology
[10] THG.ru: nVidia CUDA: calculations on a video card or death of a CPU?
[11] steps3d.narod.ru: CUDA Basics, CUDA Programming (Part 2)
[12] The CUDA Compiler Driver (NVCC)
[13] Using Inline PTX Assembly in CUDA
[14] PTX: Parallel Thread Execution ISA Version 3.0
[15] CUDA API Reference Manual ( PDF , HTML online )
A few words about the CUDA architecture
To begin with, let me on the basis of official documentation [1,2] and slides [3,4] , materials of various third-party sites [5-11] remind the general picture that a programmer faces when using CUDA. At the highest level of abstraction, he receives a parallel computing system with the SIMT ( Single-Instruction, Multiple-Thread ) architecture - one command is executed in parallel by many more or less independent threads . The combination of all these threads running under the same task (see Figure 1) is called the grid .
')

The parallel execution of the grid is ensured, first of all, by the presence on the video card of a greater number of identical scalar processors ( scalar processors ), which, in fact, run the threads (see Fig.3). Physically (see Fig. 2), scalar processors are part of streaming multiprocessors ( SM ).

For example, in my Tesla there are 30 SM, each with 8 scalar processors. However, on these 240 cores, it is possible to run grids from a much larger number of threads (1) thanks to the hardware mechanisms for the separation of available resources (both the working time of these cores and available memory). And some features of the implementation of just these mechanisms and determine the method of synchronization of threads when accessing a common memory for them.
One of such important features is the grouping of threads of 32 pieces per warp`s , which turn out to be parts of larger formations - blocks ( blocks ). All threads of each block (for example, for my Tesla block can contain a maximum of 512 threads (1) ) are started strictly on one SM, therefore they have access only to its resources. However, on one SM more than one block can be launched (see Figure 3), and resources will be divided equally between them.

In each SM there is a control unit that distributes the CPU time resource. This is done in such a way that at each instant of time all the cores of one SM execute strictly one warp. And upon its completion, the next warp assigned to this SM is chosen in a clever, optimal way. Thus, it turns out that the streams of one warp are synchronized due to the hardware features of CUDA and are executed in an even closer to SIMD ( Single Instruction, Multiple Data ) method. But streams of even one block from different warps can turn out to be noticeably out of sync.
Another, no less important feature is the organization of memory in CUDA and the access of streams to its various parts. Global memory has the highest degree of general accessibility for streams, which is physically implemented in the form of integrated circuits sealed on a graphics card - the very same video memory, which is now calculated in gigabytes. The location outside the processor makes this type of memory the slowest compared to others provided for computing on a video card. Shared “shared access” has a shared memory (shared memory): located in each SM block (see Fig. 2), usually 16KB (1) in size, is available only to threads running on the cores of this SM (see Fig. 1, Fig.3). Since more than one block can be allocated to parallel execution on one SM, the entire amount of shared memory available in SM is divided equally between these blocks. It is necessary to mention that the shared memory is physically located somewhere very close to the SM cores, therefore it has a high access speed, comparable to the speed of the register ( registers ) - the main type of memory. Registers can serve as operands of elementary machine instructions, and are the fastest memory. All cash registers of one SM are equally divided between all threads running on this SM. The group of registers allocated for the use of any thread is available to him and only to him. As an illustration, the power of CUDA (or, on the contrary, the scale of a disaster): in the same Tesla, each SM leases 16,384 32-bit general purpose registers (1) .
From all the above, we can conclude that the interaction between the streams of one block should be attempted through their common fast shared memory, and between the streams of two different blocks - only using global memory. This is where the problem indicated in the introduction arises: monitoring the relevance of data in the public domain to different streams for reading and writing memory. In other words - the problem of synchronization of threads. As already noted, within one block, the flows of each warp are synchronized with each other. There are several barrier-type commands to synchronize block streams regardless of their belonging to warpas:
- __syncthreads () is the surest way. This function will cause each thread to wait until (a) all other threads of this block reach this point and (b) all operations on access to shared and global memory completed by the threads of this block are completed and become visible to the threads of this block . You do not need to place this command inside the conditional if statement , but you should ensure that the unconditional call to this function is performed by all threads of the block.
- __threadfence_block () will keep waiting for the thread that caused it until all committed access operations to the shared and global memory are completed and are visible to the threads of this block .
- __threadfence () will make the thread that caused it wait until all committed access operations to shared memory become visible to the threads of this block , and global memory operations to all threads on the “device” . The term "device" means a graphic adapter.
- __threadfence_system () is similar to __threadfence () , but turns on synchronization with threads on the CPU ("host"), using a very convenient page-locked memory. Read more in [1,2] and some other sources listed in the list below.
The first team sets a single barrier for all streams of one block, the other three - for each stream its own independent barrier. To synchronize the flow of the entire grid, you will need to come up with something else. Before considering this “more,” we specify the task so that we can give an example of a meaningful C code.
Task details
So, let's take a closer look at the following example. Let there be two areas in the adapter's global memory: under the arrays X [] and P [] with 128 elements each. Let the array X [] is written from the host (the central processor from the computer’s RAM). Create a grid of two blocks with 64 streams in each - that is, a total of 128 streams (see Figure 4).

Now step ( i ) can be performed: each stream with number j will add together all the elements of the array X [], recording the result in P [j]. Next step ( ii ) must be performed: each j -th stream will begin to sum all the elements of the array P [], writing them into the corresponding X [j]. Of course, using CUDA for parallel execution of 128 times the same is meaningless, but in real life each flow will have its own set of weighting factors with which summation takes place, and the X transformation -> P and back, P -> X - occurs multiple times. In our example, we choose the coefficients equal to unity - for clarity and simplicity, which does not break the generality.
Let's move from theory to experiment. The algorithm is very transparent, and a person who has never dealt with multithreading can immediately suggest the following CUDA core code:
__global__ void Kernel(float *X, float *P) { const int N = 128; // . const int index = threadIdx.x + blockIdx.x*blockDim.x; // . float a; // . . /* (i): */ a = X[0]; for(int j = 1; j < N; ++j) // , a += X[j]; P[index] = a / N; // , . /* (i). */ /* (ii): */ a = P[0]; for(int j = 1; j < N; ++j) // , a += P[j]; X[index] = a / N; // , . /* (ii). */ } Repeated execution of this kernel will show that the P [] array will be the same from time to time, and, behold, X [] may sometimes differ. Moreover, if there is a difference, it will not be in one element of X [j], but in a group of consecutive 32 elements! In this case, the index of the first element in the erroneous block will also be a multiple of 32 - this is just a manifestation of synchronization in those same warpes and some dissynchronization of the streams of different warps. If the error occurred in some thread, then it will be in all the rest of his warp. If to apply the synchronization mechanism proposed by CUDA developers
__global__ void Kernel(float *X, float *P) { ... /* (i). */ __syncthreads(); /* (ii): */ ... } then we will ensure that each flow of the block will produce the same result. And if somewhere it will be wrong - then the whole block. Thus, it remains to somehow synchronize different blocks.
Solution methods
Unfortunately, I know only two methods:
- The CUDA core terminates if and only if all threads terminate. Thus, one core can be broken into two and called from the main program sequentially;
- Come up with a system of flags in the global memory.
I did not like the first option very much, due to the fact that in my task such kernels should be called up often (thousands of times), and there is reason to fear the presence of additional delays on the very start of the kernel. At least, because at the beginning of each core, you need to prepare some variables, process the arguments of the kernel function ... It is more logical and faster to do this once in the “big” core, and then not to interfere with the CPU, leaving the graphics adapter to stew from the data in its own of memory.
As for the second option with the system of flags, a similar mechanism is mentioned in the section “B.5 Memory Fence Functions” in [1] . However, there is considered a slightly different algorithm for the kernel. To implement block synchronization, we introduce two functions: the first will prepare the values of the counter of the spent blocks, and the second will play the role of a barrier — delay each flow until all the blocks are completed. For example, these functions and the kernel using them may look like this:
__device__ unsigned int count; // - . //4 . /* -: */ __device__ void InitSyncWholeDevice(const int index) { if (index == 0) // grid` ( 0) count = 0; // . if (threadIdx.x == 0) // block` , - while (count != 0); // . // block` , : __syncthreads(); // , - . device - . } /* device: */ __device__ void SyncWholeDevice() { // : unsigned int oldc; // , gmem smem, grid`: __threadfence(); // block` ( ) //-: if (threadIdx.x == 0) { // oldc count "+1": oldc = atomicInc(&count, gridDim.x-1); // , "" gmem: __threadfence(); // ( count ), // count, , // gmem. , "", //, "" . if (oldc != (gridDim.x-1)) while (count != 0); } // , : __syncthreads(); } __global__ void Kernel_Synced(float *X, float *P) { InitSyncWholeDevice(threadIdx.x + blockIdx.x*blockDim.x); ... /* (i). */ SyncWholeDevice(); /* (ii): */ ... } That seems to be all. The flag was started, the functions were written. It remains to compare the performance of the first and second methods. But, unfortunately, the SyncWholeDevice () function will increment the counter, but the barrier delay will not provide. It would seem, why? There is a while loop . Here we just swim up to the underwater stone mentioned in the abstract, which becomes visible: if you look at the ptx file generated by the nvcc compiler [12-14] , it turns out that he kindly throws out an empty cycle from his point of view. Making the compiler not optimize the loop in this way can be done in at least two ways.
By all means working will be an explicit insert in ptx-assembler. For example, such a function, the call that should replace the while loop :
__device__ void do_while_count_not_eq(int val) { asm("{\n\t" "$my_while_label: \n\t" " .reg .u32 r_count; \n\t" " .reg .pred p; \n\t" " ld.global.u32 r_count, [count]; \n\t" " setp.ne.u32 p, r_count, %0; \n\t" "@p bra $my_while_label; \n\t" "}\n\t" : : "r"(val)); } Another, syntactically more elegant way is to use the volatile specifier when declaring a counter flag. This will inform the compiler that a variable in global (or shared) memory can be changed by any thread at any time. Therefore, when accessing this variable, it is necessary to disable any optimization. The code will need to change only two lines:
__device__ volatile unsigned int count; // - . //4 . ... // oldc count "+1": oldc = atomicInc((unsigned int*)&count, gridDim.x-1); ... Evaluation of solution methods
We now give a rough theoretical estimate of the performance of the two methods of block synchronization. Rumor has it that a kernel call takes ~ 10µs - this is the cost of synchronization by repeatedly calling the cores. In the case of synchronization by introducing a barrier from a cycle, ~ 10 threads (depending on how many blocks) increment and read in a cycle one cell in the global memory, where each I / O operation takes about 500 cycles. Let each block conduct such operations. Then about 10 * 500 * 3 = 1.5 * 10 ^ 4 cycles will be spent on the synchronization operation. With a core frequency of 1.5 GHz, we get 1.0 * 10 ^ (- 5) sec = 10 μs. That is, the order of magnitudes is the same.
But, of course, it is curious to look at the results of at least some tests. In Figure 5, a post reader can see a comparison of the time spent on executing 100 consecutive conversions X -> P -> X , repeated 10 times for each configuration of the grid ʻa. A repetition of 10 times is done to average the time required for 100 transformations (2) .

In the horizontal plane, the number of blocks launched and the number of threads in each of them are plotted. On the vertical axis, the time gain in percent for the method “single kernel call, barriers inside” (we will call single kernel launch) relative to the multi kernel launch method is delayed. It is clearly seen that the gain on the grid configurations under consideration, although very small, is almost always positive. However, the more blocks become, the MKL method lags behind in performance. For 32 blocks, he even slightly beats the method of SQL. This is due to the fact that the more blocks, the more more threads (having threadIdx.x == 0 ) read the count variable from the slow global memory. And there is no mechanism “once read, gave meaning to all threads”. If we consider the change in relative performance depending on the number of threads in the block, with a constant number of blocks themselves, then we can also notice some regularity. But here, the effects unknown to the author related to the synchronization of threads in the block, the management of warpes in SM work here. Therefore, we refrain from further comments.
It is interesting to look at performance with an unchanged number of working threads (1024), but their different division into blocks. Figure 6 shows just the graphs of the renormalized time spent on 100 * 10 of the above transformations for the two methods (MKL and SKL).

In fact, this is a diagonal “cut” in Fig.5. It is clearly seen that at first, with larger blocks, the performance of both synchronization methods grows the same. About this effect, the developers of CUDA warn in the official documentation [2] , but the author, again, unfortunately, does not have the details of the mechanisms of this phenomenon. The reduction of the gap and even the loss of the method of SKL with the smallest division into blocks is connected, as already mentioned, with an increase in the number of readings of the variable count .
It should be noted that the tests were carried out with the implementation of the method SKL through the replacement of the while loop with a ptx-assembler insert. Using the volatile specifier sometimes (depending on the grid configuration) slows down the process and sometimes accelerates. The magnitude of the deceleration reaches 0.20%, and acceleration - 0.15%. This behavior, apparently, is determined by the peculiarities of the while loop implementation by the compiler and on the ptx-assembly insertion by humans, and allows us to consider both implementations of the SKL method to be equally productive.
Conclusion
In this article I have tried to highlight at the basic level the problem of synchronization of streams, methods of synchronizing blocks; after some tests, give a general description of the CUDA system with pictures. In addition, in the source code of the test program (2), the reader will be able to find another example of reliable buffer utilization in shared memory (threads are synchronized via __ syncthreads () ). I hope someone will be useful. For me personally, this information gathered in one place would save several days of experimenting with the code, and “googling”, since I have a stupid penchant for not very attentive reading the documentation.
(1) To obtain technical information about the adapters available in the computer, it is proposed to use the C-function CUDA API cudaGetDeviceProperties (...) [1-2, 15] .
(2) The source code of the test program, pasted on pastebin.com.
List of information sources
[1] CUDA C Programming Guide
[2] CUDA C Best Practices Guide
[3] Advanced CUDA Webinar: Memory Optimizations
[4] S. Tariq, An Introduction to GPU Computing and CUDA Architecture
[5] Vanderbilt University, ACCRE, GPU Computing with CUDA
[6] OmGTU, Radio Engineering Faculty, Department "Integrated Information Security", retraining program "Programming for graphics processors"
[7] Summer Supercomputer Academy, High-Performance Computing on Clusters Using NVIDIA Graphics Accelerators
[8] iXBT.com: NVIDIA CUDA - Non-graphical Computing on GPUs
[9] cgm.computergraphics.ru: Introduction to CUDA Technology
[10] THG.ru: nVidia CUDA: calculations on a video card or death of a CPU?
[11] steps3d.narod.ru: CUDA Basics, CUDA Programming (Part 2)
[12] The CUDA Compiler Driver (NVCC)
[13] Using Inline PTX Assembly in CUDA
[14] PTX: Parallel Thread Execution ISA Version 3.0
[15] CUDA API Reference Manual ( PDF , HTML online )
Source: https://habr.com/ru/post/151897/
All Articles