Russian Code Cup 2012: a detailed analysis of the tasks from the final in pictures, video and examples
 On September 10, 2012, the Russian Code Cup 2012 Programming Championship was completed. A detailed account of how everything happened was published earlier , and today we will examine the tasks that have been proposed to the finalists. There were only six of them, and each of them is a separate interesting story:
On September 10, 2012, the Russian Code Cup 2012 Programming Championship was completed. A detailed account of how everything happened was published earlier , and today we will examine the tasks that have been proposed to the finalists. There were only six of them, and each of them is a separate interesting story:- about evil birds running along the branch
- about the inhabitants of the planet Trisol - Trisolians - with their cunning system of keeping life histories,
- about the fabulous city of Aldersberg , where our finalists are waiting for a decision (citizens need to arrange their magical artifacts in order to survive the siege of enemies),
- about the hard life of a dual-core processor ,
- and also about the machine mixing the pack of cards
- and about finding the length of the race track .
Three hours were allocated for solving these problems. The only one who solved five problems out of six was the winner of the Russian Code Cup 2012 Vladislav Epifanov . Slightly less than half of the finalists decided on four tasks. The first three tasks did almost everything. The task about the deck of cards was solved correctly only by one Eugene Kapun . The second place in the tournament was taken by Natalya Bondarenko , who solved four tasks faster than others and with a smaller number of attempts.
')
Angry Birds
Andrei KALININ , the head of the Mail.Ru Search developers department , will tell about the problem statement.
The task is called "Angry Birds." Its essence is simple. There is a wire of finite length on which the birds are located. Some birds go to the right, some to the left. When they meet each other, they change direction. When they reach the end of the wire, they take off. We need to determine when each of these birds will take off. According to the conditions of the problem there may be up to 100,000 birds marching in each direction, therefore, in total there are not more than 200,000.

Detailed statement of the problem
As you know, birds love to sit on the wires. In the county town of K there is one long, especially favorite wire. At one point, there were several birds perched on it. Everything would be fine, but here only a pig running under the wire raised such a cloud of dust that it made the birds very angry.
Becoming evil, the birds began to run on this wire in different directions - someone to the left, someone to the right. In this case, all the birds began to run at the same speed, equal to one meter per minute. When two birds meet, moving towards each other, they immediately turn around and begin to run at the same speed in the opposite direction.
This process would continue indefinitely, but only the wire was nevertheless finite, and as soon as one of the birds reaches the end of the wire, it immediately takes off, and all the other birds, stunned by this, turn around and begin to run in the opposite direction. If two birds reach the edge at the same time, then two reversals take place, or, which is the same, nothing happens.
You need to write a program that, according to the length of the wire, the initial positions and directions of the birds running, will find out for each bird at what point in time it will fly away from the wire.
Input Format
The first line contains a single integer L (1 ≤ L ≤ 109) - the length of the wire in meters.
The second line contains the number n (0 ≤ n ≤ 100 000) - the number of birds running to the right. The third line contains n different integers a i (0 <a i <L) - the distance in meters from the left end of the wire to the birds running to the right.
The fourth line contains the number m (0 ≤ m ≤ 100 000) - the number of birds running to the left. The fifth line contains m different integers b i (0 <b i <L) - the distance in meters from the left end of the wire to the birds running to the left.
No two birds are originally in the same place. It is guaranteed that at least one bird is sitting on the wire.
Output format
In the first line print n integers t i - in how many minutes the ith bird will fly away in the order of description in the input, running to the right. In the second line print m integers u i - in how many minutes the ith bird will fly away in the order of description in the input, running to the left.
Time limit - 2 seconds
Memory limit - 256 megabytes
An example was given in the problem. To explain its statement and decision, it will be useful to track the movement of the birds every minute using this example. It provides the following introductory data: two birds are on the 8th and 9th meter and go to the right, three more birds are on the 2nd, 5th and 7th meter and go to the left. The length of the wire is 10 meters. This is the initial situation. It is necessary to calculate when a bird takes off.
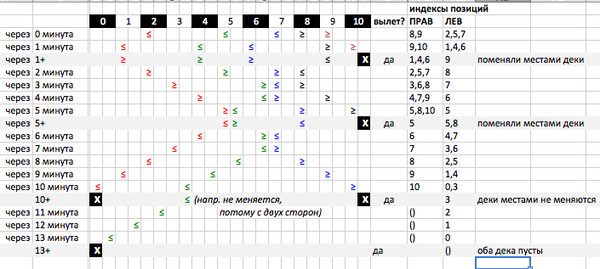
As can be seen, in the first and fifth minutes the birds fly away from the right end, on the tenth two birds fly at once, and on the thirteenth the last flies.
It is important to note here that the order of the birds never changes. Also note that, despite the zigzags described by birds, the number of birds moving left or right does not depend on their collision, and the nature of the change in motion coordinates always remains linear. This is clearly visible in the interval from the first to the fifth minute, when there were already three collisions.
On the right in two columns I indicated the position of the birds. Immediately it becomes obvious that the moment of the first take-off from the wire can be predicted - the number of minutes (= number of meters) to the end of the wire from the nearest to one of the ends of the bird.
It also shows that after takeoff, all coordinates attached to the movement to the right become coordinates attached to the movement to the left, and vice versa.
As a result, the solution of the problem is reduced to the management of two decks (deque) - data structures of the type “double-ended queue”, in which the removal of the first or last element is carried out in O (1). When the bird takes off, the extreme element is removed from the deck, and the decks themselves change places. Storing couples <dec; how many it is necessary to add to the numbers in it> it is possible for O (1) to find, after what time and in which direction the next bird will fly. Since the order of the birds does not change, a sorted array of coordinates of the original location of the birds should also be stored in order to determine which bird left the wire.
The most beautiful solution is the solution on Python3:
from collections import deque length = int(input()) n = int(input()) right = deque(sorted(map(int, input().split()))) m = int(input()) left = deque(sorted(map(int, input().split()))) addLeft, addRight = 0, 0 INF = 2*10**9 ans = 0 while right or left: L = left[0] + addLeft if left else INF R = length - (right[-1] + addRight) if right else INF m = min(L, R) ans += m addLeft -= m addRight += m if L < R: left.popleft() left, addLeft, right, addRight = right, addRight, left, addLeft elif L == R: left.popleft() right.pop() else: right.pop() left, addLeft, right, addRight = right, addRight, left, addLeft print (ans) The task with the birds was first done by Michael KEVER by the 22nd minute since the start of the round. A few seconds later, the task was handed over to Vasil Biletsky .
In total, 40 people coped with the task, and 11 people started solving it. The average time to solve it is 30 minutes. Of these, the biggest time to resolve is 44 minutes (not counting situations where no decision was sent at all). All 11 people who successfully solved the first task of the first, decided at least two more. With the exception of 2 cases out of 11, they all went to task B, and then to task C, that is, they performed tasks in alphabetical order. This task is in third place among all the tasks from which the contest began.
Trisolians
Ilya WAISMAN , technical director of Allods Online, tells us about the Trisolians problem:
According to the condition of the problem, some inhabitants of the planet Trisol designate their age not as a single integer, as we, earthlings, but with a vector of k integers. In a newborn Trisolian, the age vector consists of only zeros, but every year an adult grows, each positive element of each element of the age vector is added. The life history of a Trisolian is a collection of all the age vectors that he had during his life. It is precisely known that Trisolians with the same history do not exist. Scientists are interested in what the maximum number of Trisolians life history ends on a vector, the sum of the elements of which is equal to n. You need to write a program that calculates this value modulo a prime number 7340033 = 7 * 2 ^ 20 + 1.
For example, for k = 2 there can exist 8 Trisolians, whose life history ends on a vector with the sum of 5.
1. (0, 0) - (1, 1) - (2, 3);
2. (0, 0) - (1, 1) - (3, 2);
3. (0, 0) - (1, 2) - (2, 3);
4. (0, 0) - (1, 4);
5. (0, 0) - (2, 1) - (3, 2);
6. (0, 0) - (2, 3);
7. (0, 0) - (3, 2);
8. (0, 0) - (4, 1).
Detailed statement of the problem
Recently it became known that the inhabitants of the planet Trisol designate their age not as a single integer, as we are earthlings, but as a vector of k integers. It is believed that in a newborn Trisolian the vector of its age consists of k zeros. As they grow older, each year, to each element of the age vector, some positive number is added.
The life history of a Trisolian is the set of all vectors of his age that he had during his life. Earth scientists have found that there are no two Trisolians with the same history.
Now scientists are interested in what is the maximum number of Trisolians, the life story ends on a vector whose sum of elements is equal to n. Write a program that calculates this value modulo a prime number 7340033 = 7 · 220 + 1.
Input Format
The first line contains two integers n and k - the sum of the elements of the last vector of age, and the number of elements in the vector (1 ≤ n ≤ 4239, 1 ≤ k ≤ 10 9 ).
Output format
Print the maximum number of Trisolians whose life history can end on a vector whose sum of elements is equal to n. The answer should be displayed modulo 7340033 = 7 · 2 20 + 1.
 A little historical background, without which the solution of the problem is probably impossible. The Trisolians are the inhabitants of the planet Trisol, located deep within the Forbidden Zone in the Galaxy of Terror. Consist of 100% liquid. Can easily change their shape. Ordinary people are peaceful, which is not the ruling elite. From time to time they drink each other, moving in this way along the career ladder.
A little historical background, without which the solution of the problem is probably impossible. The Trisolians are the inhabitants of the planet Trisol, located deep within the Forbidden Zone in the Galaxy of Terror. Consist of 100% liquid. Can easily change their shape. Ordinary people are peaceful, which is not the ruling elite. From time to time they drink each other, moving in this way along the career ladder.The task is relatively simple, because all its solution is reduced to combinatorics. On the other hand, it immediately becomes not as simple as it seems when you look at the possible range of k - vector dimensions (1 ≤ k ≤ 10000000000).
| N = 2 | N = 3 | N = 4 | N = 5 | N = 6 |
| (0,0) - (1,1) | (0,0) - (1,2) (0,0) - (2,1) | (0,0) - (1,1) - (2,2) (0,0) - (2,2) (0,0) - (3,1) (0,0) - (1,3) | (0, 0) - (1, 1) - (2, 3); (0, 0) - (1, 1) - (3, 2); (0, 0) - (1, 2) - (2, 3); (0, 0) - (2, 1) - (3, 2); (0, 0) - (2, 3); (0, 0) - (3, 2); (0, 0) - (4, 1). (0, 0) - (1, 4); | (0,0) - (1,1) - (2,2) - (3,3) (0,0) - (1,1) - (4,2) (0,0) - (1,1) - (2,4) (0,0) - (1,1) - (3,3) (0,0) - (1,2) - (3,3) (0,0) - (1,2) - (2,4) (0,0) - (2,1) - (3,3) (0,0) - (2,1) - (4,2) (0,0) - (2,2) - (3,3) (0,0) - (3,1) - (4,2) (0,0) - (1,3) - (2,4) (0,0) - (5,1) (0,0) - (1,5) (0,0) - (4,2) (0,0) - (2,4) (0,0) - (3,3) |
| 1 option | 2 options | 4 options | 8 options | 16 options |
The key idea to understand the solution is that the “bushes” for large values of N partially consist of solutions for smaller values, which allows you to organize calculations through recursion.
Graphically, for the particular case of k = 2, the life history can be displayed as a set of segments connecting the zero mark with positive integer marks lying on the axis on the line f (x) = nx.
Here is the solution for N = 4:
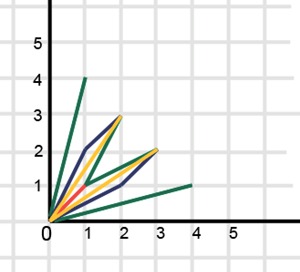
For N = 4 stories - eight.
Now add the vector (1,1) to this story and get
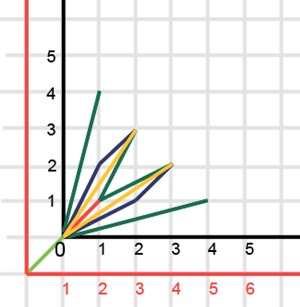
Each of the stories beginning with the vector (1,1) will be part of the history for N = 7. The other part of the story will be smaller bushes, starting with the vector (1,2), etc.
Similar story with other vectors. Let us give an example for the vector (1,3), which is the beginning of a part of the elements of history for N = 7. In this case, the following will be released:
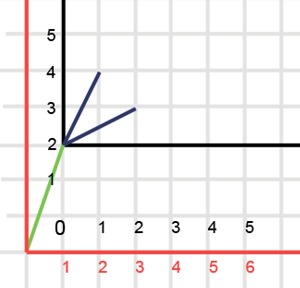
That is, if we take the vector that was given to the Trisolian for the first year of birth, and subtract it from all vectors of the life history of the Trisolian, then after discarding this vector we will actually get some life history of the Trisolian, whose sum of the elements of the last vector is n - (the sum elements of the ejected vector).
Thus, it can be understood that all stories in which the sum of the elements of the last vector is equal to n can be obtained from stories with the last vector having the sum of elements m for some m <n, adding some vector of positive elements with a sum equal to n - m co the whole history of life.
How many such vectors will be with a sum equal to nm? The minimum vector includes one in each coordinate, hence the total of vectors, of the entire component k, as a result, the sum nmk appears. It is necessary now to distribute units to k coordinates. The number of ways to do this is the number of combinations with repetitions. The number of combinations with repetitions is calculated as
And the number of combinations without repetitions is calculated as
From which it is easily deduced that the number of combinations with repetitions of a in b is equal to the number of combinations without repetitions of a + b - 1 in b.
So in our case the number of ways is C out of n - m - k + k - 1 by
k, i.e. C from n - m - 1 through k.
Denoting the desired value as ans n , we get the following recurrent formula :. It is assumed that ans 0 = 1. The running time of the algorithm is O (n2).
where C (x, y) is the number of combinations of the second argument in the first, calculated as x! / (xy)! / y!
The task of the Trisolians was done by almost all of those present at the final (except for two people). It took about 18 minutes to complete the task. The first was made by Roman RIZVANOV at the 11th minute, with a small margin - Yevgeny KAPUN .
CPU
Alexander GORNY , CIO Mail.Ru Group will tell about the processor problem:
The task involves a dual-core processor that can perform 26 different instructions. Each instruction is symbolically written with the letter of the English alphabet. Programs consist of a set of instructions. It is necessary to calculate what minimum time the processor will need to process the specified 2n programs (which in turn consist of specific instructions consisting of the specified sequence), if it is known that due to the architecture in the two cores, only identical instructions can be executed at one time, and n - the number of such processors.
Illustration of how a processor can process two programs at the same time:
The task comes down to how to efficiently scatter 2n programs across n processors and two cores in each so that the number of steps is minimal.
Detailed statement of the problem
As is known, most of the processors currently being manufactured are multi-core, that is, they support the execution of several instructions simultaneously. Paraltel has developed a new type of dual-core processor that allows you to perform 26 different instructions, denoted by capital Latin letters. Execution of each such instruction requires exactly one processor cycle.
The program for this processor is a sequence of instructions. The instructions of the program must be executed in the order in which they follow in the program; it is not allowed to interchange instructions.
Due to the presence of two cores, the processor can simultaneously execute two programs - one on each core. However, due to the nature of the architecture, only identical instructions can be executed simultaneously on two cores of the same processor.
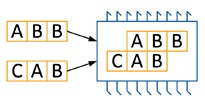
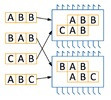
When two programs are executed on a processor, a special control device optimizes execution so as to complete the execution of both programs as early as possible. For example, the programs “ABB” and “ABC” can be executed on the processor in 4 cycles: first, the commands “A” of both programs are executed simultaneously on different cores, then the commands “B” simultaneously, then the command “B” from the first program and, finally, "C" of the second. Similarly, the programs "CAB" and "BAB" are executed in 4 cycles.
Recently, company specialists have assembled a supercomputer from n processors, on which it is necessary to run 2n programs. The organization of calculations is such that each processor must execute exactly two programs from this set, one on each core.
You need to plan the execution of 2n programs on n processors so that the completion time of all programs is minimal.
Input Format
The first line contains the number n (1 ≤ n ≤ 10) - the number of processors. Further, in 2n lines, the programs that must be executed are specified. Each program contains from 1 to 100 teams. Each command is given a capital Latin letter.
Output format
Print a single number - the minimum time for which you can run all the programs.
As an example, the task is a set of the following programs: ABB BAB CAB ABC
and information that there are two processors.
These four steps are needed to run the program on two processors:
| Processor 1 core 1 | Processor 1 core 2 | Processor 2 core 1 | Processor 2 core 2 |
| [A] BB | [A] BC | [B] AB | |
| A [B] B | A [B] C | [C] AB | |
| AB [B] | B [A] B | C [A] B | |
| AB [C] | BA [B] | CA [B] |
We divide the solution of the problem into two stages and consider each separately.
The first step will be the construction of the graph. The vertices of it are 2n programs that we need to execute. The graph will be weighted, and the weight of the edge between the two programs is equal to the amount of time the processor will spend on their joint execution. This value is equal to the sum of program lengths minus those commands that will be executed simultaneously. And there are no more such commands than LCS (a, b), where a and b are the lines describing the programs, and LCS ( Longest Common Subsequence , the greatest common subsequence) is the function that finds the greatest common subsequence of the two sequences.
As a result, the function of finding the weight of the edge will look like this:
int dist(String a, String b) { int[][] d = new int[a.length() + 1][b.length() + 1]; for (int[] ar : d) { Arrays.fill(ar, 1000000000); } d[0][0] = 0; for (int i = 0; i <= a.length(); ++i) { for (int j = 0; j <= b.length(); ++j) { if (i < a.length()) { d[i + 1][j] = Math.min(d[i + 1][j], d[i][j] + 1); } if (j < b.length()) { d[i][j + 1] = Math.min(d[i][j + 1], d[i][j] + 1); } if (i < a.length() && j < b.length() && a.charAt(i) == b.charAt(j)) { d[i + 1][j + 1] = Math.min(d[i + 1][j + 1], d[i][j] + 1); } } } return d[a.length()][b.length()]; } The second stage of the solution will be finding a perfect matching in this graph, in which the weight of the maximum edge is minimized. One of the simplest algorithms that solve this problem and fit into the time constraints is dynamic programming, but by subsets. Suppose that for each set of vertices of size at most k, we know the answer. In this case, sorting through all such sets and adding to each one all possible edges that are not yet in it, we will be able to calculate the answer for all sets of size no more than k + 2.
int[] d = new int[1 << (2 * n)]; Arrays.fill(d, 1000000000); d[0] = 0; for (int mask = 0; mask + 1 < 1 << (2 * n); ++mask) { if (d[mask] == 1000000000) { continue; } int i = 0; while ((mask & (1 << i)) != 0) { ++i; } for (int j = i + 1; j < 2 * n; ++j) { if ((mask & (1 << j)) == 0) { d[mask | (1 << i) | (1 << j)] = Math.min(d[mask | (1 << i) | (1 << j)], Math.max(d[mask], dist[i][j])); } } } Task "Processor" did almost all of those present at the finals (except for two people). The average time to solve this problem is about 18 minutes. The first to solve the problem was Vladislav EPIFANOV in the 11th minute.
Siege
Pavel KROTKOV , a student at the Department of ITMO, will tell you about the “Siege” task.
The task tells about the fantastic city of Aldersberg, which is about to come hordes of enemies. In order to keep the city, you need to put a barrier of n artifacts, and activate each i-th artifact with magical energy in the amount of a [i] merlin. After that, using b [i] merlin, the enemy will be able to destroy this artifact from a distance. Defenders of the city have A merlin of magical energy, in the arsenal of the enemy - B merlin. The townspeople decided to activate the artifacts so that after their destruction by the enemy magicians, the maximum number of artifacts remains active. You need to help the defenders of the city to choose which artifacts to activate.
Detailed statement of the problem
For the glorious city of Aldersberg hard times have come. From minute to minute, countless hordes of enemies will go on assault. Only magical barriers can help keep the city.
In the arsenal of the defenders of the city there are n artifacts that allow you to put a barrier. To activate the i-th artifact requires a i merlin (units of magical energy). After that, using b i merlin, the enemy can destroy the artifact at a distance.
The defenders of the city have A merlin of magical energy, in the arsenal of the enemy B merlin. Stocks of magical energy are not replenished. The townspeople decided to activate the artifacts so that after their destruction by the enemy’s mages, the maximum number remains active.
Help the city defenders choose which artifacts to activate.
Input Format
The first line contains three integers A, B and n (0 ≤ A, B ≤ 105, 0 ≤ n ≤ 1000), separated by spaces. The next n lines contain pairs of numbers ai and bi (1 ≤ a i , b i ≤ 105).
Output format
In the first line print the number of artifacts that will remain active under optimal actions of both parties to the conflict. In the second line print the number of artifacts, which should be activated by the defenders of the city, and the numbers of these artifacts. Separate the numbers in one line with spaces.
The artifacts are numbered, starting from one, in the order in which they are given in the input.
 A little historical background. Aldersberg is the second largest city in one of the four Northern Kingdoms, Aedirne, located on the very edge of the world. The town of Aldersberg was built around the walls of the fortress that guarded the borders of Aedirna ( Andrzej Sapkowski )
A little historical background. Aldersberg is the second largest city in one of the four Northern Kingdoms, Aedirne, located on the very edge of the world. The town of Aldersberg was built around the walls of the fortress that guarded the borders of Aedirna ( Andrzej Sapkowski )Suppose the defenders of the city activated some artifacts. The optimal strategy for their enemies will be to destroy them in the order of increasing b i . Indeed, the goal of the enemy is to destroy as many artifacts as possible. It makes no sense to spend a lot of energy on a hard-to-destroy artifact, as long as there is an easy target.
Renumber the artifacts in the non-decreasing order b i . Let it be known that the first artifact, which the enemy cannot destroy at the optimal actions of the defenders, has the number k. We describe the actions of the defenders, based on this assumption. It is necessary to select several of the first k − 1 artifacts so that the total energy expended to destroy them is at least B – b k +1 merlines, and the activation energy is minimal. Activate the k-th artifact. Finally, the last n − k artifacts are activated in order of increasing energy costs.
Unfortunately, k is not known in advance. We will go through the number of the first artifact that the enemy cannot destroy, and build the optimal answer for this assumption.
Let D ij be the minimum energy required to activate artifacts with numbers no more than i (up to 1000), such that their destruction will require j merlin of magical energy (up to 100,000). Transition: D i, j = min (D i − 1 , j, D i − 1 , j − b i + a i ). These two cases correspond to whether it is necessary to activate the artifact number i in order to achieve the optimal D ij .
In the array D we find the energy necessary for the fact that the enemy could not destroy the k-th artifact. After that, we greedily take the rest, while there is enough energy for activation. In the end, going through all the k we find the optimal answer.
The working time of the described approach is O (n (B + n)). In order to turn it into a full-fledged solution, you need to add information storage to restore the answer, which does not affect the asymptotics.
The memory bottleneck could become a bottleneck. Note that the array D can only store the last line. In addition, for each pair (i, j), it is enough to know whether it is necessary to activate the artifact number i in order to achieve the optimal D ij . In order to meet the memory constraints, it was necessary to use no more than two bytes to store this bit of information.
The task “Siege” was solved by 19 people. Peter MITRICHEV coped with this task the fastest in the 87th minute (Peter successfully passed the first three tasks before the Siege task).
Deck shuffle
Sergey Melnikov , a student at NRU ITMO, tells about the problem of mixing the deck:
In this task, you need to think about the deck mixing mechanism, which allows you to mix it ideally (that is, to make no two identical cards follow each other) for the minimum number of card block movements from the middle to the end of the deck. . Initially, the deck is sorted by non-decreasing dignity. Given the number of different advantages of cards, the order of cards in the deck, the number of decks.
Detailed statement of the problem
Automation and computerization are rapidly entering into all spheres of our life. Dishwashers, on-board computers in cars, electric fly swatches — all these devices in one degree or another make standard habitual actions easier for a person. In the same task, you will be required to automate another familiar to many action - mixing a deck of cards.
, , 1 t. , .
. , 1, — t. , , .
, .
, : i j , i- j- .
, , .
Input Format
x — , . x .
. n — . n , . , , 1.
200000.
Output format
, , «-1», , , . , k — , . k , i j — , , .
, , :
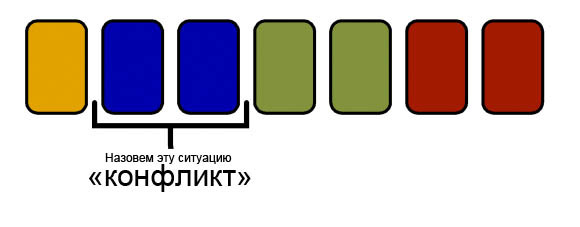
, , . , .
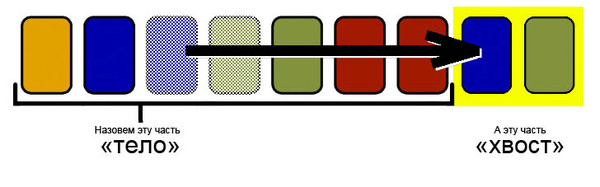
. , . , .
K. , ⌈K / 2⌉ ( ⌊…⌋ ⌈…⌉ — ).
M «». , M = ⌈K / 2⌉.
, .
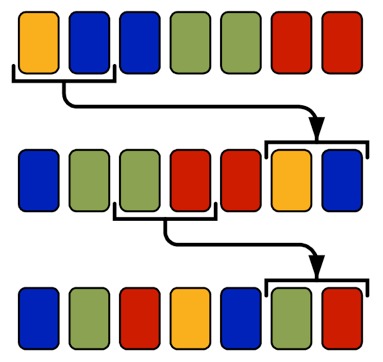
, 1122333344 3 ( 33), – 6. M = ⌈K / 2⌉.
( ) :
- K — ( ). , «» A, «» B, — C. |A| + |B| + |C| = |K|, |A| + |C| = |B| = M. 1122333344 AABBBC.
: (B, C), , — (A, B). , (B, C)* (A, B)*, * — .
:
1122333344 (AABBC) ->1122333-4.34 (AAB) -> 1-2333-4.3412 (BB)
( , . – )
, . : |C| > 0, C , B. |C| = 0, (A, B)*, B . - K — . . A, , A-. C, C- , .
, ⌈K / 2⌉. , , «» ( ). .
. Q.
- Q = 0. , .
- Q > ⌈N / 2⌉, . , Q−1 , .
- Q = ⌈N / 2⌉ . , . :
- a A- ,
- b = Q B-
- c C- .
, A- C-- a = 0 . c = N − Q = ⌊N / 2⌋, , , b c , .
- = 0 . .
- a > 0, b > 0 - a − 1 , B: b − 1, C: c − 1. (a − 1) + (c − 1) = N − Q − 2, Q − 1 , , .
- M < ⌊ ( N + 1) / 2 ⌋ . ( ), , .
, ( ) (C 1 , C 2 ). , , . , .
, . Z, (X, Z) Z , Z Z (X 1 , Z) (X 2 , Z)…. Z- , (X, Y) , (X k , Z) (X k+1 , Y), X k+1 ≠ Z.
, (X, Z) X Z (M). M ≠ Z, Z (X, Z) (Z, ...) , Z M, (X, Z) (M, Z).
, , ⌈K / 2⌉ .
, , , . , O(N log N). , - , , . , , , : . O(n), .
« » .
():
N . , , .
, . , . , , , . , , .
, .
, , .
, .
3 258 , –1000 1000, .
Russian Code Cup .
— .
.
, . , , , . , .
, . , .
, . , , , , .
, . , , .
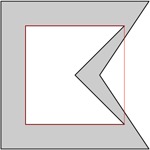
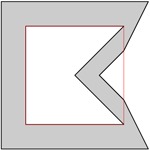
, . , . , . .
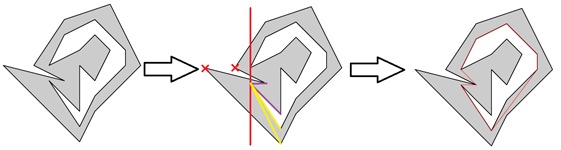
. , — . .
O(n 3 ) , O(n 2 ) O(n) . O(n) O(n 2 ) O(n 2 ). , O(n 3 ).
« » . , 93- .
Russian Code Cup 2012 . , , , - ( , , ), – - ( ) . , , , . , , , , ?
Director of Research and Education
Mail.Ru Group
Source: https://habr.com/ru/post/151876/
All Articles