The topic of prefix search trees has already been raised a number of times. Here , for example, it briefly describes what a prefix tree is and why it is needed, and discusses the main operations on such trees (search, insert, delete). Unfortunately, nothing is said about the implementation. This recent post discusses the Pitona datrie library, which is the cython wrapper of the libdatrie library. The last link has a good description of the implementation of partially compressed prefix trees in the form of deterministic finite automata (using arrays). I decided to add my five kopecks to this topic, having considered the implementation of C ++ prefix trees using pointers. In addition, there was another goal - to compare the search for strings with each other using a balanced binary search tree ( AVL-tree ) and a compressed prefix tree.

Introduction

Recall that a prefix tree is a data structure intended for storing objects with a bitwise structure, for example, strings. Next, we will consider the implementation of prefix trees to store exactly the lines in the ASCII alphabet, each line ends with a terminal character that is not found anywhere else in the line. In the figures and examples, the terminal symbol will be denoted by a dollar sign, and in the code, a zero symbol (thus, in our implementation, the strings will be standard C strings, which will allow us to use the standard library string.h). On the other alphabets all the following should be transferred elementary.
')
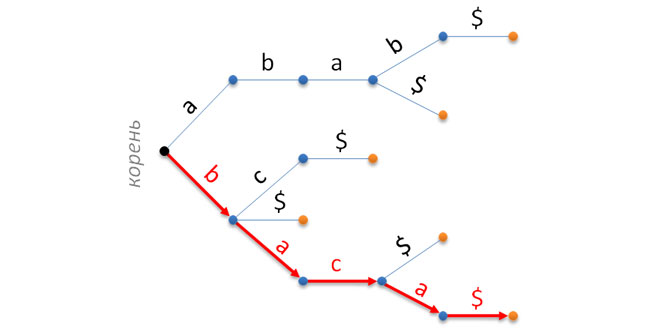
In the usual prefix tree, each edge is assigned a symbol, in the vertices there is a different service (or user) information stored. Thus, any path from the root of a tree to some of its leaves defines exactly one line. It is believed that this string is stored in a given tree. For example, in the following image, the prefix tree stores the next set of lines {abab $, aba $, bc $, b $, bac $, baca $}. The root is on the left, the leaves (their number coincides with the number of rows) is on the right. The path corresponding to the baca $ line is highlighted in red.



An attentive reader will easily notice that in this version the prefix tree is a usual deterministic finite automaton , the receiving states of which correspond to the leaves of the tree. Actually, the implementation of prefix trees in the libdatrie library is built on this consideration. The automaton itself is represented using arrays.

To reduce the size of the machine, the tree view is used in a partially compressed form, when all tree “tails” (areas without branches containing leaves) are packed in rows (figure a below). It is possible to go further and compress all chains without branches in general in the same way (Figure b ). In this case, the tree ceases to be a finite automaton (or rather, it remains an automaton, but above the alphabet of strings, not characters) and its implementation using arrays becomes problematic - working with the tree as with an automaton essentially relies on the fact that the size of the alphabet is finite and that for any character it is possible to determine its sequence number in this alphabet in O (1) time (with strings such a technique will not work). However, in the case of implementation of pointers problems with storing lines should not arise.

Tree view using pointers

So, we will represent the edges of the tree with pointers. First of all, we note that in this case it is not very convenient to store information in the edges of the tree, to put it mildly. Therefore, we move the chains of characters from the edges to the vertices (using the obvious property of the oriented tree — exactly any edge enters any node except the root node). We get just such a structure.



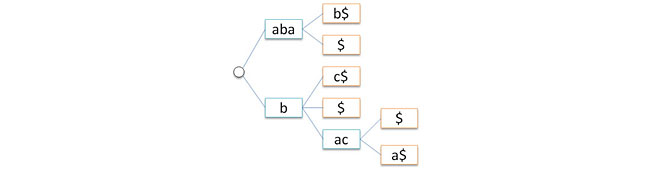
Another problem is the outgoing degree of a tree node can be arbitrary (up to the size of the alphabet used). To solve this problem, we apply the standard method, namely, we will store in each node a list of child nodes. The list will be simply connected and we will keep in the node only the head of the list (the eldest daughter). This will allow us at the same time to abandon the empty root. Now the tree will be represented by a pointer to the head of the list of child nodes of the old root (that is, we replace the tree with the forest). Thus, each node will now contain exactly two pointers: link - to the eldest child node, next - to its younger sister. The following figure shows the process of such a transformation, the blue arrows correspond to the link signs, the red arrows to the next signs.



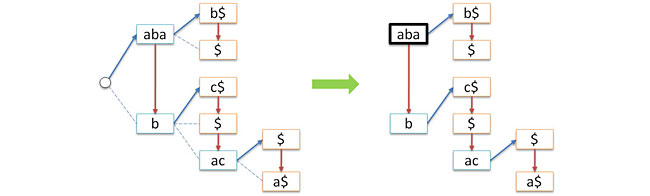
In the future, to understand the logic of working with a tree, it is useful to keep in mind the diagram shown in the figure on the left, while the actual tree representation will be as shown on the right.

So, imperceptibly, we have moved from a tree with a variable outgoing degree (a general tree) to a binary tree , in which the pointers to the right and left subtrees are played by the pointers link and next. The following picture clearly demonstrates this.



Now you can go to the implementation. A tree node is a string of key symbols, its length is len (the string does not have to end with terminal symbols, so you need to know its length explicitly), and two pointers, link and next. Plus a minimal constructor that creates a trivial tree consisting of one node with a given key (for copying characters we will use the standard function strncpy), and an even more minimal destructor.

struct node //      { char* key; int len; node* link; node* next; node(char* x, int n) : len(n), link(0), next(0) { key = new char[n]; strncpy(key,x,n); } ~node() { delete[] key; } }; 

Key search

The first operation we consider is the operation of inserting a new line into the prefix tree. The idea of ​​the search is standard. Moving from the root of the tree. If the root is empty, then the search is unsuccessful. Otherwise, compare the key key in the node with the current row x. To do this, we use the following function, which calculates the length of the greatest common prefix of two lines of a given length.

 int prefix(char* x, int n, char* key, int m) //      x  key { for( int k=0; k<n; k++ ) if( k==m || x[k]!=key[k] ) return k; return n; } 

In the case of a search, we are interested in three cases:

1. the common prefix can be empty, then you have to recursively continue the search in the younger sister of this node, i.e follow the link next;
2. the common prefix is ​​equal to the search string x - the search is successful, the node is found (here we essentially use the fact that the end of the string due to the presence of a terminal symbol in it can only be found in a leaf of the tree);
3. the common prefix coincides with the key, but does not coincide with x - we recursively follow the link link to the senior child node, passing it the search string x without the prefix found.

If there is a common prefix, but does not match the key, the search is also unsuccessful.

 node* find(node* t, char* x, int n=0) //   x   t { if( !n ) n = strlen(x)+1; if( !t ) return 0; int k = prefix(x,n,t->key,t->len); if( k==0 ) return find(t->next,x,n); //    if( k==n ) return t; if( k==t->len ) return find(t->link,x+k,nk); //     return 0; } 

The length n of the string x defaults to zero (and then it is explicitly computed) so that you can call the search function, indicating only the root of the tree and the string to search for:

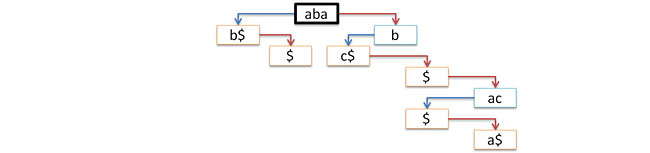
  ... node* p = find(t,"baca"); ... 

The following figure shows the process of finding three lines (one successful and two not so) in the above tree.



Note that the search function, if successful, returns a pointer to the leaf of the tree where the search ended. It is in this node should be located all the information associated with the desired line.

Insert keys

Inserting a new key (as in binary search trees) is very similar to a key search. Naturally with a few differences. First, in the case of an empty tree, you need to create a node (a trivial tree) with the specified key and return a pointer to this node. Secondly, if the length of the common prefix of the current key and the current string x is more than zero, but less than the key length (the second case of non-daily search), then the current node should be split into two, leaving the found prefix in the parent node and placing the remaining p node in the child node p part of the key. This operation is implemented by the split function. After splitting, you need to continue the process of inserting the string x in the node p without the prefix found.



Node Split Code:

 void split(node* t, int k) //   t  k-   { node* p = new node(t->key+k,t->len-k); p->link = t->link; t->link = p; char* a = new char[k]; strncpy(a,t->key,k); delete[] t->key; t->key = a; t->len = k; } 

Insert code:

 node* insert(node* t, char* x, int n=0) //   x   t { if( !n ) n = strlen(x)+1; if( !t ) return new node(x,n); int k = prefix(x,n,t->key,t->len); if( k==0 ) t->next = insert(t->next,x,n); else if( k<n ) { if( k<t->len ) //   ? split(t,k); t->link = insert(t->link,x+k,nk); } return t; } 

An example of inserting the abaca $ and abcd $ keys into the above tree is shown in the following figure.



Note that if the specified string x is already contained in the tree, then no insertion will be made. From this point of view, the prefix tree behaves like a respectable set.

Deleting keys

As usual, deleting a key is the most difficult operation. Although in the case of a prefix tree, everything does not look so scary. The point is that deleting a key removes just one leaf node corresponding to the suffix of some key to be deleted. First we find this node, if the search is successful, then we delete it and return a pointer to the younger sister of this node (he has no daughters, he is a sheet, but there may be sisters).



In principle, the deletion process could have been completed, but a small problem arises - after deleting a node in the tree, a chain of two nodes t and p can form, in which the first node t has a single child node p. Therefore, if we want to keep the tree in a compressed form, then we need to combine these two nodes into one, after performing the merge operation.



The merge function code is quite trivial - we form a new key, re-hang the subtree of node p to node t, delete the node p:

 void join(node* t) //   t  t->link { node* p = t->link; char* a = new char[t->len+p->len]; strncpy(a,t->key,t->len); strncpy(a+t->len,p->key,p->len); delete[] t->key; t->key = a; t->len += p->len; t->link = p->link; delete p; } 

The senior node is responsible for the merger, because the junior has no information about his parent. The criteria for a merge is 1) deleting a key by the link link, and not by next; 2) after deletion, the new link has no link next (the child node is only one, which means it can be merged with the current one).

 node* remove(node* t, char* x, int n=0) //   x   t { if( !n ) n = strlen(x)+1; if( !t ) return 0; int k = prefix(x,n,t->key,t->len); if( k==n ) //   { znode* p = t->next; delete t; return p; } if( k==0 ) t->next = remove(t->next, x, n); else if( k==t->len ) { t->link = remove(t->link, x+k, nk); if( t->link && !t->link->next ) //   t   ? join(t); } return t; } 

Examples of deleting keys without merging:



and merge:

Efficiency

A small numerical study was conducted comparing AVL-trees and prefix trees with respect to operation time and consumed memory. The results turned out to be somewhat discouraging for me (perhaps the curvature of someone’s hands might have affected). But in order ... For testing, 8 test rows were formed. Their brief characteristics are listed in the table.



First of all, the time of building a tree was measured by a given set of rows and the time it took to search for all the keys from the same set (that is, only a successful search). The following graph shows a comparison of the construction time of the AVL-tree and the prefix tree. It can be seen that the prefix tree is built a little faster.



The following graph shows the comparison of time spent searching for all the available keys for the same two trees. And here everything turned out to be wrong. A balanced binary tree spends on search about two times less time than a prefix one.



Finally, it was interesting to see what the cost of memory per symbol is. The results are shown in the following graph.



On average, for both types of trees, about 2 bytes per character are obtained, which in my opinion is not very bad. Interestingly, in the case of flags, a prefix tree spends less than one byte per character (many common long prefixes).

So, a clear winner was not identified as a result. It would be necessary to make a comparison of the working time of these two trees relative to the number of rows, but judging from the above graphs, nothing revolutionary can be expected anyway. And, of course, it would be interesting to compare these two campaigns with hash tables ...

Thanks for attention!

I would be grateful for comments and comments!