Details on random and pseudorandom number generators
On Habré and the network, articles devoted to vulnerabilities in random number generators often began to appear. This topic is extremely extensive and is one of the main cryptography. Under the cut is a description of random numbers from A to Z. The article is the result of a free translation of a cycle of articles from one Western blog and personal additions of the author. The main goal is to get feedback and share knowledge.

Random number generators are a key part of web security. A small list of applications:
Let there be a sequence of numbers:

The sequence of digits in Pi is considered random. Let the generator be based on the output bits of the representation of the number Pi, starting from some unknown point. Such a generator, possibly, will pass the “test for the next bit” , since the PI, apparently, is a random sequence. However, this approach is not critically reliable - if the cryptanalyst determines which bit of Pi is currently being used, he will be able to calculate all the preceding and subsequent bits.
This example imposes another restriction on random number generators. A cryptanalyst should not be able to predict the operation of a random number generator.
')
The entropy sources are used to accumulate the entropy and then obtain from it the initial value (initial value, seed) needed by the random number generator (RNG) to generate random numbers. The PRNG uses a single initial value, from which its pseudo-randomness follows, and the RNG always generates a random number, having at the beginning a high-quality random variable provided by various sources of entropy.
Entropy is a measure of disorder. Informational entropy is a measure of uncertainty or unpredictability of information.
We can say that RNG = PRNG + source of entropy.
A common method for generating pseudo-random numbers that does not have cryptographic security. The linear congruential method consists in calculating the members of a linear recurrent sequence modulo some natural number m given by the following formula:
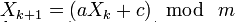
where a (multiplier), c (addend), m (mask) are some integer coefficients. The resulting sequence depends on the choice of the starting number (seed) X0 and for its different values, different sequences of random numbers are obtained.
To select the coefficients, there are properties that allow you to maximize the length of the period (the maximum length is equal to m), that is, the moment from which the generator will cycle around [1].
Let the generator produce several random numbers X0, X1, X2, X3. It turns out the system of equations

Having solved this system, we can determine the coefficients a, c, m. According to Wikipedia [8] , this system has a solution, but it was not possible to decide on its own or find a solution. I would be very grateful for any help in this direction.
The main algorithm for predicting numbers for a linearly congruent method is Plumstead's, an implementation that can be found here [4] (there is an online launch) and here [5] . A description of the algorithm can be found in [9] .
A simple implementation of the congruential method in Java.
By sending 20 numbers to the site [4] , you can most likely get the following. The more numbers, the more likely.
Many programming languages, such as C (rand), C ++ (rand), and Java, use LPRNG. Consider how you can hack on the example of java.utils.Random . Going to the source code (jdk1.7) of this class, you can see the constants used
The java.utils.Randon.nextInt () method looks like this (here bits == 32)
The result is the nextseed shifted to the right by 48-32 = 16 bits. This method is called truncated-bits, which is especially unpleasant when the black-box, you have to add another loop to brute-force. Hacking will be done by brute-force.
Suppose we know two successively generated numbers x1 and x2. Then you need to go through 2 ^ 16 = 65536 variants of oldseed and apply the formula to x1:
until it becomes equal to x2. The code for brute-force might look like this.
The output of this program will be something like this:
It is easy to understand that we did not find the very first seed, but the seed used to generate the second number. To find the original seed, you need to perform several operations that Java used to transform the seed, in the reverse order.
And now in the source code replace
crackingSeed.set (seed);
on
crackingSeed.set (getPreviousSeed (seed));
And that's it, we successfully cracked PRNG in Java.
Consider another non-cryptographic algorithm for generating pseudo-random numbers Mersenne Twister. The main advantages of the algorithm are the generation rate and a huge period of 2 ^ 19937 - 1. This time we will analyze the implementation of the mt_srand () and mt_rand () algorithm in php version 5.4.6 source code.
You may notice that php_mt_reload is called during initialization and after calling php_mt_rand 624 times. Start hacking from the end, reversing the transformations at the end of the php_mt_rand () function. Consider (s1 ^ (s1 >> 18)). In a binary representation, the operation looks like this:
101101110101111001 11111001110010 s1
00000000000000000010110111010111100111111001110010 s1 >> 18
101101110101111001 01001110100101 s1 ^ (s1 >> 18)
It can be seen that the first 18 bits (bold) remained unchanged.
Write two functions to invert the bit shift and xor
Then the code to invert the last lines of the php_mt_rand () function will look like this
If we have 624 consecutive numbers generated by Mersenne Twister, then applying this algorithm to these consecutive numbers, we get the full Mersenne Twister state, and we can easily determine each subsequent value by running php_mt_reload for a known set of values.
If you think that there is nothing to break, then you are deeply mistaken. One of the interesting directions is the Adobe Flash (Action Script 3.0) random number generator. Its feature is the closeness of the source code and the absence of the task of the seed. His main interest is in many online casinos and online poker.
There are many sequences of numbers, ranging from the dollar to the amount of time spent in traffic every day. And finding a pattern in such data is not an easy task.
For any random variable, you can specify the distribution. Transferring to the example with cards, you can make aces fall more often than nines. Below are a few examples for triangular distribution and exponential distribution.
Let us give an example of generating a random variable with a triangular distribution [7] in the language C99.
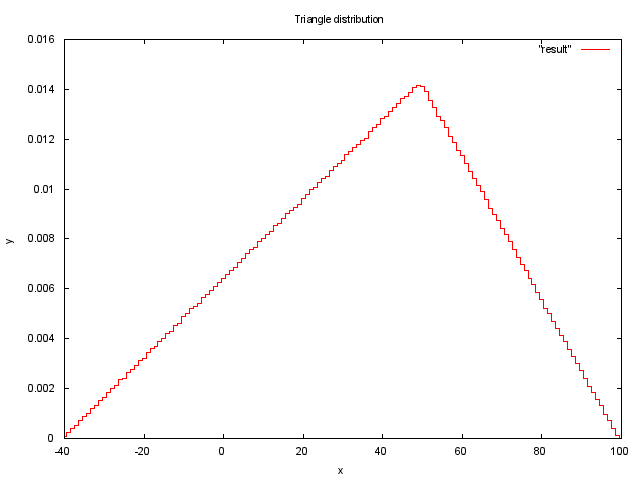
In this case, we take a random variable rand () and assign it a distribution, based on the triangular distribution function. For parameters a = -40, b = 100, c = 50, the 10,000,000 measurement graph will look like this
Suppose you want to get a sensor of exponentially distributed random variables. In this case, F (x) = 1 - exp (-lambda * x). Then from the solution of the equation y = 1 - exp (-lambda * x) we get x = -log (1-y) / lambda.
You can see that the expression under the sign of the logarithm in the last formula has a uniform distribution on the interval [0,1), which allows you to get another, but also distributed sequence by the formula: x = -log (y) / lambda, where y is a random variable (rand ()).
Some developers believe that if they hide the generation method they use or invent their own, then this is enough for protection. This is a very common misconception. It should be remembered that there are special methods and techniques for finding dependencies in a sequence of numbers.
One of the known tests is the test for the next bit - a test that serves to test pseudo-random number generators for cryptographic resistance. The test says that there should not be a polynomial algorithm that, knowing the first k bits of a random sequence, can predict k + 1 bits with a probability greater than ½.
In cryptography theory, a separate problem is the determination of how random the sequence of numbers or bits generated by a generator is. As a rule, various statistical tests are used for this purpose, such as DIEHARD or NIST. Andrew Yao in 1982 proved that the generator, which passed the “test for the next bit”, will also pass any other statistical randomness tests that can be performed in polynomial time.
On the Internet [10] you can pass the DIEHARD tests and many others to determine the criterion resistance of the algorithm.
[1] Donald Knut, The Art of Programming (Volume 2. Algorithms Computed)
[2] Bruce Schneier, Applied Cryptography (Chapter 16)
[4] www.staff.uni-mainz.de/pommeren/Kryptologie/Bitstrom/2_Analyse/LCGcrack.html
[5] www.staff.uni-mainz.de/pommeren/Kryptologie99/English.html
[6] en.wikipedia.org/wiki/Mersenne_twister
[7] en.wikipedia.org/wiki/Triangular_distribution
[8] en.wikipedia.org/wiki/Linear_congruent_method
[9] zaic101.ru/files/728/using_linear_congruential_generators_for_cryptographic_purposes.pdf
[10] www.cacert.at/random
[11] www.cs.berkeley.edu/~daw/papers/ddj-netscape.html
[12] www.computerworld.com/s/article/9048438/Microsoft_confirms_that_XP_contains_random_number_generator_bug
[13] An interesting example of generation via md5 is described raz0r.name/articles/magiya-sluchajnyx-chisel-chast-2/comment-page-1
jazzy.id.au/default/2010/09/20/cracking_random_number_generators_part_1.html
jazzy.id.au/default/2010/09/21/cracking_random_number_generators_part_2.html
jazzy.id.au/default/2010/09/22/cracking_random_number_generators_part_3.html
jazzy.id.au/default/2010/09/25/cracking_random_number_generators_part_4.html

Introduction
Random number generators are a key part of web security. A small list of applications:
- Session Generators (PHPSESSID)
- Generate text for captcha
- Encryption
- Salt generation for storing passwords in irreversible form
- Password generator
- The procedure for the distribution of cards in online casinos
How to distinguish a random sequence of numbers from non-random?
Let there be a sequence of numbers:
1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 . Is it random? There is a strict definition for a random variable. A random variable is a quantity that as a result of experience takes one of a multitude of values, and the appearance of one or another value of this quantity before its measurement cannot be accurately predicted. But it does not help to answer our question, because we do not have enough information to answer. Now let's say that these numbers turned out to be a set of one of the top lines of the keyboard. “Of course not random” - exclaim you and immediately call the following number and you will be absolutely right. The sequence will be random only if there is no dependency between characters. For example, if these symbols appeared as a result of pulling the kegs into a lotto, the sequence would be random.Slightly more complex example or number Pi

The sequence of digits in Pi is considered random. Let the generator be based on the output bits of the representation of the number Pi, starting from some unknown point. Such a generator, possibly, will pass the “test for the next bit” , since the PI, apparently, is a random sequence. However, this approach is not critically reliable - if the cryptanalyst determines which bit of Pi is currently being used, he will be able to calculate all the preceding and subsequent bits.
This example imposes another restriction on random number generators. A cryptanalyst should not be able to predict the operation of a random number generator.
')
The difference between the pseudorandom number generator (PRNG) and the random number generator (PRNG)
The entropy sources are used to accumulate the entropy and then obtain from it the initial value (initial value, seed) needed by the random number generator (RNG) to generate random numbers. The PRNG uses a single initial value, from which its pseudo-randomness follows, and the RNG always generates a random number, having at the beginning a high-quality random variable provided by various sources of entropy.
Entropy is a measure of disorder. Informational entropy is a measure of uncertainty or unpredictability of information.
We can say that RNG = PRNG + source of entropy.
PRNG vulnerabilities
- Predictable dependency between numbers.
- Predictable initial value of the generator.
- Small period length of the generated sequence of random numbers, after which the generator loops.
Linear congruent PRNG (LCPRNG)
A common method for generating pseudo-random numbers that does not have cryptographic security. The linear congruential method consists in calculating the members of a linear recurrent sequence modulo some natural number m given by the following formula:
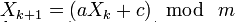
where a (multiplier), c (addend), m (mask) are some integer coefficients. The resulting sequence depends on the choice of the starting number (seed) X0 and for its different values, different sequences of random numbers are obtained.
To select the coefficients, there are properties that allow you to maximize the length of the period (the maximum length is equal to m), that is, the moment from which the generator will cycle around [1].
Let the generator produce several random numbers X0, X1, X2, X3. It turns out the system of equations

Having solved this system, we can determine the coefficients a, c, m. According to Wikipedia [8] , this system has a solution, but it was not possible to decide on its own or find a solution. I would be very grateful for any help in this direction.
Prediction of results of the linear-congruential method
The main algorithm for predicting numbers for a linearly congruent method is Plumstead's, an implementation that can be found here [4] (there is an online launch) and here [5] . A description of the algorithm can be found in [9] .
A simple implementation of the congruential method in Java.
public static int a = 45; public static int c = 21; public static int m = 67; public static int seed = 2; public static int getRand() { seed = (a * seed + c) % m; return seed; } public static void main(String[] args) { for(int i=0; i<30; i++) System.out.println(getRand()); } By sending 20 numbers to the site [4] , you can most likely get the following. The more numbers, the more likely.
Hacking a built-in random number generator in Java
Many programming languages, such as C (rand), C ++ (rand), and Java, use LPRNG. Consider how you can hack on the example of java.utils.Random . Going to the source code (jdk1.7) of this class, you can see the constants used
private static final long multiplier = 0x5DEECE66DL; // 25214903917 private static final long addend = 0xBL; // 11 private static final long mask = (1L << 48) - 1; // 281474976710655 = 2^48 – 1 The java.utils.Randon.nextInt () method looks like this (here bits == 32)
protected int next(int bits) { long oldseed, nextseed; AtomicLong seed = this.seed; do { oldseed = seed.get(); nextseed = (oldseed * multiplier + addend) & mask; } while (!seed.compareAndSet(oldseed, nextseed)); return (int)(nextseed >>> (48 - bits)); } The result is the nextseed shifted to the right by 48-32 = 16 bits. This method is called truncated-bits, which is especially unpleasant when the black-box, you have to add another loop to brute-force. Hacking will be done by brute-force.
Suppose we know two successively generated numbers x1 and x2. Then you need to go through 2 ^ 16 = 65536 variants of oldseed and apply the formula to x1:
((x1*multiplier + addend) & mask) << 16 until it becomes equal to x2. The code for brute-force might look like this.
import java.lang.reflect.Field; import java.util.Random; import java.util.concurrent.atomic.AtomicLong; public class PasswordCracking { public static final long multiplier = 0x5DEECE66DL; public static final long addend = 0xBL; public static final long mask = (1L << 48) - 1; public static void main(String[] args) { Random random = new Random(); long v1 = random.nextInt(); long v2 = random.nextInt(); long v3 = random.nextInt(); long v4 = random.nextInt(); System.out.println("v1=" + v1 + "\nv2=" + v2 + "\nv3=" + v3 + "\nv4=" + v4); // brute-force seed for (int i = 0; i < 65536; i++) { long seed = (((long) v1) << 16) + i; int nextInt = (int)(((seed * multiplier + addend) & mask) >>> 16); if (nextInt == v2) { System.out.println("Seed found: " + seed); Random crackingRandom = new Random(); try { /* set the seed for Random to be convinced that we have found the right seed because constructor Random (long seed) uses the private static long initialScramble (long seed) { return (seed ^ multiplier) & mask; } for simplicity will use Reflection */ Field privateSeedField = Random.class.getDeclaredField("seed"); privateSeedField.setAccessible(true); AtomicLong crackingSeed = (AtomicLong)privateSeedField.get(crackingRandom); crackingSeed.set(seed); }catch(Exception e) { System.out.println(e.toString()); System.exit(1); } long cv1 = crackingRandom.nextInt(); long cv2 = crackingRandom.nextInt(); long cv3 = crackingRandom.nextInt(); long cv4 = crackingRandom.nextInt(); System.out.println("Set fiend seed and generate random numbers"); System.out.println("cv1=" + cv1 + "\ncv2=" + cv2 + "\ncv3=" + cv3 + "\ncv4=" + cv4); break; } } } } The output of this program will be something like this:
v1 = -1184958941 v2 = 274285127 v3 = -1566774765 v4 = 30466408 Seed found: -77657469128792 Set fiend seed and generate random numbers cv1 = 274285127 cv2 = -1566774765 cv3 = 30466408 cv4 = -803980434 It is easy to understand that we did not find the very first seed, but the seed used to generate the second number. To find the original seed, you need to perform several operations that Java used to transform the seed, in the reverse order.
public static long getPreviousSeed(long prevSeed) { long seed = prevSeed; // reverse the addend from the seed seed -= addend; // reverse the addend long result = 0; // iterate through the seeds bits for (int i = 0; i < 48; i++) { long mask = 1L << i; // find the next bit long bit = seed & mask; // add it to the result result |= bit; if (bit == mask) { // if the bit was 1, subtract its effects from the seed seed -= multiplier << i; } } System.out.println("Previous seed: " + result); return result; } And now in the source code replace
crackingSeed.set (seed);
on
crackingSeed.set (getPreviousSeed (seed));
And that's it, we successfully cracked PRNG in Java.
Hacking PRNG Mersenne twister in PHP
Consider another non-cryptographic algorithm for generating pseudo-random numbers Mersenne Twister. The main advantages of the algorithm are the generation rate and a huge period of 2 ^ 19937 - 1. This time we will analyze the implementation of the mt_srand () and mt_rand () algorithm in php version 5.4.6 source code.
Contents of the file /ext/standard/basic_functions.h
#define MT_N (624) /* rand.c */ php_uint32 state[MT_N+1]; /* state vector + 1 extra to not violate ANSI C */ php_uint32 *next; /* next random value is computed from here */ int left; /* can *next++ this many times before reloading */ unsigned int rand_seed; /* Seed for rand(), in ts version */ zend_bool rand_is_seeded; /* Whether rand() has been seeded */ zend_bool mt_rand_is_seeded; /* Whether mt_rand() has been seeded */ Content of file / extra/standard/rand.c:
#define N MT_N /* length of state vector */ #define M (397) /* a period parameter */ #define hiBit(u) ((u) & 0x80000000U) /* mask all but highest bit of u */ #define loBit(u) ((u) & 0x00000001U) /* mask all but lowest bit of u */ #define loBits(u) ((u) & 0x7FFFFFFFU) /* mask the highest bit of u */ #define mixBits(u, v) (hiBit(u)|loBits(v)) /* move hi bit of u to hi bit of v */ #define twist(m,u,v) (m ^ (mixBits(u,v)>>1) ^ ((php_uint32)(-(php_int32)(loBit(u))) & 0x9908b0dfU)) /* {{{ php_mt_reload */ static inline void php_mt_reload(TSRMLS_D) { /* Generate N new values in state Made clearer and faster by Matthew Bellew (matthew.bellew@home.com) */ register php_uint32 *state = BG(state); register php_uint32 *p = state; register int i; for (i = N - M; i--; ++p) *p = twist(p[M], p[0], p[1]); for (i = M; --i; ++p) *p = twist(p[MN], p[0], p[1]); *p = twist(p[MN], p[0], state[0]); BG(left) = N; BG(next) = state; } /* }}} */ /* {{{ php_mt_initialize */ static inline void php_mt_initialize(php_uint32 seed, php_uint32 *state) { /* Initialize generator state with seed See Knuth TAOCP Vol 2, 3rd Ed, p.106 for multiplier. In previous versions, most significant bits (MSBs) of the seed affect only MSBs of the state array. Modified 9 Jan 2002 by Makoto Matsumoto. */ register php_uint32 *s = state; register php_uint32 *r = state; register int i = 1; *s++ = seed & 0xffffffffU; for( ; i < N; ++i ) { *s++ = ( 1812433253U * ( *r ^ (*r >> 30) ) + i ) & 0xffffffffU; r++; } } /* }}} */ /* {{{ php_mt_srand */ PHPAPI void php_mt_srand(php_uint32 seed TSRMLS_DC) { /* Seed the generator with a simple uint32 */ php_mt_initialize(seed, BG(state)); php_mt_reload(TSRMLS_C); /* Seed only once */ BG(mt_rand_is_seeded) = 1; } /* }}} */ /* {{{ php_mt_rand */ PHPAPI php_uint32 php_mt_rand(TSRMLS_D) { /* Pull a 32-bit integer from the generator state Every other access function simply transforms the numbers extracted here */ register php_uint32 s1; if (BG(left) == 0) { php_mt_reload(TSRMLS_C); } --BG(left); s1 = *BG(next)++; s1 ^= (s1 >> 11); s1 ^= (s1 << 7) & 0x9d2c5680U; s1 ^= (s1 << 15) & 0xefc60000U; return ( s1 ^ (s1 >> 18) ); } You may notice that php_mt_reload is called during initialization and after calling php_mt_rand 624 times. Start hacking from the end, reversing the transformations at the end of the php_mt_rand () function. Consider (s1 ^ (s1 >> 18)). In a binary representation, the operation looks like this:
101101110101111001 11111001110010 s1
00000000000000000010110111010111100111111001110010 s1 >> 18
101101110101111001 01001110100101 s1 ^ (s1 >> 18)
It can be seen that the first 18 bits (bold) remained unchanged.
Write two functions to invert the bit shift and xor
public static long unBitshiftRightXor(long value, long shift) { // we part of the value we are up to (with a width of shift bits) long i = 0; // we accumulate the result here long result = 0; // iterate until we've done the full 32 bits while (i * shift < 32) { // create a mask for this part long partMask = (-1 << (32 - shift)) >>> (shift * i); // obtain the part long part = value & partMask; // unapply the xor from the next part of the integer value ^= part >>> shift; // add the part to the result result |= part; i++; } return result; } public static long unBitshiftLeftXor(long value, long shift, long mask) { // we part of the value we are up to (with a width of shift bits) long i = 0; // we accumulate the result here long result = 0; // iterate until we've done the full 32 bits while (i * shift < 32) { // create a mask for this part long partMask = (-1 >>> (32 - shift)) << (shift * i); // obtain the part long part = value & partMask; // unapply the xor from the next part of the integer value ^= (part << shift) & mask; // add the part to the result result |= part; i++; } return result; } Then the code to invert the last lines of the php_mt_rand () function will look like this
long value = output; value = unBitshiftRightXor(value, 18); value = unBitshiftLeftXor(value, 15, 0xefc60000); value = unBitshiftLeftXor(value, 7, 0x9d2c5680); value = unBitshiftRightXor(value, 11); If we have 624 consecutive numbers generated by Mersenne Twister, then applying this algorithm to these consecutive numbers, we get the full Mersenne Twister state, and we can easily determine each subsequent value by running php_mt_reload for a known set of values.
Hacking area
If you think that there is nothing to break, then you are deeply mistaken. One of the interesting directions is the Adobe Flash (Action Script 3.0) random number generator. Its feature is the closeness of the source code and the absence of the task of the seed. His main interest is in many online casinos and online poker.
There are many sequences of numbers, ranging from the dollar to the amount of time spent in traffic every day. And finding a pattern in such data is not an easy task.
Distribution job for pseudo-random number generator
For any random variable, you can specify the distribution. Transferring to the example with cards, you can make aces fall more often than nines. Below are a few examples for triangular distribution and exponential distribution.
Triangular distribution
Let us give an example of generating a random variable with a triangular distribution [7] in the language C99.
double triangular(double a, double b, double c) { double U = rand() / (double) RAND_MAX; double F = (c - a) / (b - a); if (U <= F) return a + sqrt(U * (b - a) * (c - a)); else return b - sqrt((1 - U) * (b - a) * (b - c)); } In this case, we take a random variable rand () and assign it a distribution, based on the triangular distribution function. For parameters a = -40, b = 100, c = 50, the 10,000,000 measurement graph will look like this

Exponential distribution
Suppose you want to get a sensor of exponentially distributed random variables. In this case, F (x) = 1 - exp (-lambda * x). Then from the solution of the equation y = 1 - exp (-lambda * x) we get x = -log (1-y) / lambda.
You can see that the expression under the sign of the logarithm in the last formula has a uniform distribution on the interval [0,1), which allows you to get another, but also distributed sequence by the formula: x = -log (y) / lambda, where y is a random variable (rand ()).
PRNG tests
Some developers believe that if they hide the generation method they use or invent their own, then this is enough for protection. This is a very common misconception. It should be remembered that there are special methods and techniques for finding dependencies in a sequence of numbers.
One of the known tests is the test for the next bit - a test that serves to test pseudo-random number generators for cryptographic resistance. The test says that there should not be a polynomial algorithm that, knowing the first k bits of a random sequence, can predict k + 1 bits with a probability greater than ½.
In cryptography theory, a separate problem is the determination of how random the sequence of numbers or bits generated by a generator is. As a rule, various statistical tests are used for this purpose, such as DIEHARD or NIST. Andrew Yao in 1982 proved that the generator, which passed the “test for the next bit”, will also pass any other statistical randomness tests that can be performed in polynomial time.
On the Internet [10] you can pass the DIEHARD tests and many others to determine the criterion resistance of the algorithm.
Known hacks of random number generators
- Early versions of Netscape's SSL encryption protocol, with low entropy [11]
- PHP vulnerability sessions habrahabr.ru/company/pt/blog/149746
- Microsoft's CryptGenRandom [12]
- Many online casinos have repeatedly become the object of attack through vulnerabilities in the PRNG.
Bibliography
[1] Donald Knut, The Art of Programming (Volume 2. Algorithms Computed)
[2] Bruce Schneier, Applied Cryptography (Chapter 16)
[4] www.staff.uni-mainz.de/pommeren/Kryptologie/Bitstrom/2_Analyse/LCGcrack.html
[5] www.staff.uni-mainz.de/pommeren/Kryptologie99/English.html
[6] en.wikipedia.org/wiki/Mersenne_twister
[7] en.wikipedia.org/wiki/Triangular_distribution
[8] en.wikipedia.org/wiki/Linear_congruent_method
[9] zaic101.ru/files/728/using_linear_congruential_generators_for_cryptographic_purposes.pdf
[10] www.cacert.at/random
[11] www.cs.berkeley.edu/~daw/papers/ddj-netscape.html
[12] www.computerworld.com/s/article/9048438/Microsoft_confirms_that_XP_contains_random_number_generator_bug
[13] An interesting example of generation via md5 is described raz0r.name/articles/magiya-sluchajnyx-chisel-chast-2/comment-page-1
Original
jazzy.id.au/default/2010/09/20/cracking_random_number_generators_part_1.html
jazzy.id.au/default/2010/09/21/cracking_random_number_generators_part_2.html
jazzy.id.au/default/2010/09/22/cracking_random_number_generators_part_3.html
jazzy.id.au/default/2010/09/25/cracking_random_number_generators_part_4.html
Source: https://habr.com/ru/post/151187/
All Articles