The solution of the traveling salesman problem by recursive brute force
We formulate the problem.
Given N nodes located on the plane. An input node (Bx) and output node (Out) are specified. You must discover the shortest path that encompasses all nodes, starting at the input node, ending at the output node, and passing through each node only once.
There are opinions that the task of a traveling salesman can be formulated in two more ways:
1. It is necessary to discover the shortest Hamiltonian cycle.
2. It is necessary to find the shortest path starting at a given node.
However, both of these formulations on closer examination turn out to be special cases of the original formulation.
Formulation 1 implies that the input node can be any node, and the output - one of the closest to it. That requires a complete search of all the closest nodes to a randomly selected node.
Formulation 2 implies that the input node is defined, and the output node can be any. What requires a complete enumeration of all output nodes, followed by the selection of the shortest path of all the shortest.
Therefore, we will focus on the original formulation, and we will solve the problem in a general form.
It is generally recognized that the traveling salesman problem in general is guaranteed to be solved optimally only by exhaustive search of all the options.
In the algorithmic implementation of the complete iteration, it is possible to use two conditions that reduce the iteration time and cut off the obviously non-optimal paths, namely:
1. When constructing the next version of the path, calculate its length and if this length exceeds the local minimum of the length already found, skip this variant and all those it generates.
2. If the next selected edge intersects one of the previously constructed edges - skip this option and all those that it generates.
')
The last condition actually prohibits cycles, since if we imagine ourselves in the place of a real traveling salesman, then the intersection of the ribs (despite the fact that in the task it is forbidden to explicitly reuse the nodes) will actually mean the return of the traveling salesman to the place where he was already, which contradicts the definition of the optimal (shortest) of the way.
The optimal solution to the traveling salesman problem on desktops is possible. However, with an increase in the number of nodes, the time spent on a complete search increases exponentially. Thus, on a machine with a quad core processor 2.67 GHz, 10 nodes are calculated on average in 5 milliseconds, 20 nodes in 15 minutes, and calculating the optimal path for 60 nodes will take more than 6 trillion years ...
To circumvent this obstacle, people simply refuse to obtain an optimal solution for large N and instead of the traveling salesman problem they solve some other, very similar, similar problem. Such a method of substitution of the problem is called the “heuristic solution”, although heuristics in each case is no more than a randomly chosen analogy. For example, annealing is a solution to a problem by simulating the cooling of crystallizing substances, a greedy algorithm is an imitation of the behavior of a greedy person, there are methods built by analogy with the behavior of ants, an inflating balloon, etc.
The method of analogy is bad because the full search, as the best solution, is completely discarded and completely replaced by some other method. I believe that it is impossible to do so with scorn with complete enumeration, because this is the only method that is guaranteed to give the correct solution to the problem.
We will try to solve the traveling salesman problem only by complete brute force, replacing it with something else only where it is really necessary for reasons of time.
We will not look for an analogy at random, we will try to solve the traveling salesman’s problem as impartially as possible, without invoking extraneous analogies for help. Let's try to solve a common problem in general. And for this we will call for help only one analogy - an analogy with intelligence in general. How does the human intellect solve complex problems (including the traveling salesman problem)? It splits the original problem into a tree of simpler sub-problems, solves them in the reverse order and gets the result. We will do the same!
It is quite obvious that to simplify the traveling salesman problem in order to solve it by complete brute force in an acceptable time can only be done in one way — by reducing the number of nodes being sorted. And this can also be done in only one way - to merge nodes into groups - over-nodes, over-tasks (sub-tasks).
To set the traveling salesman problem recursively try to look at it recursively.
The main element in this task is a node that contains one edge and one edge:
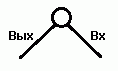
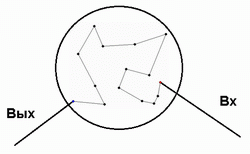
Without invoking extraneous analogies, we immediately notice the analogy with the very formulation of the general problem, in which two “extreme” nodes are set: Bx , which includes the traveling salesman at the start, and Exit , from which the salesman leaves at the finish. We can say that the entire set of nodes N in the problem is one large node, in which the traveling salesman enters and leaves by an edge:
Thus, a general view of the recursive algorithm appears.
1. Set the nodes N.
2. Set the maximum allowable time for solving the problem Tmax.
3. Carry out a benchmark on this machine and determine the dependence of the solution time on the number of nodes with a full search of T (N) options.
4. Based on a given number of nodes N, Tmax and dependencies for T, determine how many groups (over-nodes) a set of N nodes should be split. Or set this number of nodes manually (this is exactly what we will do).
5. Split a set of N nodes into M groups.
6. Perform a complete search for M groups and find the shortest way to connect these groups.
7. After step 6, we have an entry and exit for each group, so we recursively set the salesman problem for each group, i.e. go to step 4, where N is equal to the number of nodes in each group.
8. After exiting recursion, we obtain a suboptimal path for this machine and this Tmax (or a specified number of nodes in the group).
Paragraph 4 is needed so that we do not degrade the algorithm beyond what is necessary. If the machine can perform a complete search for a given number of nodes, then we should allow it to it.
In step 5, it is obviously better to prefer M as much as possible. When M tends to N, we get an ever more accurate solution. The less we move away from complete enumeration, the more accurate our decision. It is possible to choose M according to the table made up of the simplest rough assumption that at each recursion step we will divide the sub-task into groups with the same number of nodes in the group.
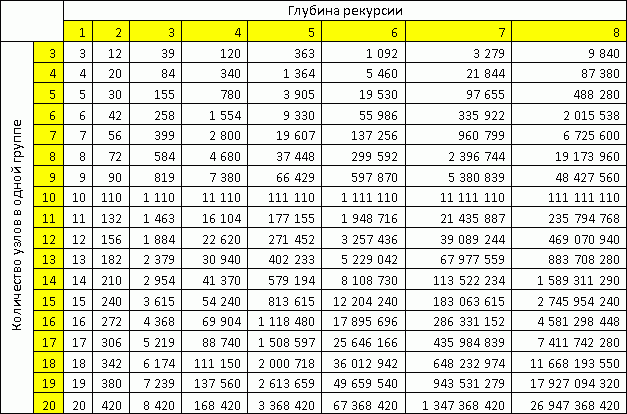
As can be seen from the table, already with 18 nodes in one group, we can process more than 10 billion nodes with a recursion depth of up to 8.
If we want to improve the route found in this way, then we have the following options:
- choose a more productive machine
- increase the allowable time Tmax
- increase the number of groups
- increase recursion nesting. That is, in step 6, it is necessary to split the task into substantially (depending on N) a larger number of groups, but it is not optimal, but to subselect them, but suboptimally. For example, to divide a task from 1000 nodes into 500 groups, but not to search for the shortest way of connecting them by complete brute force (this is too long), but to break groups into sub-groups, for example, into 250 groups and search for a suboptimal path among them. And so on, until we go down to a level where the machine can do a complete bust.
How to combine nodes into groups?
In order not to attract abstract analogies and not to use vague heuristics, we will try to find the answer in the problem itself. It is absolutely clear that initially in the problem we have one group, for which the Bx and Out are set.
To break this task into at least two, we need to allocate among all nodes an intermediate node, which will become an intermediate input / output.
Since we use the Euclidean distance as a sign of optimality in the problem, to detect the new intermediate input / output we need to enter a certain limit on the distance from each node to the already existing input and output. Since we do not know what the limit is, let us mentally take it so large that it turns out that all nodes belong only to the initial group. Now mentally we will gradually reduce this limit. At the same time, one of the nodes that previously belonged to the original group should stand out from it. Regardless of what exactly we take as a limit, this node will be the node that is located at the farthest distance from the initial entry and exit. Therefore, instead of inventing the formula of the limit, we can immediately take the most distant node. After we have found this intermediate entry / exit, we must divide all the remaining nodes between the new two groups so as to ensure that the edges do not intersect.
If we need to divide the task into an arbitrary number of groups, then we perform this partition recursively. First we find the intermediate input / output inter-far with respect to the initial input and output. Then we find the second intermediate input / output inter-far to the first three, and so on.
It is obvious that with the number of groups equal to N, the intermediate inputs / outputs of these groups will coincide with the initial nodes. Thus, we found the only correct division of all nodes into groups.
You can experiment with grouping here (Object Pascal source codes are attached).
To create a traveling salesman task, enter the number of nodes and press Enter. Or load the task from the file.
By moving the slider you can observe the principle of splitting into groups. The “Link groups” button connects the current groups by the optimal route by brute force. The “Link nodes” button connects all nodes by the optimal route by brute force. Therefore, you should not press these buttons with a large (> 18) number of nodes or groups.
Here you can download the program and source codes for solving the traveling salesman problem according to the algorithm described above.
Management bodies:
Button “Load” loads task from file with * .txt extension
The format of the txt file is as follows: in each line, after 1 space, the x and y coordinates for each node in the task are indicated. The first line contains the coordinates of the input node. In the last line - the coordinates of the output node. The remaining nodes between them in random order. Coordinates are in the range of 0-1 with an accuracy of 6 decimal places. The separator of the whole and fractional part is a comma.
The “Generate” button generates a random traveling salesman task, with the number of nodes specified in the “Nodes” field.
The “Save” button saves the coordinates of the nodes of this task.
The “Solve” button solves the traveling salesman problem, recursively breaking it into a constant number of groups specified in the “Groups” field. If the specified number of groups is greater than or equal to the number of nodes, then, naturally, a complete search of nodes will be performed. Therefore, it is not recommended to indicate the number of groups more than 18.
In this program, the division into groups is not optimal, so the intersections happen. But this disadvantage is fundamentally eliminated.
To improve the algorithm, the Nodes parameter should be divided into two independent parameters:
Nmax - the maximum number of nodes for which a complete enumeration is done without splitting into groups.
Gmax - the number of groups for splitting nodes, the number of which exceeded Nmax. And this number can be set differently. You can divide the number of nodes by a constant, you can subtract 1 from the current number of nodes, you can divide the number of nodes in the ratio of the "golden section", you can take a fixed percentage. In this regard, I conducted research.
In this program, for simplicity and clarity, Gmax = Nmax = Groups.
The program calculates one thousand nodes with Groups = 13 in less than 5 seconds. For a complete search, the result is very good.
Given N nodes located on the plane. An input node (Bx) and output node (Out) are specified. You must discover the shortest path that encompasses all nodes, starting at the input node, ending at the output node, and passing through each node only once.
There are opinions that the task of a traveling salesman can be formulated in two more ways:
1. It is necessary to discover the shortest Hamiltonian cycle.
2. It is necessary to find the shortest path starting at a given node.
However, both of these formulations on closer examination turn out to be special cases of the original formulation.
Formulation 1 implies that the input node can be any node, and the output - one of the closest to it. That requires a complete search of all the closest nodes to a randomly selected node.
Formulation 2 implies that the input node is defined, and the output node can be any. What requires a complete enumeration of all output nodes, followed by the selection of the shortest path of all the shortest.
Therefore, we will focus on the original formulation, and we will solve the problem in a general form.
It is generally recognized that the traveling salesman problem in general is guaranteed to be solved optimally only by exhaustive search of all the options.
In the algorithmic implementation of the complete iteration, it is possible to use two conditions that reduce the iteration time and cut off the obviously non-optimal paths, namely:
1. When constructing the next version of the path, calculate its length and if this length exceeds the local minimum of the length already found, skip this variant and all those it generates.
2. If the next selected edge intersects one of the previously constructed edges - skip this option and all those that it generates.
')
The last condition actually prohibits cycles, since if we imagine ourselves in the place of a real traveling salesman, then the intersection of the ribs (despite the fact that in the task it is forbidden to explicitly reuse the nodes) will actually mean the return of the traveling salesman to the place where he was already, which contradicts the definition of the optimal (shortest) of the way.
The optimal solution to the traveling salesman problem on desktops is possible. However, with an increase in the number of nodes, the time spent on a complete search increases exponentially. Thus, on a machine with a quad core processor 2.67 GHz, 10 nodes are calculated on average in 5 milliseconds, 20 nodes in 15 minutes, and calculating the optimal path for 60 nodes will take more than 6 trillion years ...
To circumvent this obstacle, people simply refuse to obtain an optimal solution for large N and instead of the traveling salesman problem they solve some other, very similar, similar problem. Such a method of substitution of the problem is called the “heuristic solution”, although heuristics in each case is no more than a randomly chosen analogy. For example, annealing is a solution to a problem by simulating the cooling of crystallizing substances, a greedy algorithm is an imitation of the behavior of a greedy person, there are methods built by analogy with the behavior of ants, an inflating balloon, etc.
The method of analogy is bad because the full search, as the best solution, is completely discarded and completely replaced by some other method. I believe that it is impossible to do so with scorn with complete enumeration, because this is the only method that is guaranteed to give the correct solution to the problem.
We will try to solve the traveling salesman problem only by complete brute force, replacing it with something else only where it is really necessary for reasons of time.
We will not look for an analogy at random, we will try to solve the traveling salesman’s problem as impartially as possible, without invoking extraneous analogies for help. Let's try to solve a common problem in general. And for this we will call for help only one analogy - an analogy with intelligence in general. How does the human intellect solve complex problems (including the traveling salesman problem)? It splits the original problem into a tree of simpler sub-problems, solves them in the reverse order and gets the result. We will do the same!
It is quite obvious that to simplify the traveling salesman problem in order to solve it by complete brute force in an acceptable time can only be done in one way — by reducing the number of nodes being sorted. And this can also be done in only one way - to merge nodes into groups - over-nodes, over-tasks (sub-tasks).
To set the traveling salesman problem recursively try to look at it recursively.
The main element in this task is a node that contains one edge and one edge:

Without invoking extraneous analogies, we immediately notice the analogy with the very formulation of the general problem, in which two “extreme” nodes are set: Bx , which includes the traveling salesman at the start, and Exit , from which the salesman leaves at the finish. We can say that the entire set of nodes N in the problem is one large node, in which the traveling salesman enters and leaves by an edge:

Thus, a general view of the recursive algorithm appears.
1. Set the nodes N.
2. Set the maximum allowable time for solving the problem Tmax.
3. Carry out a benchmark on this machine and determine the dependence of the solution time on the number of nodes with a full search of T (N) options.
4. Based on a given number of nodes N, Tmax and dependencies for T, determine how many groups (over-nodes) a set of N nodes should be split. Or set this number of nodes manually (this is exactly what we will do).
5. Split a set of N nodes into M groups.
6. Perform a complete search for M groups and find the shortest way to connect these groups.
7. After step 6, we have an entry and exit for each group, so we recursively set the salesman problem for each group, i.e. go to step 4, where N is equal to the number of nodes in each group.
8. After exiting recursion, we obtain a suboptimal path for this machine and this Tmax (or a specified number of nodes in the group).
Paragraph 4 is needed so that we do not degrade the algorithm beyond what is necessary. If the machine can perform a complete search for a given number of nodes, then we should allow it to it.
In step 5, it is obviously better to prefer M as much as possible. When M tends to N, we get an ever more accurate solution. The less we move away from complete enumeration, the more accurate our decision. It is possible to choose M according to the table made up of the simplest rough assumption that at each recursion step we will divide the sub-task into groups with the same number of nodes in the group.

As can be seen from the table, already with 18 nodes in one group, we can process more than 10 billion nodes with a recursion depth of up to 8.
If we want to improve the route found in this way, then we have the following options:
- choose a more productive machine
- increase the allowable time Tmax
- increase the number of groups
- increase recursion nesting. That is, in step 6, it is necessary to split the task into substantially (depending on N) a larger number of groups, but it is not optimal, but to subselect them, but suboptimally. For example, to divide a task from 1000 nodes into 500 groups, but not to search for the shortest way of connecting them by complete brute force (this is too long), but to break groups into sub-groups, for example, into 250 groups and search for a suboptimal path among them. And so on, until we go down to a level where the machine can do a complete bust.
How to combine nodes into groups?
In order not to attract abstract analogies and not to use vague heuristics, we will try to find the answer in the problem itself. It is absolutely clear that initially in the problem we have one group, for which the Bx and Out are set.
To break this task into at least two, we need to allocate among all nodes an intermediate node, which will become an intermediate input / output.
Since we use the Euclidean distance as a sign of optimality in the problem, to detect the new intermediate input / output we need to enter a certain limit on the distance from each node to the already existing input and output. Since we do not know what the limit is, let us mentally take it so large that it turns out that all nodes belong only to the initial group. Now mentally we will gradually reduce this limit. At the same time, one of the nodes that previously belonged to the original group should stand out from it. Regardless of what exactly we take as a limit, this node will be the node that is located at the farthest distance from the initial entry and exit. Therefore, instead of inventing the formula of the limit, we can immediately take the most distant node. After we have found this intermediate entry / exit, we must divide all the remaining nodes between the new two groups so as to ensure that the edges do not intersect.
If we need to divide the task into an arbitrary number of groups, then we perform this partition recursively. First we find the intermediate input / output inter-far with respect to the initial input and output. Then we find the second intermediate input / output inter-far to the first three, and so on.
It is obvious that with the number of groups equal to N, the intermediate inputs / outputs of these groups will coincide with the initial nodes. Thus, we found the only correct division of all nodes into groups.
You can experiment with grouping here (Object Pascal source codes are attached).
To create a traveling salesman task, enter the number of nodes and press Enter. Or load the task from the file.
By moving the slider you can observe the principle of splitting into groups. The “Link groups” button connects the current groups by the optimal route by brute force. The “Link nodes” button connects all nodes by the optimal route by brute force. Therefore, you should not press these buttons with a large (> 18) number of nodes or groups.
Here you can download the program and source codes for solving the traveling salesman problem according to the algorithm described above.
Management bodies:
Button “Load” loads task from file with * .txt extension
The format of the txt file is as follows: in each line, after 1 space, the x and y coordinates for each node in the task are indicated. The first line contains the coordinates of the input node. In the last line - the coordinates of the output node. The remaining nodes between them in random order. Coordinates are in the range of 0-1 with an accuracy of 6 decimal places. The separator of the whole and fractional part is a comma.
The “Generate” button generates a random traveling salesman task, with the number of nodes specified in the “Nodes” field.
The “Save” button saves the coordinates of the nodes of this task.
The “Solve” button solves the traveling salesman problem, recursively breaking it into a constant number of groups specified in the “Groups” field. If the specified number of groups is greater than or equal to the number of nodes, then, naturally, a complete search of nodes will be performed. Therefore, it is not recommended to indicate the number of groups more than 18.
In this program, the division into groups is not optimal, so the intersections happen. But this disadvantage is fundamentally eliminated.
To improve the algorithm, the Nodes parameter should be divided into two independent parameters:
Nmax - the maximum number of nodes for which a complete enumeration is done without splitting into groups.
Gmax - the number of groups for splitting nodes, the number of which exceeded Nmax. And this number can be set differently. You can divide the number of nodes by a constant, you can subtract 1 from the current number of nodes, you can divide the number of nodes in the ratio of the "golden section", you can take a fixed percentage. In this regard, I conducted research.
In this program, for simplicity and clarity, Gmax = Nmax = Groups.
The program calculates one thousand nodes with Groups = 13 in less than 5 seconds. For a complete search, the result is very good.
Source: https://habr.com/ru/post/151151/
All Articles