Accelerate node.js: native modules and CUDA
Sometimes developers of various web projects are faced with the need to process large amounts of data or use a resource-intensive algorithm. Older tools no longer provide the necessary performance, you have to rent / buy additional computing power, which pushes you to rewrite the slow parts of the code in C ++ or other fast languages.
In this article I will discuss how you can try to speed up the work of Node.JS (which in itself is considered to be quite fast). It's about native extensions written with C ++.
So, you have a web server on Node.JS and you received a task with a resource-intensive algorithm. To accomplish the task, it was decided to write a module in C ++. Now we need to deal with what it is - a native extension.
Node.JS architecture allows you to connect modules packaged in libraries. For these libraries js-wrappers are created with which you can call the functions of these modules directly from your server's js-code. Many standard Node.JS modules are written in C ++, but this does not prevent us from using them with such convenience, as if they were written in javascript itself. You can pass any parameters into your extension, catch exceptions, execute any code, and return the processed data back.
In the course of the article, we will understand how to create native extensions and perform several performance tests. For tests, let's take a non-complicated, but resource-intensive algorithm, which we will execute in js and in C ++. For example - we calculate the double integral.
')
Take the function:
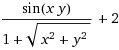
This function sets the following surface:
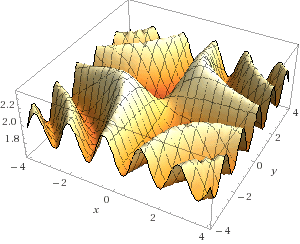
To find the double integral, we need to find the volume of the figure bounded by this surface. To do this, divide the shape into a set of parallelepipeds, with a height equal to the value of the function. The sum of their volumes will give us the volume of the whole figure and the numerical value of the integral itself. To find the volume of each parallelepiped, we divide the area under the figure into many small rectangles, then multiply their area by the value of our function in points at the edges of these rectangles. The more parallelepipeds, the higher the accuracy.
The js code that does this integration and shows us the execution time:
Now we will perform all the same operations on C ++. Personally, I used Microsoft Visual Studio 2010. First we need to download the source code for Node.JS. Go to the official website and pull up the latest version of the source. In the source folder is the file vcbuild.bat, which creates the necessary projects for Visual Studio and configs. The installed Python is required for the batch file to work. If you do not have it - we put off the off site . We set the paths to python in the Path environment variable (for Python 2.7, these will be C: \ Python27; C: \ Python27 \ Scripts). Run the batch file, get the necessary files. Next, create the .cpp file of our module. Further we write the description of our module in json-format:
Save as binding.gyp and set the utility on it, which we install using npm. This utility creates a properly configured vcxproj studio file for windows or a linux makefile. Just one comrade was created batch file, even more simplifies setting up and creating a project for the studio. You can take from him, along with an example helloworld-module . Edit the file, run the batch file - get the ready .node module. You can create a Visual Studio project manually and also manually enter all the settings - set the paths to the libs and headers, node.js, configuration type set to .dll, the target extension is .node.
Everything is set up, start writing the code.
In the .cpp file, we must declare the class inherited from ObjectWrap. All methods of this class must be static.
There must be an initialization function that we drive into the NODE_MODULE macro. In the initialization function using the NODE_SET_PROTOTYPE_METHOD macro, we specify the methods that will be available from Node.JS. We can receive the passed parameters, check their number and types and, if necessary, throw exceptions. A detailed description of all the necessary things to create an extension you can find here.
Compiling this code we get a .node file (a regular DLL with a different extension) that can be connected to our Node.JS project. The file contains the prototype of the jative object NativeIntegrator, which has an integrateNative method. Let's connect the received module:
Add this code to the already finished project on Node.JS, call the functions, compare:
We get the result:
JS result = 127.99999736028109
JS time = 127
Native result = 127.999997
Native time = 103
The difference is minimal. Increase the number of iterations on axes by 8 times. We obtain the following results:
JS result = 127.99999995875444
JS time = 6952
Native result = 128.000000
Native time = 6658
The result is surprising. We have received almost no winnings. The result on Node.JS is obtained almost exactly the same as that obtained on pure C ++. We guessed that the V8 is a fast engine, but so much so ... Yes, even purely mathematical operations can be written in pure js. We will lose a little from this, if we lose anything at all. To get the benefits of native expansion, we need to use low-level optimization. But it will be too much. The performance gain from the native module does not always pay back the cost of writing a sishnogo or even assembly code. What to do? The first thing that comes to mind is the use of openmp or native streams to solve the problem in parallel. This will speed up the solution of each individual task, but will not increase the number of tasks solved per unit of time. So this solution is not for everyone. The load on the server will not decrease. Perhaps we will also get a win when working with large amounts of memory - Node.JS will still have additional overhead and the total occupied memory will be more. But memory is now far from being as critical as CPU time. What conclusions can we draw from this study?
But let's try to speed up the work of our code? Since we have access from the native extension to anything, that is, access to the video card. We use CUDA!
For this we need the CUDA SDK, which can be found on the Nvidia website . I will not talk here about the installation and configuration, for this, and so there are many manuals. After installing the SDK, we need to make some changes to the project - rename the source from .cpp to .cu. Add CUDA support to build settings. Add the necessary dependencies to the CUDA compiler settings. Here is the new extension code, with comments on changes and additions:
Write a handler on js:
Let's start testing on the following data:
Get the results:
JS result = 127.99999736028109
JS time = 119
Native result = 127.999997
Native time = 122
CUDA result = 127.999997
CUDA time = 17
As we see, the handler on the video card already shows a strong lead. And this is despite the fact that I summarized the results of the work of each video card stream on the CPU. If you write an algorithm that runs entirely on the GPU, without using a central processor, the performance gain will be even more tangible.
We test on the following data:
We get the result:
JS result = 127.99999998968899
JS time = 25401
Native result = 128.000000
Native time = 28405
CUDA result = 128.000000
CUDA time = 3568
As we can see, the difference is huge. An optimized algorithm at CUDA would give us a performance difference of more than an order of magnitude. (And the C ++ code on this test even fell behind Node.JS in performance).
The situation considered by us is rather exotic. Resource-intensive computing on a web server with Node.JS, which is installed on a machine with a video card that supports CUDA technology. This is not often seen. But if you ever have to deal with such a thing - you know, such things are real. In fact, you can embed any piece that you can write in C ++ into your Node.JS server. That is, anything.
In this article I will discuss how you can try to speed up the work of Node.JS (which in itself is considered to be quite fast). It's about native extensions written with C ++.
Briefly about extensions
So, you have a web server on Node.JS and you received a task with a resource-intensive algorithm. To accomplish the task, it was decided to write a module in C ++. Now we need to deal with what it is - a native extension.
Node.JS architecture allows you to connect modules packaged in libraries. For these libraries js-wrappers are created with which you can call the functions of these modules directly from your server's js-code. Many standard Node.JS modules are written in C ++, but this does not prevent us from using them with such convenience, as if they were written in javascript itself. You can pass any parameters into your extension, catch exceptions, execute any code, and return the processed data back.
In the course of the article, we will understand how to create native extensions and perform several performance tests. For tests, let's take a non-complicated, but resource-intensive algorithm, which we will execute in js and in C ++. For example - we calculate the double integral.
')
What to count?
Take the function:
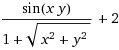
This function sets the following surface:

To find the double integral, we need to find the volume of the figure bounded by this surface. To do this, divide the shape into a set of parallelepipeds, with a height equal to the value of the function. The sum of their volumes will give us the volume of the whole figure and the numerical value of the integral itself. To find the volume of each parallelepiped, we divide the area under the figure into many small rectangles, then multiply their area by the value of our function in points at the edges of these rectangles. The more parallelepipeds, the higher the accuracy.
The js code that does this integration and shows us the execution time:
var func = function(x,y){ return Math.sin(x*y)/(1+Math.sqrt(x*x+y*y))+2; } function integrateJS(x0,xN,y0,yN,iterations){ var result=0; var time = new Date().getTime(); for (var i = 0; i < iterations; i++){ for (var j = 0; j < iterations; j++){ // var x = x0 + (xN - x0) / iterations * i; var y = y0 + (yN - y0) / iterations * j; var value = func(x, y); // // result+=value*(xN-x0)*(yN-y0)/(iterations*iterations); } } console.log("JS result = "+result); console.log("JS time = "+(new Date().getTime() - time)); } Preparing to write an extension
Now we will perform all the same operations on C ++. Personally, I used Microsoft Visual Studio 2010. First we need to download the source code for Node.JS. Go to the official website and pull up the latest version of the source. In the source folder is the file vcbuild.bat, which creates the necessary projects for Visual Studio and configs. The installed Python is required for the batch file to work. If you do not have it - we put off the off site . We set the paths to python in the Path environment variable (for Python 2.7, these will be C: \ Python27; C: \ Python27 \ Scripts). Run the batch file, get the necessary files. Next, create the .cpp file of our module. Further we write the description of our module in json-format:
{ "targets": [ { "target_name": "funcIntegrate", "sources": [ "funcIntegrate.cpp" ] } ] } Save as binding.gyp and set the utility on it, which we install using npm. This utility creates a properly configured vcxproj studio file for windows or a linux makefile. Just one comrade was created batch file, even more simplifies setting up and creating a project for the studio. You can take from him, along with an example helloworld-module . Edit the file, run the batch file - get the ready .node module. You can create a Visual Studio project manually and also manually enter all the settings - set the paths to the libs and headers, node.js, configuration type set to .dll, the target extension is .node.
Native extension
Everything is set up, start writing the code.
In the .cpp file, we must declare the class inherited from ObjectWrap. All methods of this class must be static.
There must be an initialization function that we drive into the NODE_MODULE macro. In the initialization function using the NODE_SET_PROTOTYPE_METHOD macro, we specify the methods that will be available from Node.JS. We can receive the passed parameters, check their number and types and, if necessary, throw exceptions. A detailed description of all the necessary things to create an extension you can find here.
Code
#include <node.h> // #include <v8.h> #include <math.h> using namespace node; using namespace v8; //, js float func(float x, float y){ return sin(x*y)/(1+sqrt(x*x+y*y))+2; } char* funcCPU(float x0, float xn, float y0, float yn, int iterations){ double x,y,value,result; result=0; for (int i = 0; i < iterations; i++){ for (int j = 0; j < iterations; j++){ x = x0 + (xn - x0) / iterations * i; y = y0 + (yn - y0) / iterations * j; value = func(x, y); result+=value*(xn-x0)*(yn-y0)/(iterations*iterations); } } char *c = new char[20]; sprintf(c,"%f",result); return c; } // , ObjectWrap class funcIntegrate: ObjectWrap{ public: //. static static void Init(Handle<Object> target){ HandleScope scope; Local<FunctionTemplate> t = FunctionTemplate::New(New); Persistent<FunctionTemplate> s_ct = Persistent<FunctionTemplate>::New(t); s_ct->InstanceTemplate()->SetInternalFieldCount(1); // javascript s_ct->SetClassName(String::NewSymbol("NativeIntegrator")); //, javasript NODE_SET_PROTOTYPE_METHOD(s_ct, "integrateNative", integrateNative); target->Set(String::NewSymbol("NativeIntegrator"),s_ct->GetFunction()); } funcIntegrate(){ } ~funcIntegrate(){ } // Node.JS new static Handle<Value> New(const Arguments& args){ HandleScope scope; funcIntegrate* hw = new funcIntegrate(); hw->Wrap(args.This()); return args.This(); } // , javasript static Handle<Value> integrateNative(const Arguments& args){ HandleScope scope; funcIntegrate* hw = ObjectWrap::Unwrap<funcIntegrate>(args.This()); // args, double funcCPU. // Local<String> result = String::New(funcCPU(args[0]->NumberValue(),args[1]->NumberValue(),args[2]->NumberValue(),args[3]->NumberValue(),args[4]->NumberValue())); return scope.Close(result); } }; extern "C" { static void init (Handle<Object> target){ funcIntegrate::Init(target); } NODE_MODULE(funcIntegrate, init); }; Compiling this code we get a .node file (a regular DLL with a different extension) that can be connected to our Node.JS project. The file contains the prototype of the jative object NativeIntegrator, which has an integrateNative method. Let's connect the received module:
var funcIntegrateNative = require("./build/funcIntegrate.node"); nativeIntegrator = new funcIntegrateNative.NativeIntegrator(); function integrateNative(x0,xN,y0,yN,iterations){ var time = new Date().getTime(); result=nativeIntegrator.integrateNative(x0,xN,y0,yN,iterations); console.log("Native result = "+result); console.log("Native time = "+(new Date().getTime() - time)); } Add this code to the already finished project on Node.JS, call the functions, compare:
function main(){ integrateJS(-4,4,-4,4,1024); integrateNative(-4,4,-4,4,1024); } main(); We get the result:
JS result = 127.99999736028109
JS time = 127
Native result = 127.999997
Native time = 103
The difference is minimal. Increase the number of iterations on axes by 8 times. We obtain the following results:
JS result = 127.99999995875444
JS time = 6952
Native result = 128.000000
Native time = 6658
findings
The result is surprising. We have received almost no winnings. The result on Node.JS is obtained almost exactly the same as that obtained on pure C ++. We guessed that the V8 is a fast engine, but so much so ... Yes, even purely mathematical operations can be written in pure js. We will lose a little from this, if we lose anything at all. To get the benefits of native expansion, we need to use low-level optimization. But it will be too much. The performance gain from the native module does not always pay back the cost of writing a sishnogo or even assembly code. What to do? The first thing that comes to mind is the use of openmp or native streams to solve the problem in parallel. This will speed up the solution of each individual task, but will not increase the number of tasks solved per unit of time. So this solution is not for everyone. The load on the server will not decrease. Perhaps we will also get a win when working with large amounts of memory - Node.JS will still have additional overhead and the total occupied memory will be more. But memory is now far from being as critical as CPU time. What conclusions can we draw from this study?
- Node.JS is really very fast. If you do not know how to write high-quality C ++ code with low-level optimization, then there is no point in trying to write a native extension to speed up performance. You just get extra problems.
- Use native extensions where you really need it — for example, where you need access to some system API that is not in Node.JS.
We need to go deeper
But let's try to speed up the work of our code? Since we have access from the native extension to anything, that is, access to the video card. We use CUDA!
For this we need the CUDA SDK, which can be found on the Nvidia website . I will not talk here about the installation and configuration, for this, and so there are many manuals. After installing the SDK, we need to make some changes to the project - rename the source from .cpp to .cu. Add CUDA support to build settings. Add the necessary dependencies to the CUDA compiler settings. Here is the new extension code, with comments on changes and additions:
Code
#include <node.h> #include <v8.h> #include <math.h> #include <cuda_runtime.h> // CUDA using namespace node; using namespace v8; // __device__ __host__ // CPU, GPU. __device__ __host__ float func(float x, float y){ return sin(x*y)/(1+sqrt(x*x+y*y))+2; } //__global__ - CPU, GPU __global__ void funcGPU(float x0, float xn, float y0, float yn, float *result){ float x = x0 + (xn - x0) / gridDim.x * blockIdx.x; float y = y0 + (yn - y0) / blockDim.x * threadIdx.x ; float value = func(x, y); result[gridDim.x * threadIdx.x + blockIdx.x] = value*(xn-x0)*(yn-y0)/(gridDim.x*blockDim.x); } char* funcCPU(float x0, float xn, float y0, float yn, int iterations){ double x,y,value,result; result=0; for (int i = 0; i < iterations; i++){ for (int j = 0; j < iterations; j++){ x = x0 + (xn - x0) / iterations * i; y = y0 + (yn - y0) / iterations * j; value = func(x, y); result+=value*(xn-x0)*(yn-y0)/(iterations*iterations); } } char *c = new char[20]; sprintf(c,"%f",result); return c; } class funcIntegrate: ObjectWrap{ private: static dim3 gridDim; // static dim3 blockDim; static float *result; static float *resultDev; public: static void Init(Handle<Object> target){ HandleScope scope; Local<FunctionTemplate> t = FunctionTemplate::New(New); Persistent<FunctionTemplate> s_ct = Persistent<FunctionTemplate>::New(t); s_ct->InstanceTemplate()->SetInternalFieldCount(1); s_ct->SetClassName(String::NewSymbol("NativeIntegrator")); NODE_SET_PROTOTYPE_METHOD(s_ct, "integrateNative", integrate); // GPU, Node.JS NODE_SET_PROTOTYPE_METHOD(s_ct, "integrateCuda", integrateCuda); target->Set(String::NewSymbol("NativeIntegrator"),s_ct->GetFunction()); // CUDA gridDim.x = 256; blockDim.x = 256; result = new float[gridDim.x * blockDim.x]; cudaMalloc((void**) &resultDev, gridDim.x * blockDim.x * sizeof(float)); } funcIntegrate(){ } ~funcIntegrate(){ cudaFree(resultDev); } // static char* cudaIntegrate(float x0, float xn, float y0, float yn, int iterations){ cudaEvent_t start, stop; cudaEventCreate(&start); cudaEventCreate(&stop); // CPU GPU // GPU - // bCount, // GPU int bCount = iterations/gridDim.x; float bSizeX=(xn-x0)/bCount; float bSizeY=(yn-y0)/bCount; double res=0; for (int i = 0; i < bCount; i++){ for (int j = 0; j < bCount; j++){ cudaEventRecord(start, 0); // // GPU funcGPU<<<gridDim, blockDim>>>(x0+bSizeX*i, x0+bSizeX*(i+1), y0+bSizeY*j, y0+bSizeY*(j+1), resultDev); cudaEventRecord(stop, 0); cudaEventSynchronize(stop); // // GPU cudaMemcpy(result, resultDev, gridDim.x * blockDim.x * sizeof(float), cudaMemcpyDeviceToHost); // for (int k=0; k<gridDim.x * blockDim.x; k++) res+=result[k]; } } cudaEventDestroy(start); cudaEventDestroy(stop); char *c = new char[200]; sprintf(c,"%f", res); return c; } static Handle<Value> New(const Arguments& args){ HandleScope scope; funcIntegrate* hw = new funcIntegrate(); hw->Wrap(args.This()); return args.This(); } static Handle<Value> integrate(const Arguments& args){ HandleScope scope; funcIntegrate* hw = ObjectWrap::Unwrap<funcIntegrate>(args.This()); Local<String> result = String::New(funcCPU(args[0]->NumberValue(),args[1]->NumberValue(),args[2]->NumberValue(),args[3]->NumberValue(),args[4]->NumberValue())); return scope.Close(result); } // CUDA static Handle<Value> integrateCuda(const Arguments& args){ HandleScope scope; funcIntegrate* hw = ObjectWrap::Unwrap<funcIntegrate>(args.This()); Local<String> result = String::New(cudaIntegrate(args[0]->NumberValue() ,args[1]->NumberValue(),args[2]->NumberValue(),args[3]->NumberValue(),args[4]->NumberValue())); return scope.Close(result); } }; extern "C" { static void init (Handle<Object> target){ funcIntegrate::Init(target); } NODE_MODULE(funcIntegrate, init); }; dim3 funcIntegrate::blockDim; dim3 funcIntegrate::gridDim; float* funcIntegrate::result; float* funcIntegrate::resultDev; Write a handler on js:
function integrateCuda(x0,xN,y0,yN,iterations){ var time = new Date().getTime(); result=nativeIntegrator.integrateCuda(x0,xN,y0,yN,iterations); console.log("CUDA result = "+result); console.log("CUDA time = "+(new Date().getTime() - time)); } Let's start testing on the following data:
function main(){ integrateJS(-4,4,-4,4,1024); integrateNative(-4,4,-4,4,1024); integrateCuda(-4,4,-4,4,1024); } Get the results:
JS result = 127.99999736028109
JS time = 119
Native result = 127.999997
Native time = 122
CUDA result = 127.999997
CUDA time = 17
As we see, the handler on the video card already shows a strong lead. And this is despite the fact that I summarized the results of the work of each video card stream on the CPU. If you write an algorithm that runs entirely on the GPU, without using a central processor, the performance gain will be even more tangible.
We test on the following data:
integrateJS(-4,4,-4,4,1024*16); integrateNative(-4,4,-4,4,1024*16); integrateCuda(-4,4,-4,4,1024*16); We get the result:
JS result = 127.99999998968899
JS time = 25401
Native result = 128.000000
Native time = 28405
CUDA result = 128.000000
CUDA time = 3568
As we can see, the difference is huge. An optimized algorithm at CUDA would give us a performance difference of more than an order of magnitude. (And the C ++ code on this test even fell behind Node.JS in performance).
Conclusion
The situation considered by us is rather exotic. Resource-intensive computing on a web server with Node.JS, which is installed on a machine with a video card that supports CUDA technology. This is not often seen. But if you ever have to deal with such a thing - you know, such things are real. In fact, you can embed any piece that you can write in C ++ into your Node.JS server. That is, anything.
Useful links for creating native extensions
Source: https://habr.com/ru/post/151117/
All Articles