Admit it, who as a child sat for hours on end playing a game of Dandy or Segou? And who, as the game progressed, wrote down the passwords on a piece of paper or in a specially created notebook? If this is you, and since you are reading this site, then you probably have at least once the question: “how does it work?”

I will try to explain the principles of the classic mechanisms for generating passwords using examples from the games of my childhood. I apologize in advance for the fact that all the examples will be from the NES platform (yes, the one that is “Dandy”), although the subject is not limited to it. It so happened that I did not find enough motivation in myself to do a little more research and write a little more text.

Examples will be given in order from simple to complex. At first, there will be little code, but the further you go, the more difficult it is to explain the algorithms in human language and the easier it is to explain them in technical language, so don’t be hard on it.


')

Code book

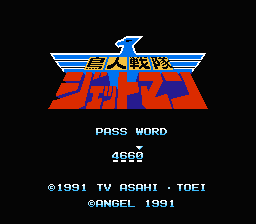
I still remember the passwords of some levels from the games of my childhood — for example, BCHK from Trolls in Crazyland (Doki! Doki! Yuuenchi), 4660 from Choujin Sentai - Jetman. It can be said that these passwords are ideal in terms of convenience: they are easy to remember and difficult to make a mistake when entering. But how much information can they contain, and what is the chance to accidentally pick up such a password?

In the first case, the alphabet of the password is 24 characters. If you count the number of combinations of characters, it will be 24 ⁴ - not so little, considering that there are only 12 levels in the game, and, in fact, besides the level number, the password does not store anything in itself. We take into account several secret passwords and calculate the probability of finding a password on one attempt: (12 + 4) / 24 ⁴ , which is equal to ~ 5.7 × 10 ^-14 . In other words, an average of 17592186044416 passwords will have to be tried before we pick up any real one.

In the second case, everything is different. Obviously, a set of 4 digits gives us exactly 10,000 (10 ⁴ ) combinations. The game contains five levels that can be completed in a different order and two levels of difficulty. Those. The password stores information about the levels and difficulty levels passed. Thus, the number of existing passwords is 2 × 2 ⁵ , i.e. 64. Hence the probability of choosing a password is 0.0064, i.e. more than half a percent. Is it enough? On average, approximately every 156th password will be correct, and given the fairly high search speed, searches will not last long. And, frankly, in childhood we often “brute force” the game, when we didn’t want to start from the very beginning.

In fact, it is senseless to evaluate the information capacity of such passwords, since they are only keys of a kind, i.e. games simply store all possible passwords, and the index of the entered password receive information about the level and so on. But for the sake of interest I will say that their theoretical capacity is 48 and 13 bits (log ₂ 24 ⁴ and log ₂ 10 ⁴ ).

And yet, how exactly are the passwords processed? In the first case, the entered password is not subjected to any transformations at all, but is simply searched for in the stored password array.


And in the second case, the game comes a bit more cunning, and first the password is converted into a binary-decimal code , which reduces its size exactly twice. This makes it possible in the game itself to reduce the size of passwords in half.

Numbers and numbers

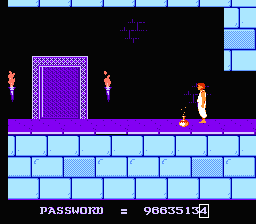I do not dare to ignore the classics: I am sure that many played in the original “Prince of Persia”, and not only on the “Dandy”. Game passwords are also sequences of decimal digits, but this time they do encode some data.

Namely, two values ​​are coded: time and level number. Because The password is 8 digits long, i.e. 100,000,000 combinations, and the game has 14 levels and 60 possible times (totaling 840 variants), it can be assumed that it is difficult to choose. But in reality this is not so, and in order to understand why, let's first examine the principle of its generation.

So, first the game creates an array of 8 elements that can store values ​​from 0 to 9. Then, two random values ​​are generated - also from 0 to 9 - and are written to this array by indices 2 and 5. These random values ​​are increments, which will be added to the saved values ​​modulo 10. This increases the number of possible passwords by 100 times, which obviously complicates the identification of patterns.

  const uint8 rand0 = rand() % 10; const uint8 rand1 = rand() % 10; char pass[8] = {0, 0, rand0, 0, 0, rand1, 0, 0}; 

Next, the level index is encoded (i.e., its minus one number): the sum of the two higher bits of the index and the second increment modulo 10 is recorded at index 7, and the sum of the two lower bits and the first increment - index 1.

  //       pass[7] = ((level >> 2) + rand1) % 10; //     pass[1] = ((level & 3) + rand0) % 10; 

It was the turn of time. It is a bit simpler with it: the sum of tens and the first increment modulo 10 is recorded at index 0, and the sum of units and the second increment at index 3. It turns out that with increments equal to zero, time is recorded in decimal digits as is. And, since the ceiling of tens is 9, then the maximum possible value of time is 99, and not an “honest” 60 minutes.

  //     pass[0] = ((time / 10) + rand0) % 10; //     pass[3] = ((time % 10) + rand1) % 10; 

Data recorded, it remains to calculate the checksum to verify the validity of the password.

  //    sum = pass[0] + pass[1] + pass[2] + pass[3]; sum += (sum % 10) + pass[5]; sum += (sum / 10) + pass[7]; //    pass[4] = sum % 10; pass[6] = sum / 10; 

For example, the legend of the password of the 13th level with the 32nd remaining minutes is “96635134”.


It becomes obvious that for selecting a password it is enough that the checksum matches the coded data. Then, if you do not take into account its specifics, you can calculate the probability to choose a password: exactly 1% (one divided by the number of possible values ​​of the sum) is quite a lot.

But this is just an ordinary amount! And for different data it may turn out the same. If you change any valid password so that the sum of the first 4 digits remains the same - it will do. What can we say about the fact that the ordinary amount of the distribution is not even, and the maximum value of this amount will never exceed 72.

Taking into account the specifics of such a sum, it turns out that with linear enumeration the probability of its coincidence with the data is very high. That is why on thematic forums in the network you can often find people's memories of how cleverly they picked up passwords for Prince of Persia.

Positional number systems

Surely many are familiar with Base64 and Base32 . By definition, these are positional number systems with bases 64 and 32, respectively. The principle is simple: we divide the bit stream into values ​​of a fixed bit length, and then, using a defined dictionary, we take the symbols as indexes by the values ​​obtained.

Many password systems are based on this principle. And the next game, on the example of which I will describe the password generation algorithm, will be Takahashi Meijin no Bouken Jima IV, in common people better known as Adventure Island 4.

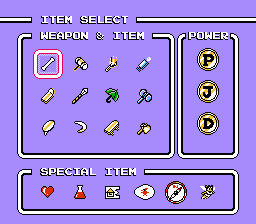The state of the game includes a set of available items (up to 12), abilities (up to 3), special items (up to 6), collected hearts (up to 8), location with an egg and information about the levels completed. But in fact, for everything except hearts and special items, one value is responsible - the progress index. This is an index in the array, where each element stores information about available items, abilities, and so on. Simply put, it is this byte that defines the set of items, abilities, and stages completed.

The first step of the algorithm is to build an array of four bytes. The value of progress is written to the first byte. Interestingly, only certain values ​​are permissible.

The second byte is recorded mask of available special items - 6 high byte bits. The remaining low 2 bits is written constant, equal to one. I guess this is the password format version. And perhaps just a constant of stricter verification of entered passwords.

The third byte is the index of the location where the egg is set (for those who did not play, a kind of checkpoint). If the egg is not set anywhere, then the value is 0xFF. The index of the location with the egg can also take only certain values ​​- there are only those locations where the egg can be installed.

And, finally, the mask of the collected hearts and half-hearts is copied to the fourth byte.

  const uint8 s_version = 1; // ... uint8 data[4] = {progress, specItems | s_version, eggLocation, hearts}; 

Then the password is encoded in the same way as Base32, but with a different alphabet: 5 bits are taken from this array in turn and written into separate bytes of an array of eight elements. In this case, using the operation "xor" is considered a checksum, which is written to the last byte of the array.

The coding table index is added to the free bits of the sixth byte. At the beginning of the game, this index is calculated randomly (value from 0 to 3), but only one will be used within one pass. Those. There may be 4 variants of the same password.

  uint8 password[8] = {}; for (var i = 0; i < 7; i++) { password[i] = takeBits(data, 5); password[7] ^= password[i]; } password[6] |= (tableIndex << 3); password[7] ^= password[6]; 

The last stage: one of the four Base32 coding tables is taken by index, and the resulting array is converted to text. Array elements are used as character indexes.

  const char* s_encodeTables[] = { "3CJV?N4Y0FP78BS1GW2QL6ZM9TR5KDXH", "JT1W9M3DV5?ZKX6GC0FB2SPHR4N8LY7Q", "R0CXM8TWB3G56PKY4FVND7QL2JZ19HS?", "8JWB3PD0?RVG5L2KX4QFZ9TN1S6MH7YC" }; char passwordStr[11] = ""; int index = 0; for (var i = 0; i < 8; i++) { passwordStr[index++] = s_encodeTables[tableIndex][password[i]]; if (i == 3 || i == 5) { passwordStr[index++] = '-'; } } 

There are 32 ⁸ possible password options. It is easy to count the number of suitable passwords - just multiply the number of valid values ​​for each of the variables being coded. So, we can encode 26 egg locations, 20 different progress values, 256 (2 ⁸ ) combinations of collected hearts, 64 (2 ⁶ ) combinations of special items and 4 password options. Total: 26 × 20 × 256 × 64 × 4 = 34078720 passwords. From here the probability to pick up the password is ~ 0.03% - we need an average of 32,264 attempts.

Graphic chaos

In some cases, developers show originality and use graphical passwords. They could be encountered, for example, in the games of the Mega Man series. Of course, the convenience of such passwords is doubtful - especially from the habit. But this is nothing compared to the long passwords in Japanese, which, alas, I did not have the strength to cover in this article.

As an example, I will take the game Power Blade 2. It uses a password consisting of 12 bonus icons located in a 4x3 grid. There are a total of 8 different icons, including an empty one. In fact, the difference between a character password and a graphic password of this kind is only in the representation of its elements, if you replace the icons with symbols, the essence will not change.

Each icon corresponds to a number from 0 to 7, in accordance with their order of appearance when the password is typed:

0	one	2	3	four	five	6	7

It is easy to calculate that we have 8 ¹² combinations, although the game saves only information about the levels completed and the costumes available. Only 5 levels (not counting the final), which can be held in random order, and 4 costumes. Those. 5 bits and 4 bits respectively, 9 bits in total. The password also has a capacity of 12 × log ₂ 8, i.e. 36 bits is more than enough.

Starting the generation of a password, the game, as usual, forms an array. At this time, immediately of the 12 elements, each of which corresponds to a password cell. Each cell has a capacity of 3 bits, and the game records 2 bits of value in them, leaving the low bit for the checksum.

  uint8 pass[12] = {}; //     pass[7] = (clearedLevelsMask & 0x3) << 1; //    pass[9] = (clearedLevelsMask & 0xC) >>> 1; //    pass[11] = (clearedLevelsMask & 0x10) >>> 2; //     pass[8] = (suitsMask & 0x3) << 1; //     pass[10] = (suitsMask & 0xC) >>> 1; 

Then a 6-bit checksum is considered, which is the arithmetic sum of all the elements of the array. This sum is then bitwise recorded in the reserved low bits of the cells.

  uint8 calcChecksum(const uint8* pass) { uint8 checksum = 0; for (int i = 0; i < 12; i++) { checksum += pass[i]; } for (int i = 0; i < 6; i++) { pass[i + 6] |= (checksum >> i) & 1; } } 

The result is something like this:


The data are prepared, the next step is a permutation of one of the 5 tables. Associated with cryptography, is not it? Depending on the mask of the levels passed, the permutation table is selected. Tables contain indices of elements in accordance with their new order.

  char s_swizzleTableFinal[] = {0, 6, 5, 4, 10, 1, 9, 3, 7, 8, 2, 11}; char s_swizzleTables[][] = { {0, 2, 3, 1, 4, 6, 9, 5, 7, 8, 10, 11}, {8, 2, 3, 6, 10, 1, 9, 5, 7, 0, 4, 11}, {5, 4, 3, 10, 6, 0, 9, 8, 7, 1, 2, 11}, {3, 4, 1, 2, 6, 5, 9, 10, 7, 8, 0, 11} }; void swizzlePassword(uint8* pass, uint8 clearedLevelsMask) { const uint8* swizzTable = (clearedLevelsMask == 0x1F) ? s_swizzleTableFinal : s_swizzleTables[clearedLevelsMask % 4]; uint8 swizzledPass[12] = {}; for (var i = 0; i < 12; i++) { swizzledPass[i] = pass[swizzTable[i]]; } for (var i = 0; i < 12; i++) { pass[i] = swizzledPass[i]; } } 

The last step is to apply the increment table. Those. each cell is summed with the corresponding element of the table modulo 8. It is precisely because of this that the icons will be different even for the same values.

  void applyIncrementTable(uint8* pass) { for (var i = 0; i < 12; i++) { pass[i] = (pass[i] + s_incrementTable[i]) % 8; } } 

Here we have a ready-made password. And it turns out that 15 bits out of 36 are used in this password. But why?

The fact is that these bits are not so unused. The password decoding procedure takes information from them about the collected L and E bonuses, as well as their current quantity, but then checks that all these values ​​are zero. Hence we can assume that it was originally planned to save this information, but then it was decided to abandon it.

Whether this is the result of gameplay balancing, or simply a disabled developer tool is unknown. Read more about it here .

Variable lengths

Somewhere at home I have a notebook, painted with passwords of the main RPG of my childhood - Little Ninja Brothers. Despite the fact that this game is nothing supernatural, it took me several years to complete. After all, it was my first RPG, and at first I didn’t even know that it was possible to “swing” there, so it took about half a year to defeat the second boss without pumping (the benefit is the opportunity to play together).

At one time, this particular game made me think about the structure of the password system - once, all the day, sitting in front of the TV, I looked for patterns in passwords and tried to determine their dependence on current characteristics. As a result, I even managed to pick up one password and increase the amount of money, but this was the only successful case.

After a while, in the process of becoming an IT specialist in me, I once remembered that incident. And, since he was very inquisitive and loved to break his head, decided during the university holidays, by all means find out the mechanism for generating passwords. Now it would be enough for me to do this, but then it took a whole week, but the goal was nevertheless achieved.

This case is more interesting than the previous ones, if only because the password has a variable length: as the game progresses, new characters are added. Moreover, the password stores much more data than in all previous ones taken together. As can be seen from the screenshot, the alphabet is 32 characters, and the maximum length of the entered password is 54 characters. This gives us 32 ⁵⁴ possible passwords of maximum length, and taking into account the variable length, there are 32 ¹ + 32 ² + ... + 32 ⁵⁴ variants. If you count the amount of information that can accommodate one password of maximum length, it will be 270 bits (log ₂ 32 ⁵⁴ ).

So, what kind of data does the password store? Since this is an RPG, there are a lot of characteristics, and almost all of them need to be saved.


In fact, not all of this data is saved, and not all stored data is listed. Not mentioned remained visited cities, the current location and a couple of bits with information about game events occurred. In turn, the level and health are not preserved, since these two quantities directly depend on the amount of experience and are redundant data. Also, the number of spetsudars of the second player is not saved, since It is essentially optional.

So how does all this work? To begin with, the game stores an array of pointers to the bytes of variables that need to be saved. According to these pointers, the game forms an array of bytes, which is then subjected to encoding. This array is divided into 4 groups of 8 bytes (6 bytes in the last group).

  const char s_groupsBytes[4] = {8, 8, 8, 6}; const char* s_passDataMap[30] = { // Group 1 &currLocation, &bells, &moneyLo, &expLo &moneyMed, &expHi, &moneyHi, &kicks, // Group 2 &visitedCitiesLo, &visitedCitiesHi, &mBonusCount, &tStarsTypes, &punch, &usedTreasures, &tStars, &treasures, // Group 3 &sword, &bombs, &shield, &skboards, &robe, &dragster, &talisman, &meatbuns, // Group 4 &amulet, &sweetbuns, &light, &batteries, &whirlyBirds, &medicine }; 

To make passwords as compact as possible, all null values ​​are ignored. To this end, for each of the four groups of the array, a mask of nonzero values ​​is compiled - one byte, where the i-th bit indicates whether the i-th element of the array should be included in the password. In a formed array, this mask will go in front of the group to which it corresponds.

  uint8 valuesMask(const uint8* data, int group) { uint8 valuesMask = 0; const int startIndex = group * 8; for (int i = startIndex + s_groupsBytes[group] - 1; i >= startIndex; i--) { valuesMask <<= 1; if (data[i] != 0) { valuesMask |= 1; } } return valuesMask; } 

The same operation at the end applies to groups in the case when all group values ​​are zero: there is a four-bit mask (4 high bits of a byte), where the i-th bit (from high to low) indicates that the password is included i-th array group. This mask will be written in the header, right in front of these groups.

In addition, there is a length table, where each byte of the array corresponds to its significant number of bits. Those. as a result, not the entire array of bytes will be encoded, but only the used bits of the values. The same technique is used for masks of nonzero values ​​- the number of mask bits used corresponds to the number of bytes in the group.

The resulting array is an analogue of the bit stack: adding variables occurs by “front substitution” - for N added bits a logical right shift to N is applied to the entire array, and the variable value is written to the bits released at the beginning.

  const char s_bitLengths[] = { 8, 7, 8, 8, 8, 8, 1, 7, 8, 2, 3, 4, 4, 2, 4, 2, 3, 4, 3, 4, 3, 1, 3, 1, 3, 4, 3, 4, 4, 1 }; void pushBits(uint8* data, uint8 value, int bitCount) { shiftRight(data, bitCount); writeBits(data, value, bitCount); } // ... uint8 encodedData[30] = {}; uint8 groupsMask = 0; for (int i = 3; i >= 0; i--) { groupsMask >>= 1; uint8 currMask = valuesMask(passData, i); if (currMask != 0) { groupsMask |= 0x80; const uint8 valuesCount = s_groupsBytes[i]; const int startIndex = i * 8; for (int j = startIndex + valuesCount - 1; j >= startIndex; j--) { if (passData[j] != 0) { pushBits(encodedData, passData[j], s_bitLengths[j]); } } pushBits(encodedData, currMask, valuesCount); } } 

Then 4 bytes are added to the beginning of the array, which are a kind of header. , — 8- 0 31, 32.

, , , . 20- , , .

  uint32 calcChecksum(uint8* data, int count) { uint32 sum = 0; for(int i = 0; i < count; i++) { sum += data[i] * (i + 1); } return sum; } // ... const uint8 increment = rand() % 32; shiftRight(encodedData, 32); encodedData[3] = increment; uint32 checksum = calcChecksum(&encodedData[3], (encodedDataBitLength + 7) / 8); encodedData[0] = checksum & 0xFF; encodedData[1] = (checksum >> 8) & 0xFF; encodedData[2] = ((checksum >> 16) & 0xF) | groupsMask; 

, , Base32. , , .

  uint8 password[54] = {}; uint8* header = encodedData; uint8* body = &encodedData[4]; // Encode header (3 bytes + increment = 6 chars) for (int i = 0; i < 5; i++) { password[i] = takeBits(header, 3, 5); } password[5] = increment; const int charCount = (((byteCount + 1) * 8 + 4) / 5) - 1; // Encode password data for (var i = 0; i < charCount; i++) { password[i + 6] = takeBits(body, byteCount, 5); } 

, , .

  // Apply increment skipping increment char for (var i = 0; i < password.length; i++) { if (i != 5) { password[i] = (password[i] + increment) % 32; } } 

, , : .

  const wchar_t* s_passwordCharTable = L"—BCD\u25a0FGH+JKLMN\u25cfPQRST\u25b2VWXYZ234567"; for (int i = 0; i < charCount; i++) { std::cout << s_passChars[password[i]]; if (i % 6 == 5) { std::cout << ' '; } } 

JavaScript
Adventure Island 4 (Takahashi Meijin no Bouken Jima IV) Power Blade 2 , Little Ninja Brothers .

, - .

Prince of Persia .

Links

• NES- CaH4e3'.
• Griever'.
• tasvideos.org.
• roman_pro .