About sorting content based on user ratings
Write this post attracted me to this article . Many people remember her from this picture.
The article touches the right topic, but from the point of view of mathematics and common sense, it is fundamentally wrong.
For those who have not read it, let me remind you: it deals with sorting content based on user ratings. The main problem is that if any article (or product) has only one score of 5 points, then its rating will be higher than that of an article with a hundred votes in five balls and one in 4 points.
The author proposes to use the formula that was written on the glass in the film “Social Network”:
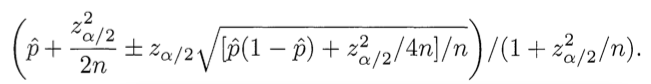
Wilson confidence interval .
This sounds, of course, seriously, but there is no reason to apply this formula to the task, except for one episode from the film, based on a tabloid novel. Confidence intervals were originally created in order to estimate the probability that the hypothesis is supported by statistics, and not for the rating. Confidence intervals depend very much on the necessary probability and the principle of its choice is not clear from the article.
')
Moreover, the author tries to apply it for a 5-point assessment, although this formula describes only the distribution with two options. For these purposes there are other formulas. If the site has a rating with a plus and a minus, then this is also not a two variant distribution. In the film, there were exactly two options - the user had only the opportunity to vote for one of the two girls, and the probability of closing the page is much lower than voting.
As a result, we are offered to sort by evaluation (up to a randomly chosen parameter) the lower limit of the likelihood that the user will put + if he does vote.
If users are shown articles with the highest rating by default and this rating depends on the number of ratings, then we have a positive inverse effect. Older articles are higher in the ranking, they get more visitors, they get more ratings as a result, they are even more divorced from younger articles.
Even if all articles are added at the same time, then due to a random evaluation, several random articles will soar upwards and gain more votes, and a chain reaction will begin again.
If the rating strongly influences the number of visits to the page, then either use both positive and negative ratings, so that bona fide users cleaned the “top”, or do not use the number of ratings as a sort parameter in any way, and to avoid inaccurate articles at the top of the rating, exclude articles with a smaller number of votes like on AG.ru.
The main advantage of such types of ratings for positive articles is the rating so it depends on the number of voters and there will be no articles with one random vote at the top. Moreover, the rating of good articles is distributed close to the binomial distribution, the behavior of which is modeled by the “formula on glass”.
Plus / minus is a good rating option. In the top there will be no bad articles and unverified. It is more intuitive for users than any mathematical modeling and is very simple to organize. The option with only a plus is worse, since the user, having seen a bad article, cannot in any way influence her position.
It is with these ratings that problems arise when, thanks to one vote, the rating of some article is not justified. The easiest way to avoid this is to exclude from the rating articles with a small number of votes.
If you do not want to exclude articles with a small number of votes, then there are many solutions to this problem, however, there is no exact answer which of them can be used. I will give the simplest of them.
Mat. waiting for a rating (the most likely value of article rating after an infinite number of votes) for an article for which no one has yet voted equals the average rating of all articles on the site.
Mat. waiting for the rating of the article for which you have already voted will be somewhere between the average rating of all articles and the average rating of this article. Moreover, with an increase in the number of votes, the rating should increasingly take into account the rating of the article itself than the average rating. The simplest formula that implements this is the arithmetic average weighted by the number of votes of the average article and the current one:

Where R is the average rating of all articles, N is the average number of votes. Ri is the average rating of this article, Ni is the number of votes of this article. R and N can be substituted by constants - they change little over time.
You can add a conservatism setting to the formula:

K> 0. The smaller the K, the easier it is for the new article to break up in the issue. The higher it is, the more stable the grading will be and the stronger the “rich get richer” effect will be. When K = 0, sorting reduces to the simplest option.
As already mentioned, our main problem is that if any article (or product) has only one score of 5 points, then its rating will be higher than the article with a hundred votes at five points and one at 4 points. In other words, voices have different weights. The only simple rating that is free from this drawback is plus / minus. However, asterisks are more familiar to users, they can be put into the delivery of Yandex and Google and they allow users to judge how good the product is (4 stars are more understandable than +40).
Therefore, you can combine two options: display "asterisks" to users, but sort them by pluses and minuses. A voice increases the score of article 1 if it is higher, say 3, or decreases by 1 if lower. It is possible to complicate a little: the voice increases the estimate by the number of points put by the user minus the average rating of articles (R - Ri).
However, in this case, the conservatism of the rating and the effect of "the rich get richer" will be higher than the version with the average-hung.
Read the second part

The article touches the right topic, but from the point of view of mathematics and common sense, it is fundamentally wrong.
For those who have not read it, let me remind you: it deals with sorting content based on user ratings. The main problem is that if any article (or product) has only one score of 5 points, then its rating will be higher than that of an article with a hundred votes in five balls and one in 4 points.

Maths
The author proposes to use the formula that was written on the glass in the film “Social Network”:
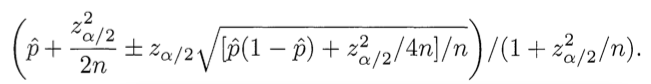
Wilson confidence interval .
This sounds, of course, seriously, but there is no reason to apply this formula to the task, except for one episode from the film, based on a tabloid novel. Confidence intervals were originally created in order to estimate the probability that the hypothesis is supported by statistics, and not for the rating. Confidence intervals depend very much on the necessary probability and the principle of its choice is not clear from the article.
')
Moreover, the author tries to apply it for a 5-point assessment, although this formula describes only the distribution with two options. For these purposes there are other formulas. If the site has a rating with a plus and a minus, then this is also not a two variant distribution. In the film, there were exactly two options - the user had only the opportunity to vote for one of the two girls, and the probability of closing the page is much lower than voting.
As a result, we are offered to sort by evaluation (up to a randomly chosen parameter) the lower limit of the likelihood that the user will put + if he does vote.
The rich get rich
If users are shown articles with the highest rating by default and this rating depends on the number of ratings, then we have a positive inverse effect. Older articles are higher in the ranking, they get more visitors, they get more ratings as a result, they are even more divorced from younger articles.
Even if all articles are added at the same time, then due to a random evaluation, several random articles will soar upwards and gain more votes, and a chain reaction will begin again.
If the rating strongly influences the number of visits to the page, then either use both positive and negative ratings, so that bona fide users cleaned the “top”, or do not use the number of ratings as a sort parameter in any way, and to avoid inaccurate articles at the top of the rating, exclude articles with a smaller number of votes like on AG.ru.
Plus / minus
The main advantage of such types of ratings for positive articles is the rating so it depends on the number of voters and there will be no articles with one random vote at the top. Moreover, the rating of good articles is distributed close to the binomial distribution, the behavior of which is modeled by the “formula on glass”.
Plus / minus is a good rating option. In the top there will be no bad articles and unverified. It is more intuitive for users than any mathematical modeling and is very simple to organize. The option with only a plus is worse, since the user, having seen a bad article, cannot in any way influence her position.
"Five Stars"
It is with these ratings that problems arise when, thanks to one vote, the rating of some article is not justified. The easiest way to avoid this is to exclude from the rating articles with a small number of votes.
If you do not want to exclude articles with a small number of votes, then there are many solutions to this problem, however, there is no exact answer which of them can be used. I will give the simplest of them.
Mat. waiting for a rating (the most likely value of article rating after an infinite number of votes) for an article for which no one has yet voted equals the average rating of all articles on the site.
Mat. waiting for the rating of the article for which you have already voted will be somewhere between the average rating of all articles and the average rating of this article. Moreover, with an increase in the number of votes, the rating should increasingly take into account the rating of the article itself than the average rating. The simplest formula that implements this is the arithmetic average weighted by the number of votes of the average article and the current one:
Where R is the average rating of all articles, N is the average number of votes. Ri is the average rating of this article, Ni is the number of votes of this article. R and N can be substituted by constants - they change little over time.
You can add a conservatism setting to the formula:
K> 0. The smaller the K, the easier it is for the new article to break up in the issue. The higher it is, the more stable the grading will be and the stronger the “rich get richer” effect will be. When K = 0, sorting reduces to the simplest option.
Combined rating
As already mentioned, our main problem is that if any article (or product) has only one score of 5 points, then its rating will be higher than the article with a hundred votes at five points and one at 4 points. In other words, voices have different weights. The only simple rating that is free from this drawback is plus / minus. However, asterisks are more familiar to users, they can be put into the delivery of Yandex and Google and they allow users to judge how good the product is (4 stars are more understandable than +40).
Therefore, you can combine two options: display "asterisks" to users, but sort them by pluses and minuses. A voice increases the score of article 1 if it is higher, say 3, or decreases by 1 if lower. It is possible to complicate a little: the voice increases the estimate by the number of points put by the user minus the average rating of articles (R - Ri).
However, in this case, the conservatism of the rating and the effect of "the rich get richer" will be higher than the version with the average-hung.
Read the second part
Source: https://habr.com/ru/post/150683/
All Articles