Collaborative filtering
In today's world, one often encounters the problem of recommending goods or services to users of an information system. In the old days, for the formation of recommendations, a summary of the most popular products was treated: this can be observed even now by opening the same Google Play . But over time, such recommendations began to be supplanted by targeted (targeted) offers: users are recommended not just popular products, but those products that will surely appeal to them. Not so long ago, Netflix held a contest with a prize fund of $ 1 million, the task of which was to improve the algorithm for recommending films ( more ). How do these algorithms work?
This article discusses the algorithm for collaborative filtering by user similarity, determined using a cosine measure, and its implementation in python.

Suppose we have a matrix of user ratings for products, for simplicity, the products are assigned numbers 1-9:

')
You can set it using a csv-file, in which the first column is the user name, the second is the product identifier, and the third is the user rating. Thus, we need a csv file with the following contents:
To begin with, we will develop a function that will read the above csv file. For the storage of recommendations, we will use the standard for python data structure dict: each user is assigned a reference book of his ratings of the type “product”: “rating”. The result is the following code:
It is intuitively clear that in order to recommend the user # 1 of a product, you need to choose from products that some users like 2-3-4-etc., Who are most similar in their estimates to user # 1. How to get the numerical expression of this "similarity" of users? Suppose we have M products. Estimates given by a single user represent a vector in the M-dimensional product space, and we can compare vectors. Among the possible measures are the following:
I will discuss the various measures and aspects of their application in more detail in a separate article. For now, suffice it to say that in recommender systems the cosine measure and the Tanimoto correlation coefficient are most often used. Let us consider in more detail the cosine measure, which we are going to implement. The cosine measure for two vectors is the cosine of the angle between them. From the school mathematics course, we remember that the cosine of the angle between two vectors is their scalar product divided by the length of each of the two vectors:
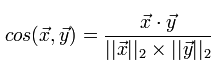
We implement the calculation of this measure, not forgetting that we have a lot of user ratings presented in the form of dict "product": "assessment"
The implementation used the fact that the scalar product of the vector itself gives itself the square of the length of the vector - this is not the best solution in terms of performance, but in our example, the speed of work is not critical.
So, we have a user preferences matrix and we can determine how two users resemble each other. Now it remains to implement the algorithm of collaborative filtering, which consists of the following:
As a formula, this algorithm can be represented as
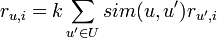
where sim is the chosen measure of similarity between two users, U is the set of users, r is the mark, k is the normalization factor:
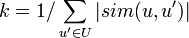
Now you just have to write the corresponding code
To check its performance, you can run the following command:
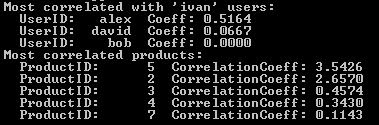
That will lead to the following result:
We looked at an example and implemented one of the simplest options for collaborative filtering using a cosine measure of similarity. It is important to understand that there are other approaches to collaborative filtering, other formulas for calculating product ratings, other measures of similarity ( article , section "See also"). Further development of this idea can be carried out in the following directions:
This article discusses the algorithm for collaborative filtering by user similarity, determined using a cosine measure, and its implementation in python.

Input data
Suppose we have a matrix of user ratings for products, for simplicity, the products are assigned numbers 1-9:

')
You can set it using a csv-file, in which the first column is the user name, the second is the product identifier, and the third is the user rating. Thus, we need a csv file with the following contents:
alex,1,5.0 alex,2,3.0 alex,5,4.0 ivan,1,4.0 ivan,6,1.0 ivan,8,2.0 ivan,9,3.0 bob,2,5.0 bob,3,5.0 david,3,4.0 david,4,3.0 david,6,2.0 david,7,1.0 To begin with, we will develop a function that will read the above csv file. For the storage of recommendations, we will use the standard for python data structure dict: each user is assigned a reference book of his ratings of the type “product”: “rating”. The result is the following code:
import csv def ReadFile (filename = "<csv_file_location>"): f = open (filename) r = csv.reader (f) mentions = dict() for line in r: user = line[0] product = line[1] rate = float(line[2]) if not user in mentions: mentions[user] = dict() mentions[user][product] = rate f.close() return mentions Measure of similarity
It is intuitively clear that in order to recommend the user # 1 of a product, you need to choose from products that some users like 2-3-4-etc., Who are most similar in their estimates to user # 1. How to get the numerical expression of this "similarity" of users? Suppose we have M products. Estimates given by a single user represent a vector in the M-dimensional product space, and we can compare vectors. Among the possible measures are the following:
- Cosine measure
- Pearson Correlation Coefficient
- Euclidean distance
- Tanimoto coefficient
- Manhattan distance, etc.
I will discuss the various measures and aspects of their application in more detail in a separate article. For now, suffice it to say that in recommender systems the cosine measure and the Tanimoto correlation coefficient are most often used. Let us consider in more detail the cosine measure, which we are going to implement. The cosine measure for two vectors is the cosine of the angle between them. From the school mathematics course, we remember that the cosine of the angle between two vectors is their scalar product divided by the length of each of the two vectors:
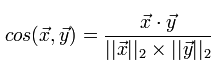
We implement the calculation of this measure, not forgetting that we have a lot of user ratings presented in the form of dict "product": "assessment"
def distCosine (vecA, vecB): def dotProduct (vecA, vecB): d = 0.0 for dim in vecA: if dim in vecB: d += vecA[dim]*vecB[dim] return d return dotProduct (vecA,vecB) / math.sqrt(dotProduct(vecA,vecA)) / math.sqrt(dotProduct(vecB,vecB)) The implementation used the fact that the scalar product of the vector itself gives itself the square of the length of the vector - this is not the best solution in terms of performance, but in our example, the speed of work is not critical.
Algorithm of collaborative filtering
So, we have a user preferences matrix and we can determine how two users resemble each other. Now it remains to implement the algorithm of collaborative filtering, which consists of the following:
- Select L users whose tastes are most similar to the tastes in question. To do this, for each of the users, you need to calculate the selected measure (in our case, the cosine) with respect to the user in question, and select L the largest. For Ivan, from the table above, we get the following values:

- For each user, his scores will be multiplied by the calculated value of the measure, so the scores of more “similar” users will have a stronger effect on the final position of the product, which can be seen in the table in the illustration below.
- For each of the products, calculate the sum of calibrated ratings of L closest users, divide the resulting amount into the sum of measures L of selected users. The sum is shown in the illustration in the “sum” line, the final value in the “result” line
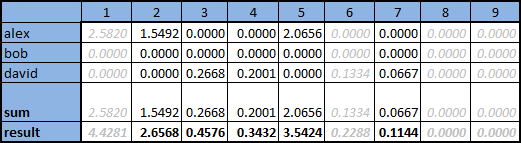
The columns of products that have already been evaluated by the user in question are marked in gray and it does not make sense to re-offer them to them.
As a formula, this algorithm can be represented as
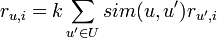
where sim is the chosen measure of similarity between two users, U is the set of users, r is the mark, k is the normalization factor:
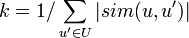
Now you just have to write the corresponding code
import math def makeRecommendation (userID, userRates, nBestUsers, nBestProducts): matches = [(u, distCosine(userRates[userID], userRates[u])) for u in userRates if u <> userID] bestMatches = sorted(matches, key=lambda(x,y):(y,x), reverse=True)[:nBestUsers] print "Most correlated with '%s' users:" % userID for line in bestMatches: print " UserID: %6s Coeff: %6.4f" % (line[0], line[1]) sim = dict() sim_all = sum([x[1] for x in bestMatches]) bestMatches = dict([x for x in bestMatches if x[1] > 0.0]) for relatedUser in bestMatches: for product in userRates[relatedUser]: if not product in userRates[userID]: if not product in sim: sim[product] = 0.0 sim[product] += userRates[relatedUser][product] * bestMatches[relatedUser] for product in sim: sim[product] /= sim_all bestProducts = sorted(sim.iteritems(), key=lambda(x,y):(y,x), reverse=True)[:nBestProducts] print "Most correlated products:" for prodInfo in bestProducts: print " ProductID: %6s CorrelationCoeff: %6.4f" % (prodInfo[0], prodInfo[1]) return [(x[0], x[1]) for x in bestProducts] To check its performance, you can run the following command:
rec = makeRecommendation ('ivan', ReadFile(), 5, 5) That will lead to the following result:

Conclusion
We looked at an example and implemented one of the simplest options for collaborative filtering using a cosine measure of similarity. It is important to understand that there are other approaches to collaborative filtering, other formulas for calculating product ratings, other measures of similarity ( article , section "See also"). Further development of this idea can be carried out in the following directions:
- Optimization of the used data structures . When storing data in python in the form of dict, every time a call is made to a specific value, a hash calculation is performed and the situation gets worse the longer the line of names. In practical tasks, sparse matrices can be used to store data, and instead of textual user names and product names, use numeric identifiers (number all users and all products)
- Performance Optimization . Obviously, to calculate the recommendation for each user request is extremely expensive. There are several ways to work around this problem:
- Clustering users and calculating the similarity measure only between users belonging to the same cluster
- Calculation of product-product similarity coefficients. To do this, you need to transpose the use-product matrix (you will get a product-user matrix), after which for each product you can calculate the set of the most similar products using the same cosine measure and remembering the k nearest ones. This is quite a laborious process, so you can produce it once in M hours / days. But now we have a list of products that are similar to this one, and multiplying the user's rating by the value of the measure of product similarity, we get the recommendation for O (N * k) , where N is the number of user ratings
- Selection of measures of similarity . The cosine measure is one of the frequently used, but the choice of measure should be made only according to the results of the analysis of the system data.
- Modification of the filtering algorithm . Perhaps a different filtering algorithm will give more accurate recommendations in a particular system. Again, the comparison of different algorithms can be made only when applied to a specific system.
Literature
Source: https://habr.com/ru/post/150399/
All Articles